Параллелограмм и ромб
Готовиться с нами - ЛЕГКО!

Биссектрисы углов \(B\) и \(C\) параллелограмма \(ABCD\) пересекаются на стороне \(AD\). Найдите \(BC\), если \(AB=4\).
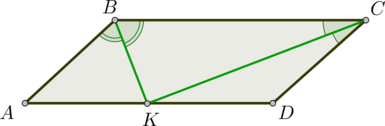
По свойству биссектрисы параллелограмма \(\triangle ABK\) и \(\triangle CDK\) – равнобедренные (\(AB=AK\), \(CD=DK\)). Следовательно, \[BC=AD=AK+DK=AB+CD=2AB=8.\]
В параллелограмме \(ABCD\) проведены биссектрисы \(AN\) и \(BE\) односторонних углов. Найдите \(BE\), если \(AN=16\), \(AB=10\).
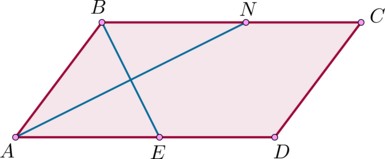
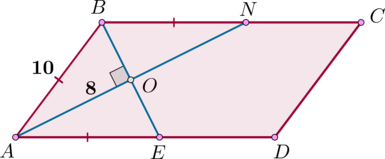
По свойству биссектрисы параллелограмма \(\triangle ABE\) и \(\triangle
ABN\) – равнобедренные, то есть \(AE=AB=BN\). Следовательно, \(AO\) – биссектриса, проведенная к основанию, значит, высота, то есть \(\angle AOB=90^\circ\), а также и медиана, то есть \(BO=OE\). Аналогично \(AO=ON=\frac12AN=8\). Тогда по теореме Пифагора из \(\triangle AOB\): \[BO=\sqrt{AB^2-AO^2}=6 \quad\Rightarrow\quad BE=2\cdot 6=12.\]
Один угол параллелограмма больше другого на \(70^\circ\). Найдите больший угол. Ответ дайте в градусах.

В параллелограмме противоположные углы равны, а прилежащие к одной стороне в сумме дают \(180^\circ\). Следовательно, пусть \(x\) – некоторый угол параллелограмма, тогда второй равен \(x+70^\circ\). Так как они не могут быть противоположными, то они прилежащие к одной стороне, следовательно, \[x+x+70^\circ=180^\circ\quad\Rightarrow\quad x=55^\circ\] Тогда больший угол параллелограмма равен \(x+70^\circ=125^\circ\).
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Проведем биссектрисы двух соседних углов. Пусть они разбили первый угол на два угла, равных \(x\), второй угол — на два угла, равных \(y\). Нужно найти \(\alpha\).
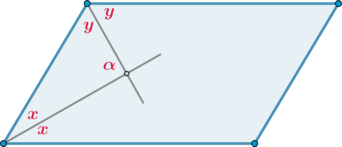
По свойству параллелограмма сумма его углов, прилежащих к одной стороне, равна \(180^\circ\). Следовательно, \(2x+2y=180^\circ\), или \(2(x+y)=180^\circ\), откуда \(x+y=90^\circ\).
Так как сумма углов в треугольнике равна \(180^\circ\), то \(x+y+\alpha=180^\circ\), откуда \(\alpha=180^\circ-(x+y)=180^\circ-90^\circ=90^\circ\).
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении \(4:3\), считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен \(88\).
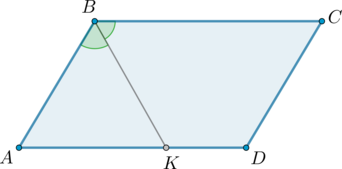
Из условия задачи следует, что \(AK:KD=4:3\). Обозначим \(AK=4x\), \(KD=3x\). Следовательно, \(AD=7x\).
Так как в параллелограмме противоположные стороны параллельны, то \(\angle AKB=\angle KBC\) как накрест лежащие при \(AD\parallel BC\) и секущей \(BK\). Следовательно, \(\angle AKB=\angle ABK\), то есть \(\triangle ABK\) равнобедренный: \(AK=AB\). Отсюда \(AB=4x\).
Следовательно, периметр \(88=2(4x+7x)\) (так как противоположные стороны параллелограмма равны), следовательно, \(x=4\).
Значит, большая сторона параллелограмма равна \(7x=28\).
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна \(5\). Найдите его большую сторону.
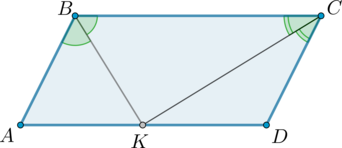
\(AB=5\). Так как в параллелограмме противоположные стороны параллельны, то \(\angle AKB=\angle KBC\) как накрест лежащие при \(AD\parallel BC\) и секущей \(BK\). Следовательно, \(\angle AKB=\angle
ABK\), то есть \(\triangle ABK\) равнобедренный: \(AK=AB\).
Аналогично \(DC=DK\).
Так как в параллелограмме противоположные стороны равны, то \(AK=AB=5=CD=DK\). Следовательно, \(AD=5+5=10\) – большая сторона.
Найдите высоту ромба, сторона которого равна \(\sqrt3\), а острый угол равен \(60^\circ\).
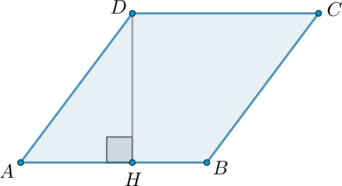
\(AD=\sqrt3\), \(\angle A=60^\circ\). Следовательно, \(\angle ADH=30^\circ\). Катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, следовательно, \(AH=0,5AD=\frac{\sqrt3}2\). Тогда по теореме Пифагора: \[DH=\sqrt{(\sqrt3)^2-\left(\dfrac{\sqrt3}2\right)^2}=\dfrac32\]



