Площади и углы трапеции (страница 2)
Готовиться с нами - ЛЕГКО!

В трапеции \(ABCD\) с основаниями \(BC = 4\) и \(AD > BC\) угол \(A\) – прямой. Известно, что \(CD = 6\), \(\angle D = 60^{\circ}\). Найдите среднюю линию трапеции \(ABCD\).
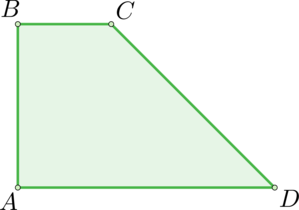
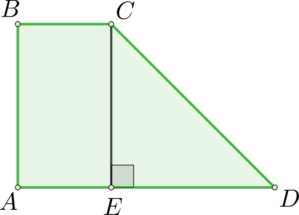
Из точки \(C\) опустим высоту \(CE\). В прямоугольном треугольнике \(CDE\): \(\angle ECD = 30^{\circ}\). В прямоугольном треугольнике катет, лежащий против угла в \(30^{\circ}\) равен половине гипотенузы, тогда \(DE = 0,5\cdot CD = 3\). При этом \(ABCE\) – прямоугольник, \(AE = BC = 4\), тогда \(AD = AE + ED = 4 + 3 = 7\).
В трапеции средняя линия равна полусумме оснований. \(0,5(BC + AD) = 0,5(4 + 7) = 5,5\), значит, длина средней линии равна \(5,5\).
В трапеции \(ABCD\) средняя линия составляет \(\dfrac{4}{5}\) одного из оснований. Найдите отношение длины другого основания к длине средней линии.

Средняя линия трапеции равна полусумме оснований. Полусумма оснований трапеции \(ABCD\) составляет \(0,8\) одного из оснований, тогда сумма оснований трапеции \(ABCD\) составляет \(2\cdot 0,8 = 1,6\) этого основания, обозначим его за \(AD\). Тогда \(BC + AD = 1,6AD\), откуда \(BC = 0,6AD\). Средняя линия равна \(0,8AD\), тогда отношение длины основания \(BC\) к длине средней линии равно \(0,6 : 0,8 = 0,75\).
\(ABCD\) – трапеция с основаниями \(AD\) и \(BC\). При этом \(AB = CD = 6\), \(BC = 4\), один из углов трапеции \(ABCD\) равен \(60^{\circ}\). Найдите \(AD\).

Пусть \(\angle A = 60^{\circ}\), \(BE\) – высота в треугольнике \(ABD\). \(\angle ABE = 90^{\circ} - 60^{\circ} = 30^{\circ}\). Катет, лежащий против угла в \(30^{\circ}\), равен половине гипотенузы, тогда \(AE = 0,5\cdot 6 = 3\).
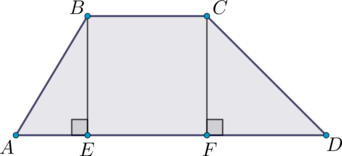
У равнобедренной трапеции углы при одном основании равны, тогда \(\angle D = 60^{\circ}\). Пусть \(CF\) – высота в треугольнике \(ACD\), тогда аналогично тому, как находили \(AE\), находим, что \(FD = 3\). \(EF
= BC\), так как \(BCFE\) – прямоугольник. Тогда \(AD = AE + EF + FD = 3
+ 4 + 3 = 10\).
В трапеции \(ABCD\): \(AB = CD\), \(\angle C - \angle A = 80^{\circ}\). Найдите \(\angle D + \angle B - \angle C\). Ответ дайте в градусах.

У равнобедренной трапеции углы при одном основании равны, тогда \(\angle B = \angle C\) и, следовательно, \(\angle D + \angle B - \angle C = \angle D = \angle A\).
У равнобедренной трапеции сумма противоположных углов равна \(180^{\circ}\) (так как \(\angle C = \angle B\), а \(\angle A + \angle B = 180^{\circ}\), как сумма односторонних при параллельных прямых и секущей).
\(\angle A + \angle C = 180^{\circ}\),
\(\angle C - \angle A = 80^{\circ}\)
тогда, вычитая из верхнего равенства нижнее, получаем \(2\cdot \angle
A = 100^{\circ}\). В итоге имеем: \(\angle D + \angle B - \angle C =
\angle A = 50^{\circ}\).


