Площадь треугольника (страница 4)
Готовиться с нами - ЛЕГКО!

Найдите площадь треугольника со сторонами \(22\), \(\sqrt{197}\) и \(\sqrt{65}\).
Рассмотрим этот треугольник. Проведем высоту к стороне, равной \(22\):

Обозначим эту высоту за \(h\), а отрезки, на которые она разбила сторону, за \(x\) и \(22-x\). Запишем теорему Пифагора для двух получившихся прямоугольных треугольников:
\(\begin{cases} 197=h^2+(22-x)^2\\ 65=h^2+x^2 \end{cases} \quad \Leftrightarrow \quad \begin{cases} 197-65=(22-x)^2-x^2\\ 65=h^2+x^2 \end{cases} \quad \Leftrightarrow \)
\(\Leftrightarrow \quad \begin{cases} 132=(22-x-x)(22-x+x)\\ 65=h^2+x^2 \end{cases} \quad \Leftrightarrow \quad \begin{cases} x=8\\ h=1 \end{cases}\)
Таким образом, площадь этого треугольника равна
\[S=\dfrac12\cdot 1\cdot 22=11\]
Найдите площадь треугольника со сторонами \(6\), \(5\) и \(\sqrt{13}\).
Применим формулу Герона для поиска площади треугольника:
\(S=\sqrt{\dfrac{6+5+\sqrt{13}}2\cdot \left(\dfrac{6+5+\sqrt{13}}2-\sqrt{13}\right)\cdot \left(\dfrac{6+5+\sqrt{13}}2-5\right)\cdot \left(\dfrac{6+5+\sqrt{13}}2-6\right)}=\)
\(=\sqrt{\dfrac{6+5+\sqrt{13}}2\cdot \dfrac{6+5-\sqrt{13}}2\cdot \dfrac{6+\sqrt{13}-5}2\cdot \dfrac{5+\sqrt{13}-6}2}=\)
\(=\sqrt{\dfrac{11+\sqrt{13}}2\cdot \dfrac{11-\sqrt{13}}2\cdot \dfrac{\sqrt{13}+1}2\cdot \dfrac{\sqrt{13}-1}2}=\dfrac14\cdot \sqrt{\left(11^2-(\sqrt{13})^2\right)\cdot \left((\sqrt{13})^2-1^2\right)}=\)
\(=\dfrac14\cdot \sqrt{(121-13)(13-1)}=\dfrac14\cdot \sqrt{(4\cdot 3\cdot 9)\cdot (4\cdot 3)}=\dfrac14\cdot 2\cdot 3\cdot 3\cdot 2=9\).
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(150^\circ\). Найдите боковую сторону этого треугольника, если его площадь равна \(100\).

Пусть \(a\) – боковая сторона треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[\dfrac12\cdot a^2\cdot \sin30^\circ=S=100\quad\Rightarrow\quad
a^2=400\quad\Rightarrow\quad a=20\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(30^\circ\). Найдите боковую сторону этого треугольника, если его площадь равна \(25\).

Пусть \(a\) – боковая сторона треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[\dfrac12\cdot a^2\cdot \sin30^\circ=S=25\quad\Rightarrow\quad
a^2=100\quad\Rightarrow\quad a=10\]
Найдите площадь треугольника, две стороны которого равны \(8\) и \(12\), а угол между ними равен \(30^\circ\).
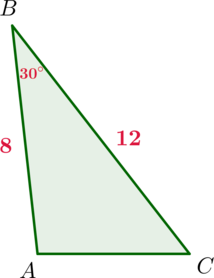
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 8\cdot 12 \cdot \dfrac12=24\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(150^\circ\). Боковая сторона треугольника равна \(20\). Найдите площадь этого треугольника.

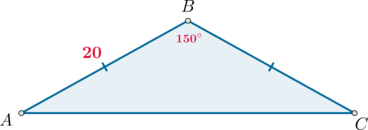
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 20^2 \cdot \dfrac12=100\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(30^\circ\). Боковая сторона треугольника равна \(10\). Найдите площадь этого треугольника.

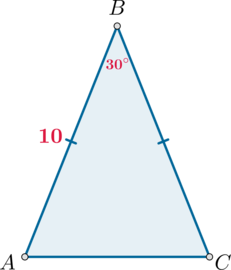
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 10^2 \cdot \dfrac12=25\]



