Площадь треугольника (страница 5)
Готовиться с нами - ЛЕГКО!

Найдите высоту треугольника, проведенную к стороне длиной \(8\), если высота, проведенная к стороне длиной \(6\), равна \(4\).
Т.к. площадь треугольника равна полупроизведению высоты и стороны, к которой эта высота проведена, то с одной стороны площадь равна \[S=\dfrac12\cdot 6\cdot 4,\]
а с другой \[S=\dfrac12\cdot 8\cdot h,\]
где \(h\) – высота, которую нужно найти. Таким образом, получаем следующее равенство:
\[\dfrac12\cdot 6\cdot 4=\dfrac12\cdot 8\cdot h \quad \Leftrightarrow \quad h=3.\]
В прямоугольном треугольнике гипотенуза равна \(\sqrt[4]3\), а один из углов равен \(30^\circ\). Найдите площадь этого треугольника.
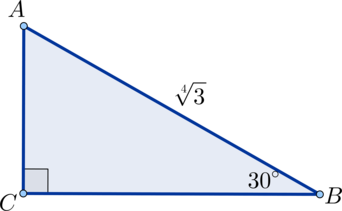
Т.к. катет, лежащий против угла в \(30^\circ\), равен половине гипотенузы, то \(AC=0,5\cdot AB=0,5\cdot \sqrt[4]3\).
Т.к. \(\angle A=90^\circ -\angle B=60^\circ\), то площадь равна \[S=\dfrac12\cdot AC\cdot AB\cdot \sin 60^\circ=\dfrac12\cdot 0,5\cdot \sqrt[4]3\cdot \sqrt[4]3\cdot \dfrac{\sqrt3}2=\dfrac38=0,375.\]
Катеты прямоугольного треугольника относятся как \(5:4\), а площадь равна \(4,1\). Найдите гипотенузу этого треугольника.
Т.к. катеты относятся как \(5:4\), то их можно обозначить за \(4x\) и \(5x\). Тогда необходимо найти гипотенузу, по теореме Пифагора равную \(\sqrt{25x^2+16x^2}=\sqrt{41x^2}\).
Т.к. площадь прямоугольного треугольника равна полупроизведению катетов, то \(S=0,5\cdot 5x\cdot 4x=10x^2=4,1\). Следовательно, \(x^2=0,41\).
Значит, гипотенуза равна \[\sqrt{41\cdot 0,41}=\sqrt{41\cdot 41\cdot 0,01}=41\cdot 0,1=4,1.\]
Дан треугольник \(ABC\). На сторонах \(AB\) и \(BC\) отмечены точки \(A'\) и \(C'\) соответственно. Известно, что \(BC'=0,5BC=4\), \(AB=14\), \(S_{ABC}=7S_{A'BC'}\). Найдите \(A'B\).
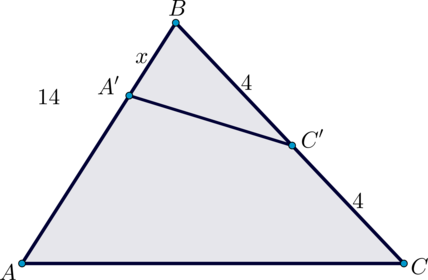
Площадь треугольника \(ABC\) равна \(S_{ABC}=0,5\cdot 14 \cdot 8\cdot \sin\angle B\).
Площадь треугольника \(A'BC'\) равна \(S_{A'BC'}=0,5\cdot A'B\cdot 4\cdot \sin\angle B\).
Таким образом, имеем равенство:
\[0,5\cdot 14 \cdot 8\cdot \sin\angle B=7\cdot 0,5\cdot A'B\cdot 4\cdot \sin\angle B \quad \Leftrightarrow \quad A'B=4.\]
В треугольнике \(ABC\): \(\angle C = 90^{\circ}\), \(CM\) – медиана, \(AC = 4\), \(CM = 2,5\). Найдите периметр треугольника \(ABC\).
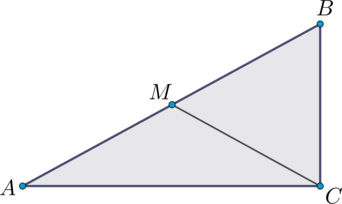
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда \(AB = 2,5 \cdot 2 = 5\). По теореме Пифагора: \(AB^2 = AC^2 + CB^2\), откуда находим \(CB = 3\). Периметр треугольника \(ABC\) равен \(3 + 4 + 5 = 12\).
Точка \(D\) лежит на стороне \(AC\) треугольника \(ABC\). Периметр треугольника \(ABD\) равен \(10\), периметр треугольника \(BDC\) равен \(7\), \(BD = 3\). Найдите периметр треугольника \(ABC\).
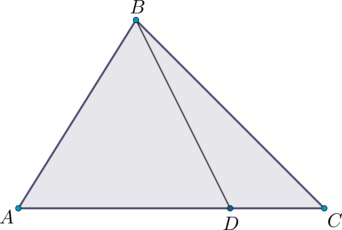
Периметр треугольника \(ABC\) равен \(AB + AC + BC\).
Периметр треугольника \(BDC\) равен \(BD + DC + BC = 7\), а \(BD = 3\), тогда \(DC + BC = 4\),
периметр треугольника \(ABD\) равен \(AB + BD + AD = 10\), тогда \(AB + AD = 7\).
\(AB + AC + BC = AB + AD + DC + BC = 4 + 7 = 11\).
В треугольнике \(ABC\): \(BD\) – высота, \(AD = 1\), \(DC = 3\), \(\angle DBC = 45^{\circ}\). Найдите площадь треугольника \(ABC\).
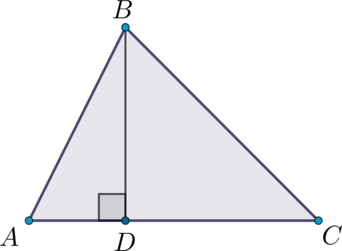
\(\angle BCD = 90^{\circ} - \angle DBC = 45^{\circ} = \angle DBC\), тогда \(BD = DC = 3\). Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию, тогда площадь треугольника \(ABC\) равна \(0,5 \cdot (3 + 1) \cdot 3 = 6\).



