Теорема Пифагора (страница 2)
Готовиться с нами - ЛЕГКО!

От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли. Расстояние от дома до столба 8 м. Вычислите длину провода. Ответ дайте в метрах.
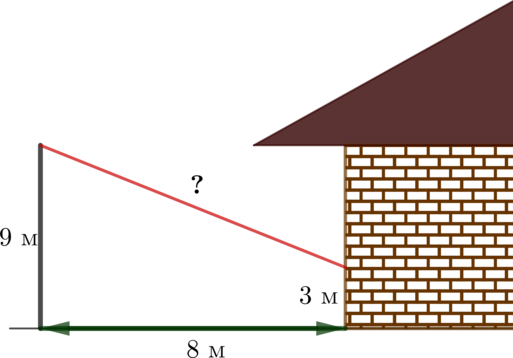
Проведем прямую \(BC\) параллельно земле, как показано на рисунке.
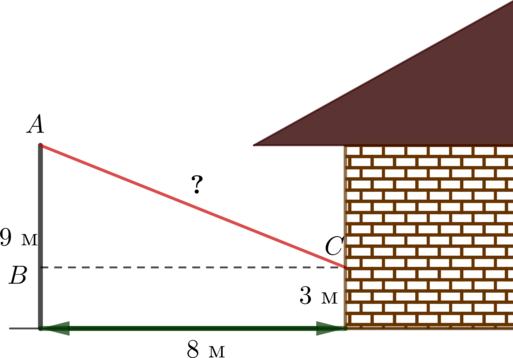
Тогда мы получим прямоугольный треугольник \(ABC\), причем \(BC=8\), \(AB=9-3=6\). Тогда длина провода \(AC=\sqrt{8^2+6^2}=10\) (м).
Лестница соединяет точки \(A\) и \(B\). Высота каждой ступени равна 12,5 см, а длина – 30 см. Расстояние между точками \(A\) и \(B\) составляет 6,5 м. Найдите высоту, на которую поднимается лестница (в метрах).

Во-первых, переведем высоту и длину ступенек в метры: \(0,125\) м и \(0,3\) м.
Во-вторых, если \(x\) – число ступенек, то \(0,125x\) – длина \(BC\), а \(0,3x\) – длина \(AC\). Треугольник \(ABC\) прямоугольный, следовательно, \[AB^2=AC^2+BC^2\quad\Rightarrow\quad 6,5^2=(0,125x)^2+(0,3x)^2\] Заметим, что \(0,125=\frac18\), \(0,3=\frac3{10}\) и \(6,5=\frac{13}2\). Тогда \[x^2=\dfrac{169\cdot 64\cdot 100}{4\cdot (100+9\cdot
64)}=400\quad\Rightarrow\quad x=20.\] Тогда \(BC=0,125\cdot 20=2,5\) (м).
Мальчик прошел от дома на восток 80 м. Потом он повернул на север и прошел еще 60 м. На каком расстоянии (в метрах) от дома оказался мальчик в итоге?
Угол между направлением “на север”\(\,\) и направлением “на восток”\(\,\) равен \(90^{\circ}\). Воспользуемся теоремой Пифагора.
Расстояние, которое мальчик прошел — катеты прямоугольного треугольника. Расстояние, которое нужно найти — гипотенуза.
\[80^2 + 60^2 = 10000\]
Значит, он находится на расстоянии 100 метров от дома.
Девочка прошла от дома на юг 50 м. Потом она повернула на восток и прошла еще какое-то расстояние. Какое расстояние прошла девочка на восток (в метрах), если она оказалась на расстоянии 130 м от дома?
Угол между направлением “на юг”\(\,\) и направлением “на восток”\(\,\) равен \(90^{\circ}\). Воспользуемся теоремой Пифагора.

Расстояние, которое девочка прошла на юг — катет прямоугольного треугольника. Расстояние, на котором она оказалась, — гипотенуза. Расстояние, которое нужно найти — другой катет.
\[130^2 - 50^2 = 14400\]
Значит, на восток девочка прошла 120 метров.
В 32 метрах одна от другой растут 2 сосны. Высота одной из них 37 м, а второй — 13 м. Каково расстояние (в метрах) между их верхушками?
Обозначим \(AF\) — высоту большей сосны, \(BD\) — меньшей.
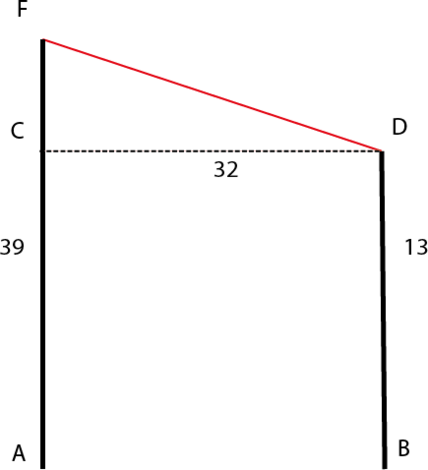
Расстояние между ними — перпендикуляр \(CD=32\). Отрезок \(CF = 37-13=24\) м. Тогда по теореме Пифагора:
\[FD^2=24^2 + 32^2.\]
Откуда \(FD = 40\) метров.
Площадь прямоугольного земельного участка равна 11 га. Ширина участка равна 200 метров. Найдите длину этого участка.
Переведем площадь участка из гектаров в квадратные метры 11 га = 110000 \(\text{м}^2\).
Площадь прямоугольника равна произведению его сторон. Значит, длина равна \(110000:200 = 550\) метров.
Площадь прямоугольного земельного участка равна 17 га. Ширина участка равна 400 метров. Найдите длину этого участка.
Переведем площадь участка из гектаров в квадратные метры 11 га = 170000 \(\text{м}^2\).
Площадь прямоугольника равна произведению его сторон. Значит, длина равна \(170000:400 = 425\) метров.



