Нахождение приближенного значения корня (страница 2)
Готовиться с нами - ЛЕГКО!

Какое из чисел отмечено на координатной прямой точкой \(A\)?
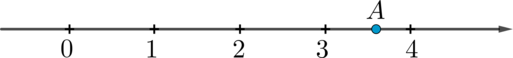
1) \(\sqrt{7}\qquad \) 2) \(\sqrt{11}\qquad \) 3) \(\sqrt{13}\qquad \) 4) \(\sqrt{15}\)
Точка \(A\) находится между числами \(3=\sqrt 9\) и \(4=\sqrt{16}\). В этом же промежутке находятся три числа из пунктов 2, 3 и 4.
Заметим, что точка \(A\) находится чуть правее середины отрезка \([3;4]\). Так как \(\sqrt{11}<3,5\) (так как \(3,5=\sqrt{12,25}\)), то это число отпадает.
Так как точка \(A\) находится очень близко к середине, то выбираем число \(\sqrt{13}\). Ответ 3.
Одна из точек, отмеченных на координатной прямой, соответствует числу \(\sqrt{23}\). Какая это точка?

1) \(M\qquad \) 2) \(N\qquad \) 3) \(P\qquad \) 4) \(Q\)
Число \(\sqrt{23}\) лежит между числами \(\sqrt{16}=4\) и \(\sqrt{25}=5\), причем ближе к \(5\) (то есть правее \(4,5\)). Следовательно, это точка \(P\). Ответ 3.
Одно из чисел \(\sqrt{105}, \sqrt{116}, \sqrt{128}, \sqrt{140}\) отмечено на координатной прямой. 
Какое это число?
1) \(\sqrt{105}\) \(\;\;\;\) 2)\(\sqrt{116}\) \(\;\;\;\) 3)\(\sqrt{128}\) \(\;\;\;\) 4)\(\sqrt{140}\)
Точка лежит между числами \(11 = \sqrt{121}\) и \(12 = \sqrt{144}\). В этом промежутке находятся точки \(\sqrt{128}\) и \(\sqrt{140}\). При этом \(\sqrt{128} < \sqrt{132,5}\) (середины отрезка [11;12]), а \(\sqrt{140} > \sqrt{132,5}\). Значит, искомая точка — \(\sqrt{128}\).
Одно из чисел \(\sqrt{27}, \sqrt{32}, \sqrt{38}, \sqrt{45}\) отмечено на координатной прямой. 
Какое это число?
1) \(\sqrt{27}\) \(\;\;\;\) 2)\(\sqrt{32}\) \(\;\;\;\) 3)\(\sqrt{38}\) \(\;\;\;\) 4)\(\sqrt{45}\)
Точка лежит между числами \(5 = \sqrt{25}\) и \(6 = \sqrt{36}\). В этом промежутке находятся точки \(\sqrt{27}\) и \(\sqrt{32}\). При этом \(\sqrt{27} < \sqrt{30,5}\) (середины отрезка [5;6]), а \(\sqrt{32} > \sqrt{30,5}\). Значит, искомая точка — \(\sqrt{27}\).
На координатной прямой отмечены точка A, B, C и D. 
Какой точке соответствует число \(\sqrt{79}\)?
1) Точке A \(\;\;\;\) 2)Точке B \(\;\;\;\) 3)Точке С \(\;\;\;\) 4)Точке D
Число \(\sqrt{79}\) лежит на отрезке \([8 = \sqrt{64}; 9 = \sqrt{81}]\) правее его середины (\(\sqrt{79} > \sqrt{72,5}\)). Значит, числу \(\sqrt{79}\) соответствует точка D.
На координатной прямой отмечены точка A, B, C и D. 
Какой точке соответствует число \(\sqrt{69}\)?
1) Точке A \(\;\;\;\) 2)Точке B \(\;\;\;\) 3)Точке С \(\;\;\;\) 4)Точке D
Число \(\sqrt{69}\) лежит на отрезке \([8 = \sqrt{64}; 9 = \sqrt{81}]\) левее его середины (\(\sqrt{69} < \sqrt{72,5}\)). Значит, числу \(\sqrt{69}\) соответствует точка C.
Какое из чисел принадлежит промежутку \([10;11]\)?
1) \(\sqrt{111}\) \(\;\;\;\) 2)\(\sqrt{125}\) \(\;\;\;\) 3)\(\sqrt{136}\) \(\;\;\;\) 4)\(\sqrt{140}\)
В промежуток \([10 = \sqrt{100};11 = \sqrt{121}]\) попадает только число \(\sqrt{111}\).



