Задачи по теме «Пирамида» (страница 2)
Готовиться с нами - ЛЕГКО!

Пирамида \(PA_1A_2...A_n\):
\(\blacktriangleright\) Многоугольник \(A_1...A_n\) – основание;
треугольники \(PA_1A_2, PA_2A_3\) и т.д. – боковые грани;
точка \(P\) – вершина;
отрезки \(PA_1, PA_2, ..., A_1A_2\) и т.д. – ребра.
\(\blacktriangleright\) Если в основании пирамиды лежит треугольник, то она называется тетраэдром.
\(\blacktriangleright\) Высота пирамиды – перпендикуляр, опущенный из вершины \(P\) к основанию.
\(\blacktriangleright\) Объем пирамиды \({\Large{V=\dfrac{1}{3}S_{\text{осн}}h}}\) , где \(S_{\text{осн}}\) – площадь основания, \(h\) – высота.
\(\blacktriangleright\) Площадь боковой поверхности – сумма площадей всех боковых граней.
Площадь полной поверхности – сумма площади боковой поверхности и площади основания.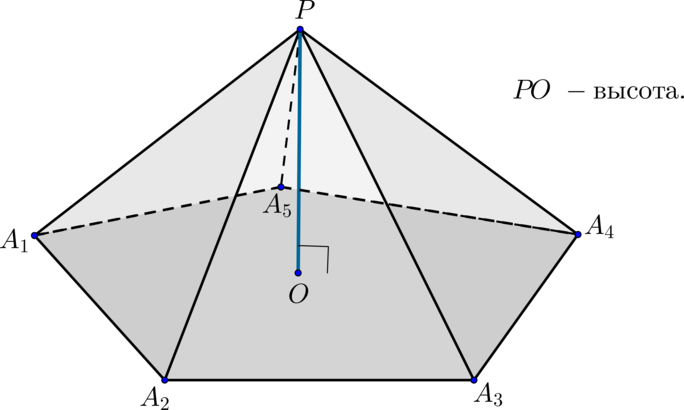
Заметим, что принято записывать название пирамиды, начиная с вершины.
\(EABCD\) – пирамида, \(ABCD\) – параллелограмм со сторонами \(1\) и \(\sqrt{3}\), \(\angle BAD = 60^{\circ}\). Из точки \(E\) опущен перпендикуляр \(EN\) на плоскость \((ABCD)\), причём точка \(N\) – точка пересечения диагоналей \(ABCD\), \(AE = \sqrt{5 + 0,25\sqrt{3}}\). Найдите объем пирамиды.
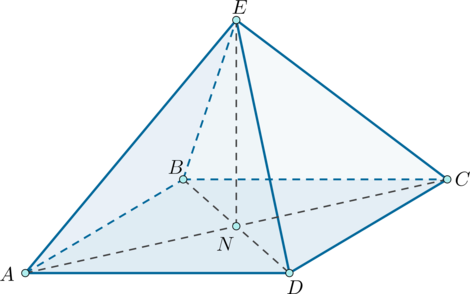
Объем пирамиды может быть найден по формуле \(V = \dfrac{1}{3}S\cdot h\), где \(S\) – площадь основания пирамиды, \(h\) – высота пирамиды.
Площадь параллелограмма может быть найдена по формуле \(S_\text{пар.} = ab\cdot\sin\alpha\), где \(a\), \(b\) – не параллельные стороны параллелограмма, \(\alpha\) – угол между ними. \[S_{ABCD} = 1\cdot\sqrt{3}\cdot\sin 60^{\circ} = \sqrt{3}\cdot\dfrac{\sqrt{3}}{2} = \dfrac{3}{2}.\]
Найдем \(EN\):
по теореме Пифагора для треугольника \(AEN\): \[EN^2 = AE^2 - AN^2.\]
Так как диагонали параллелограмма точкой пересечения делятся пополам, то \(AN = \dfrac{1}{2}AC\).
Найдем \(AC\) по теореме косинусов для треугольника \(ACD\): \[AC^2 = AD^2 + DC^2 - 2\cdot AD\cdot DC\cdot\cos\angle ADC,\] но \(\angle ADC = 180^{\circ} - \angle BAD = 120^{\circ}\), тогда \[AC^2 = 1 + 3 - 2\cdot 1\cdot\sqrt{3}\cdot\left(-\dfrac{1}{2}\right) = 4 + \sqrt{3},\] откуда \[AN = \dfrac{1}{2}AC = \dfrac{1}{2}\sqrt{4 + \sqrt{3}}.\] Теперь \(EN^2 = 5 + \dfrac{\sqrt{3}}{4} - 1 - \dfrac{\sqrt{3}}{4} = 4\), тогда \(EN = 2\), следовательно,
\[V_\text{пирамиды} = \dfrac{1}{3}\cdot \dfrac{3}{2}\cdot 2 = 1.\]
\(EABCD\) – пирамида, \(ABCD\) – прямоугольник со сторонами \(3 + 3\sqrt{5}\) и \(\sqrt{114} + \sqrt{570}\). Из точки \(E\) опущен перпендикуляр \(EM = \sqrt{55}\) на плоскость \((ABCD)\), причём точка \(M\) попала на \(AC\) так, что \(AM : MC = 1 : \sqrt{5}\). Пусть \(S\) – площадь поверхности пирамиды \(ABCDE\). Найдите \(\dfrac{S}{1 + \sqrt{5}} - \sqrt{114}(12 + 3\sqrt{5})\).
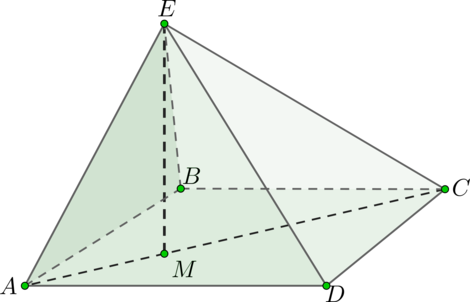
Пусть \(AD = 3 + 3\sqrt{5}\). Рассмотрим прямоугольник \(ABCD\)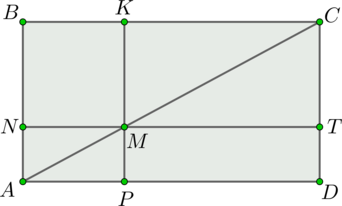
Достроим отрезки \(NT\) и \(PK\), проходящие через точку \(M\), как показано на рисунке (\(NT \parallel BC\), \(PK \parallel AB\)).
Тогда \(MN = 3\), \(MT = 3\sqrt{5}\), \(MP = \sqrt{114}\), \(MK = \sqrt{570}\). \(MN\) – проекция \(NE\) на \((ABCD)\), \(MN\) перпендикулярен \(AB\), тогда по теореме о трех перпендикулярах \(NE\) перпендикулярен \(AB\). По теореме Пифагора \(NE = 8\). Площадь треугольника \(ABE\) равна \[\dfrac{1}{2}\cdot AB\cdot NE = 4\cdot\sqrt{114}\cdot(1 + \sqrt{5}).\] Аналогично площадь треугольника \(BEC\) равна \(37,5(1 + \sqrt{5})\),
площадь треугольника \(CDE\) равна \(5\cdot\sqrt{114}\cdot(1 + \sqrt{5})\),
площадь треугольника \(AED\) равна \(19,5(1 + \sqrt{5})\),
площадь прямоугольника \(ABCD\) равна \(3\sqrt{114}(1 + \sqrt{5})^2\).
Площадь поверхности пирамиды: \[S = 9\cdot\sqrt{114}\cdot(1 + \sqrt{5}) + 57(1 + \sqrt{5}) + 3\sqrt{114}(1 + \sqrt{5})^2.\] Тогда \(\dfrac{S}{1 + \sqrt{5}} - \sqrt{114}(12 + 3\sqrt{5}) = 57\).
\(EABCD\) – пирамида, \(\angle ABC = \angle BCD = \angle CDA = 90^{\circ}\), \(AD = DC = a\), проекция точки \(E\) на плоскость \(ABC\) – середина \(AC\). Длина отрезка, соединяющего точку \(E\) и середину \(BD\), равна \(0,5a\sqrt{3}\), площадь полной поверхности пирамиды равна \(2,4\). Найдите \(DE\).
Так как \(\angle ABC = \angle BCD = \angle CDA = 90^{\circ}\), то \(\angle DAB = 360^{\circ} - 3\cdot 90^{\circ} = 90^{\circ}\), тогда \(ABCD\) – прямоугольник, но \(AD = DC\), следовательно, \(ABCD\) – квадрат.
Обозначим отрезок, соединяющий точку \(E\) и середину \(BD\) через \(h\).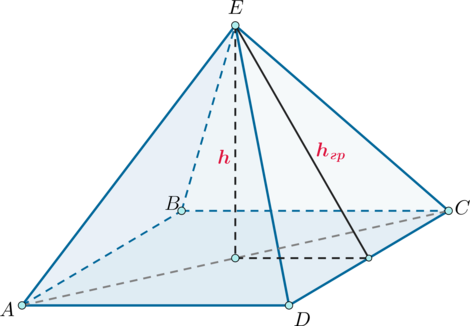
Так как \(ABCD\) – квадрат, то \(h\) соединяет точку \(E\) с серединой \(AC\), то есть проекцией точки \(E\) на \((ABC)\), откуда заключаем, что \(h\) перпендикулярен \((ABC)\). Через \(h_\text{гр}\) обозначим перпендикуляр, опущенный из точки \(E\) на \(DC\).
Пирамида \(ABCDE\) является правильной по определению. Тогда её грани равные равнобедренные треугольники и площадь её полной поверхности равна \(a^2 + 4\cdot S_{EDC} = a^2 + 2\cdot a\cdot h_\text{гр}\).
По теореме Пифагора \[h_\text{гр} = \sqrt{h^2 + \dfrac{a^2}{4}} = \sqrt{\dfrac{3a^2}{4} + \dfrac{a^2}{4}} = a,\] тогда \(S_{ABCDE} = a^2 + 2a^2 = 3a^2 = 2,4\), откуда \(a^2 = 0,8\).
По теореме Пифагора \[ED^2 = {h_\text{гр}}^2 + \dfrac{a^2}{4} = a^2 + \dfrac{a^2}{4} = \dfrac{5}{4}\cdot a^2 = \dfrac{5}{4}\cdot 0,8 = 1,\] откуда \(ED = 1\).


