Ромб и его свойства
Готовиться с нами - ЛЕГКО!

Сумма внутренних углов любого четырехугольника равна \(360^\circ\).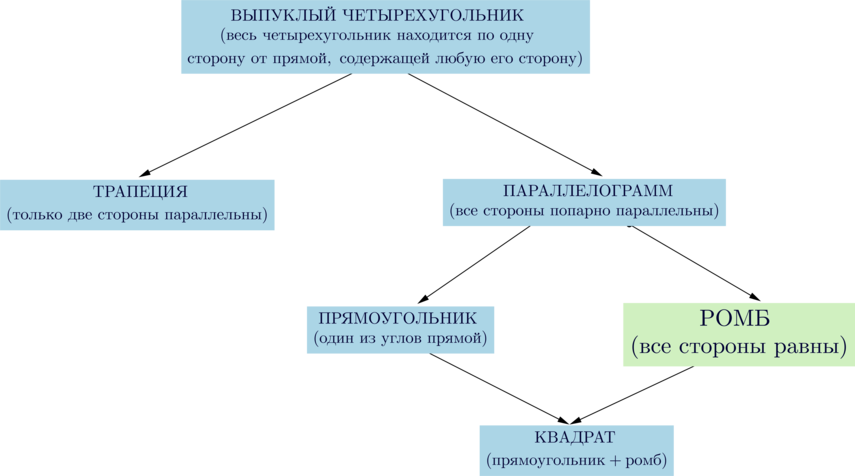
Свойства ромба:
\(\blacktriangleright\) Те же, что и у параллелограмма:
\(\sim\) Противоположные стороны попарно равны;
\(\sim\) Диагонали точкой пересечения делятся пополам;
\(\sim\) Противоположные углы попарно равны, а сумма соседних равна \(180^\circ\);
\(\blacktriangleright\) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.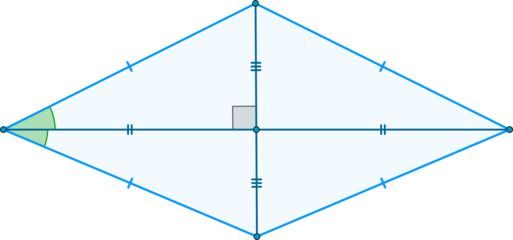
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
\(\blacktriangleright\) все стороны равны;
\(\blacktriangleright\) диагонали взаимно перпендикулярны и он является параллелограммом;
\(\blacktriangleright\) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.
2. Площадь ромба равна половине произведения его диагоналей.
В ромбе \(ABCD\): \(\angle ACD = 26^{\circ}\). Найдите \(\angle ABD\). Ответ дайте в градусах.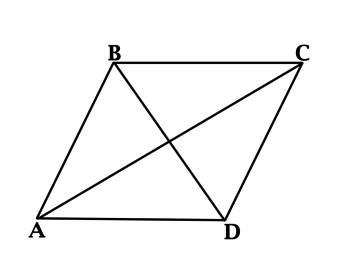
В ромбе диагонали перпендикулярны, тогда \(\angle CDB = 90^{\circ} - \angle ACD = 64^{\circ}\).
\(BC = CD\), тогда \(\angle CBD = \angle CDB = 64^{\circ}\).
Так как диагонали ромба делят его углы пополам, то \(\angle ABD = \angle CBD = 64^{\circ}\).
Найдите большую диагональ ромба \(ABCD\), если \(AB = 2\sqrt{3}\), а острый угол равен половине тупого.
Так как сумма односторонних углов при параллельных прямых и секущей равна \(180^{\circ}\), то сумма острого и тупого углов ромба равна \(180^{\circ}\).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба \(ABCD\) равен \(60^{\circ}\).
Треугольник \(ABD\) – равнобедренный, один из углов которого равен \(60^{\circ}\), тогда треугольник \(ABD\) – равносторонний и \(BD = 2\sqrt{3}\).
Пусть \(O\) – точка пересечения диагоналей ромба, тогда \(OD = 0,5 BD = \sqrt{3}\), следовательно, по теореме Пифагора находим: \(AO^2 + OD^2 = AD^2\), тогда \(AO^2 + 3 = 12\), откуда находим \(AO = 3\). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, \(AC = 6\).
Острый угол ромба \(ABCD\) равен \(60^{\circ}\), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.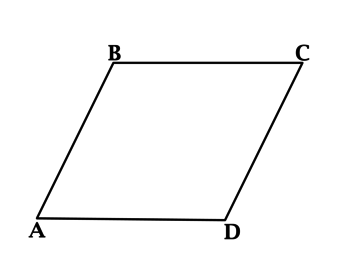
Пусть \(\angle A = 60^{\circ}\). В ромбе все стороны равны, тогда треугольник \(ABD\) – равнобедренный, у которого один из углов равен \(60^{\circ}\), следовательно, треугольник \(ABD\) – равносторонний и \(BD = 10\).
Треугольник \(ABC\) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда \(AC > AB = BD\), значит, \(BD\) – меньшая из диагоналей.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно \(3\), а острый угол ромба равен \(60^\circ\). Найдите большую диагональ ромба.

Пусть в ромбе \(ABCD\): \(O\) – точка пересечения диагоналей, \(OH\) – расстояние до стороны \(AB\), \(\angle DAB = 60^\circ\), тогда \(\angle OAB = 30^\circ\). Получаем, что \(OH\) – катет лежащий напротив угла в \(30^\circ\), значит \(AO = 2\cdot OH = 6\). Т.к. \(AC\) и есть большая диагональ, то \(AC = 2\cdot AO = 12\).
Сторона ромба равна \(4\). Расстояние от точки пересечения его диагоналей до одной из сторон равно \(1\). Найдите площадь ромба.
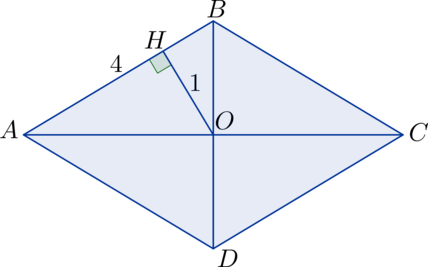
Пусть в ромбе \(ABCD\): \(O\) – точка пересечения диагоналей, \(OH\) – расстояние до стороны \(AB\), тогда \(S_{\triangle ABO} = \frac{1}{2}\cdot 1 \cdot 4 = 2\). Диагонали ромба делят его на \(4\) равных прямоугольных треугольника \(\Rightarrow\) \(S_{ABCD} = 4\cdot 2 = 8\).
Периметр ромба равен \(40\), а диагонали относятся, как \(3:4\). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении \(3:4\). Зная периметр, найдем сторону ромба: \(40
: 4 = 10\). Сторона и половинки диагоналей образуют прямоугольный треугольник \(AOB\).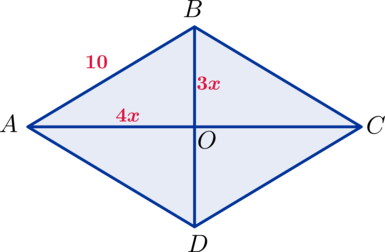
Пусть \(AO=4x\), \(BO=3x\).
Тогда по теореме Пифагора: \((3x)^2 + (4x)^2 = 10^2\) \(\Rightarrow\) \(25x^2 = 100\) \(\Rightarrow\) \(x^2 = 4\) \(\Rightarrow\) \(x = 2\). Диагонали равны \(BD=2BO=12\) и \(AC=2AO=16\) \(\Rightarrow\) \(S_{ABCD} =
\frac{1}{2}\cdot12\cdot16 = 96\).

Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как \(3:1\)?
Пусть \(\angle B\) и \(\angle B_1\) – равные углы ромбов. Так как стороны ромбов относятся как \(3:1\), то можно обозначить их за \(3x\) и \(x\) соответственно.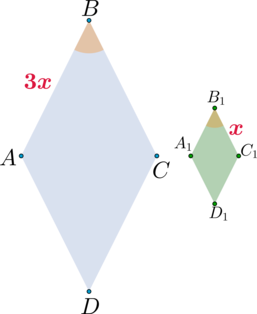
Тогда и \(\angle D=\angle D_1\) (так как у ромба противоположные углы равны). Следовательно, \(\triangle ABC\sim \triangle A_1B_1C_1\) и \(\triangle ADC\sim\triangle A_1D_1C_1\) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен \(3\). Следовательно, их площади относятся как \(9:1\). А так как \(S_{ABC}+S_{ADC}=S_{ABCD}\) и \(S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}\), то \(S_1:S_2=9:1\).
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.



