Ромб и его свойства (страница 2)
Готовиться с нами - ЛЕГКО!

Сумма внутренних углов любого четырехугольника равна \(360^\circ\).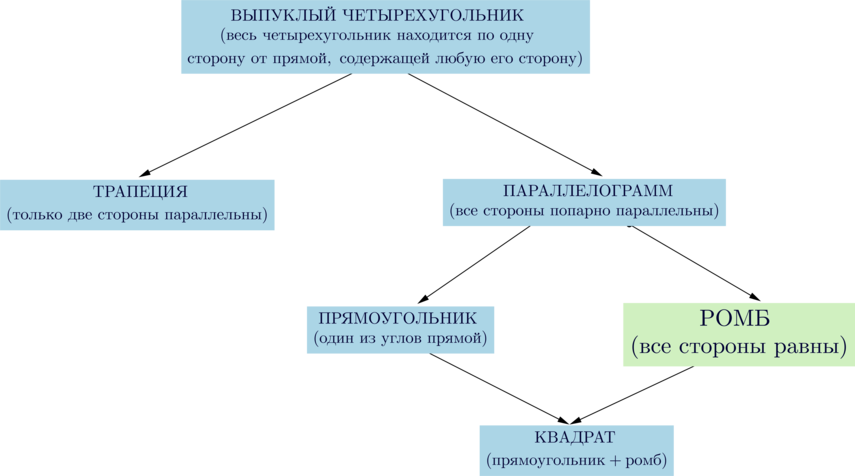
Свойства ромба:
\(\blacktriangleright\) Те же, что и у параллелограмма:
\(\sim\) Противоположные стороны попарно равны;
\(\sim\) Диагонали точкой пересечения делятся пополам;
\(\sim\) Противоположные углы попарно равны, а сумма соседних равна \(180^\circ\);
\(\blacktriangleright\) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.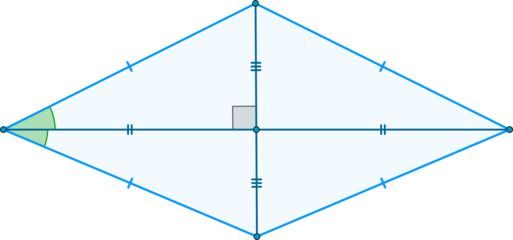
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
\(\blacktriangleright\) все стороны равны;
\(\blacktriangleright\) диагонали взаимно перпендикулярны и он является параллелограммом;
\(\blacktriangleright\) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.
2. Площадь ромба равна половине произведения его диагоналей.
Середины сторон ромба \(ABCD\) являются вершинами четырехугольника \(KLMN\). Середины сторон \(KLMN\) — четырехугольника \(PQRS\). Найдите отношение площади ромба \(ABCD\) к площади четырехугольника \(PQRS\)?
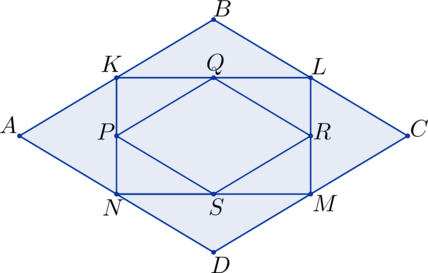
1) По теореме Вариньона \(KLMN\) – параллелограмм. Но т.к. \(KN\parallel BD, KL\parallel AC, BD\perp AC \ \Rightarrow \ KN\perp KL\), значит, \(KLMN\) — прямоугольник, причем \(S_{KLMN}=KN\cdot KL\).
Т.к. площадь ромба равна полупроизведению диагоналей, то \(S_{ABCD}=\frac12 AC\cdot BD\). Но \(KN=\frac12 BD, KL=\frac12 AC\) как средние линии, следовательно, \(S_{ABCD}=\frac12 AC\cdot BD=2KN\cdot KL=2\cdot S_{KLMN}\).
2) Аналогично \(PQRS\) – параллелограмм. Но, как средние линии, \(PQ=\frac12NL, PS=\frac12 KM\); а \(NL=KM\), значит и \(PQ=PS\). Следовательно, \(PQRS\) – ромб.
Заметим, что \(QS=KN, PR=KL\), значит, \(S_{PQRS}=\frac 12 QS\cdot PR=\frac 12 KLMN\).
Из всего этого следует, что \(S_{ABCD}=4S_{PQRS}\). Значит, отношение равно \(4\).
Найдите высоту ромба, сторона которого равна \(\sqrt3\), а острый угол равен \(60^\circ\).
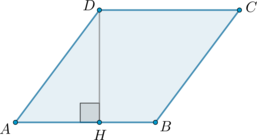
\(AD=\sqrt3\), \(\angle A=60^\circ\). Следовательно, \(\angle ADH=30^\circ\). Катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, следовательно, \(AH=0,5AD=\frac{\sqrt3}2\). Тогда по теореме Пифагора: \[DH=\sqrt{(\sqrt3)^2-\left(\dfrac{\sqrt3}2\right)^2}=\dfrac32\]
Найдите большую диагональ ромба, сторона которого равна \(\sqrt3\), а острый угол равен \(60^\circ\).

\(\angle A=60^\circ\).
Проведем диагональ \(BD\). Пусть \(AC\cap BD=O\). Докажем, что \(AC\) – большая диагональ.
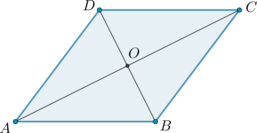
Так как в ромбе, как и в параллелограмме, диагонали точкой пересечения делятся пополам, то \(AO=0,5AC, DO=0,5BD\). Так как в ромбе диагонали являются биссектрисами углов и взаимно перпендикулярны, то \(\angle DAO=30^\circ\), \(\angle AOD=90^\circ\) и соответственно \(\angle ADO=60^\circ\). В треугольнике против большего угла лежит большая сторона, следовательно, \(AO>DO\), значит, \(AC\) – большая диагональ.
Катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, следовательно, \(DO=0,5AD=\frac{\sqrt3}2\). Тогда по теореме Пифагора: \[AO=\sqrt{(\sqrt3)^2-\left(\dfrac{\sqrt3}2\right)^2}=\dfrac32 \quad\Rightarrow\quad AC=3\]
Диагонали ромба относятся как \(4:3\). Периметр ромба равен \(200\). Найдите высоту ромба.
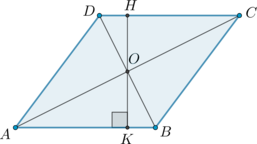
Отрезок \(HK\) – высота ромба. Так как \(AB\parallel DC\) и \(HK\perp AB\), то \(HK\perp DC\).
1 способ
Так как диагонали ромба делят его на 4 равных прямоугольных треугольника, а у равных треугольников высоты, опущенные к равным сторонам, равны, то \(OK=OH\).
Рассмотрим \(\triangle AOB\). Так как \(AC:BD=4:3\), то также \(AO:BO=4:3\). Пусть \(AO=4x, BO=3x\). Следовательно, \(AB=\sqrt{(4x)^2+(3x)^2}=5x\).
Так как у ромба все стороны равны, то его сторона равна \(200:4=50\), следовательно, \(5x=50\) и \(x=10\).
Высота прямоугольного треугольника \(AOB\), опущенная из вершины прямого угла \(O\), равна \(AO\cdot OB:AB\), следовательно, \[OK=\dfrac{4x\cdot 3x}{5x}=\dfrac{12}5x=24\quad\Rightarrow\quad HK=24\cdot 2=
48\]
2 способ
Так как у ромба все стороны равны, то его сторона равна \(AB=200:4=50\). Следовательно, площадь ромба равна \(S=50HK\) (произведение стороны на высоту, проведенную к этой стороне).
Так как \(AC:BD=4:3\), то можно принять \(AC=4a, BD=3a\). Так как площадь ромба равна полупроизведению диагоналей, то \(S=0,5\cdot
4a\cdot 3a=6a^2\), следовательно, \[50HK=6a^2\quad\Rightarrow\quad HK=\dfrac3{25}a^2\] Так как диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, то по теореме Пифагора из \(\triangle AOB\): \[\left(\dfrac32a\right)^2+(2a)^2=AB^2\quad\Rightarrow\quad a^2=400\] Следовательно, \[HK=\dfrac3{25}\cdot 400=48\]
В ромбе \(ABCD\) угол \(CDA\) равен \(78^\circ\). Найдите угол \(ACB\). Ответ дайте в градусах.
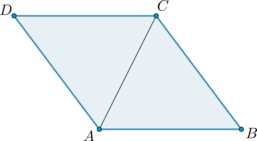
Так как в ромбе диагонали являются биссектрисами углов, то \(\angle ACB=\angle ACD\). Так как у ромба все стороны равны, то \(AD=DC\), следовательно, \(\angle CAD=\angle ACD=x\). Тогда \(x+x+\angle CDA=180^\circ\), откуда \[x=(180^\circ-78^\circ):2=51^\circ\]
В ромбе \(ABCD\) угол \(DAB\) равен \(148^\circ\). Найдите угол \(BDC\). Ответ дайте в градусах.
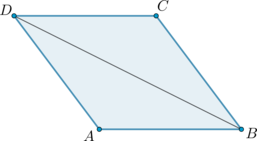
Так как в ромбе диагонали являются биссектрисами углов, то \(\angle BDC=\angle BDA\). Так как у ромба все стороны равны, то \(AD=AB\), следовательно, \(\angle BDA=\angle DBA=x\). Тогда \(x+x+\angle DAB=180^\circ\), откуда \[x=(180^\circ-148^\circ):2=16^\circ\]
Найдите площадь ромба, если его высота равна \(2\), а острый угол равен \(30^\circ\).
Проведем \(DH\perp AB\).
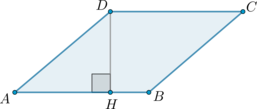
Так как \(\angle A=30^\circ\), а катет, лежащий против угла \(30^\circ\), равен половине гипотенузы, то \(AD=2DH=2\cdot 2=4\). Площадь ромба равна произведению высоты на сторону, к которой проведена высота, следовательно, \[S=DH\cdot AB=4\cdot 2=8\] (\(AB=AD\), так как в ромбе по определению все стороны равны)



