Равнобедренные и равносторонние треугольники
Готовиться с нами - ЛЕГКО!

Основные теоремы:
\(\blacktriangleright\) Вертикальные углы равны, а смежные в сумме дают \(180^\circ\): \(\alpha +\beta =180^\circ\).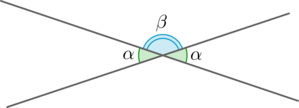
\(\blacktriangleright\) Сумма внутренних углов треугольника равна \(180^\circ\): \(\alpha+\beta+\gamma =180^\circ\)
\(\blacktriangleright\) Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: \(\phi=\alpha+\beta\)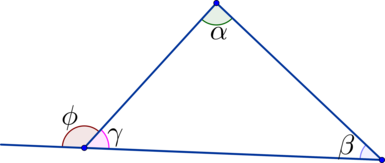
\(\blacktriangleright\) Биссектриса треугольника – отрезок, выходящий из вершины угла и делящий этот угол пополам.
\(\blacktriangleright\) Высота треугольника – отрезок, выходящий из вершины угла под углом \(90^\circ\) к противолежащей стороне (или ее продолжению).
\(\blacktriangleright\) Медиана треугольника – отрезок, выходящий из вершины угла и делящий противолежащую сторону пополам.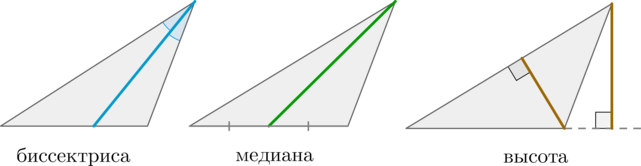
\(\blacktriangleright\) В равнобедренном треугольнике углы при основании равны.
В треугольнике \(ABC\): \(\angle B = 81^{\circ}\), \(\angle C = 25^{\circ}\). Найдите внешний угол при вершине \(A\). Ответ дайте в градусах.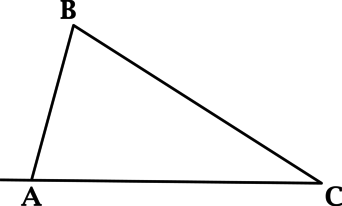
Согласно теореме о внешнем угле треугольника, \(\angle B + \angle C =\) внешнему углу при вершине \(A\), следовательно \(A_{\text{внеш}}\) \( = 81^{\circ} + 25^{\circ} = 106^{\circ}\).
В треугольнике \(ABC\): \(\angle A = 22^{\circ}\), внешний угол при вершине \(C\) равен \(130^{\circ}\). Найдите \(\angle B\). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, \(\angle A + \angle B = C_{\text{внеш}}\), тогда \(22^{\circ} + \angle B = 130^{\circ}\), откуда находим \(\angle B = 130^{\circ} - 22^{\circ} = 108^{\circ}\).
В треугольнике \(ABC\): \(\angle C = 35^{\circ}\), внешний угол при вершине \(B\) равен \(91^{\circ}\). Найдите \(\angle A\). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, \(\angle C + \angle A = B_{\text{внеш}}\), тогда \(35^{\circ} + \angle A = 91^{\circ}\), откуда находим \(\angle A = 91^{\circ} - 35^{\circ} = 56^{\circ}\).
В треугольнике \(ABC\): \(\angle C = 70^{\circ}\), \(AB = BC\). Найдите \(\angle B\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C = 70^{\circ}\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - 70^{\circ} - 70^{\circ} = 40^{\circ}\).
В треугольнике \(ABC\): \(\angle A = 47^{\circ}\), \(AB = BC\). Найдите \(\angle B\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle C = \angle A = 47^{\circ}\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - 47^{\circ} - 47^{\circ} = 86^{\circ}\).
В треугольнике \(ABC\): \(\angle C = 36^{\circ}\), \(AB = BC\). Найдите \(\angle B\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C = 36^{\circ}\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - 36^{\circ} - 36^{\circ} = 108^{\circ}\).
В треугольнике \(ABC\): \(\angle B = 38^{\circ}\), \(AB = BC\). Найдите \(\angle C\). Ответ дайте в градусах.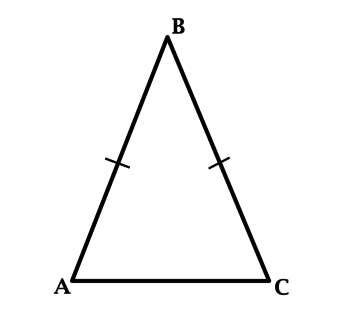
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(180^{\circ} = 38^{\circ} + \angle A + \angle C = 38^{\circ} + 2\cdot \angle A\), откуда \(2\cdot \angle A = 142^{\circ}\), тогда \(\angle A = 71^{\circ}\).
Теме «Работа с углами треугольника» в ЕГЭ по математике базового уровня традиционно посвящается несколько заданий. В зависимости от предложенных условий учащиеся могут давать как краткий, так и развернутый ответ с полным описанием алгоритма решения. Если вы хотите иметь конкурентные баллы по итогам прохождения ЕГЭ, то вам непременно стоит уделить внимание задачам на нахождение углов треугольника.
В этом вам поможет образовательный портал «Школково». Мы подготовили и изложили базовый теоретический и практический материал таким образом, чтобы все учащиеся, вне зависимости от уровня подготовки, смогли вспомнить основные понятия и без особых затруднений найти углы треугольника в задачах ЕГЭ.
Основные моменты
При решении подобных задач в ЕГЭ можно использовать теорему о сумме углов треугольника. Повторить ее вам поможет наш образовательный ресурс.
Если в условии задачи ЕГЭ не указаны величины внешних углов прямоугольного треугольника, рекомендуется обозначить их переменными. Затем используются известные свойства.
Если решение задачи на нахождение углов равнобедренного или другого треугольника в ЕГЭ не получается выстроить сразу, то, опираясь на полученные данные, необходимо начинать вычислять величины, которые можно найти. При этом учащиеся должны уметь логически выстраивать рассуждение и создавать чертежи.
Научившись правильно выполнять упражнения на нахождение углов равносторонних и других треугольников, а также углов между биссектрисами треугольника, представленные в соответствующих разделах на образовательном портале «Школково», вы сможете закрепить материал и успешно решать подобные задания в ЕГЭ.



