Равнобедренные и равносторонние треугольники (страница 6)
Готовиться с нами - ЛЕГКО!

Основные теоремы:
\(\blacktriangleright\) Вертикальные углы равны, а смежные в сумме дают \(180^\circ\): \(\alpha +\beta =180^\circ\).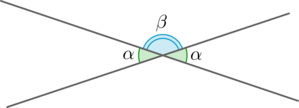
\(\blacktriangleright\) Сумма внутренних углов треугольника равна \(180^\circ\): \(\alpha+\beta+\gamma =180^\circ\)
\(\blacktriangleright\) Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: \(\phi=\alpha+\beta\)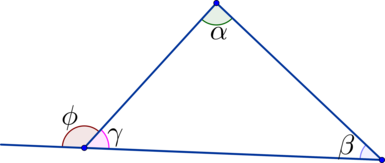
\(\blacktriangleright\) Биссектриса треугольника – отрезок, выходящий из вершины угла и делящий этот угол пополам.
\(\blacktriangleright\) Высота треугольника – отрезок, выходящий из вершины угла под углом \(90^\circ\) к противолежащей стороне (или ее продолжению).
\(\blacktriangleright\) Медиана треугольника – отрезок, выходящий из вершины угла и делящий противолежащую сторону пополам.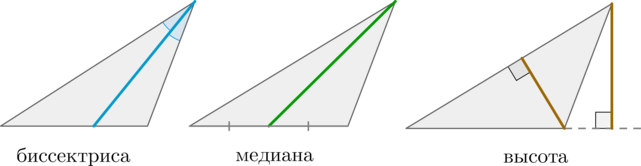
\(\blacktriangleright\) В равнобедренном треугольнике углы при основании равны.
В треугольнике \(ABC\): \(\angle A = 51^{\circ}\), \(\angle C = 77^{\circ}\), \(BD\) – биссектриса, \(P\) – такая точка на \(AB\), что \(PB = BC\). Найдите \(\angle ADP\). Ответ дайте в градусах.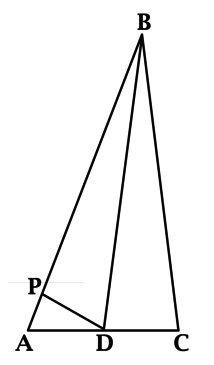
Сумма углов в треугольнике равна \(180^{\circ}\), тогда \(\angle ABC = 180^{\circ} - \angle A - \angle C = 180^{\circ} - 51^{\circ} - 77^{\circ} = 52^{\circ}\). Так как \(BD\) – биссектриса, то \(\angle CBD = 0,5\cdot \angle ABC = 26^{\circ}\).
Треугольники \(PBD\) и \(CBD\) равны по двум сторонам и углу между ними, тогда \(\angle PDB = \angle CDB\). \(\angle CDB = 180^{\circ} - \angle CBD - \angle C = 180^{\circ} - 26^{\circ} - 77^{\circ} = 77^{\circ}\), тогда \(\angle PDC = 2\cdot \angle CDB = 154^{\circ}\). Тогда \(\angle ADP = 180^{\circ} - 154^{\circ} = 26^{\circ}\).
В равнобедренном треугольнике один из углов равен \(100^\circ\). Найдите наибольший из внешних углов этого треугольника. Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, а сумма углов треугольника равна \(180^\circ\), следовательно, в треугольнике не может быть двух углов по \(100^\circ\), тогда угол при вершине равен \(100^\circ\), а углы при основании равны по \((180^\circ - 100^\circ) : 2 = 40^\circ\).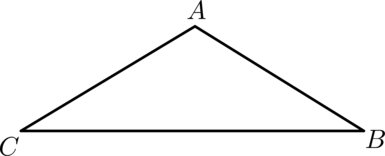
Внешние углы этого треугольника равны \[180^\circ - 100^\circ = 80^\circ,\qquad 180^\circ - 40^\circ = 140^\circ,\qquad 180^\circ - 40^\circ = 140^\circ\,.\] Больший из них равен \(140^\circ\).
В треугольнике \(ABC\): \(\angle A = 22^{\circ}\), \(\angle C = 40^{\circ}\), \(BE\) – биссектриса внешнего угла при вершине \(B\), при этом точка \(E\) лежит на продолжении стороны \(AC\). На продолжении стороны \(AB\) за точку \(B\) выбрана точка \(D\), таким образом, что \(BC = BD\). Найдите \(\angle CED\). Ответ дайте в градусах.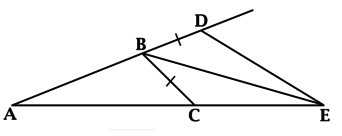
Согласно теореме о внешнем угле треугольника, \(\angle CBD = \angle A + \angle ACB = 22^{\circ} + 40^{\circ} = 62^{\circ}\).
Так как \(BE\) – биссектриса \(\angle CBD\), то \(\angle CBE = 0,5 \cdot \angle CBD = 31^{\circ}\).
\(\angle BCE = 180^{\circ} - \angle ACB = 140^{\circ}\).
Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(\angle BEC = 180^{\circ} - \angle CBE - \angle BCE = 9^{\circ}\).
Треугольники \(BCE\) и \(BDE\) равны по двум сторонам и углу между ними, тогда \(\angle CED = 2\cdot \angle BEC = 18^{\circ}\).
В треугольнике \(ABC\) точка \(M\) лежит на стороне \(AC\) (но не совпадает с точкой \(A\) или точкой \(C\)), причём \(CM = MB\). Кроме того, \(CB = MB\). Найдите сумму меньшего и большего углов треугольника \(ABC\). Ответ дайте в градусах.
Так как \(CM = MB = BC\), то треугольник \(MBC\) – равносторонний, тогда \(\angle MCB = 60^\circ\). 
Так как сумма углов треугольника равна \(180^\circ\), то угол, равный \(60^\circ\), не может быть большим и не может быть меньшим углом треугольника. Треугольник \(ABC\) не равносторонний (так как \(A\) не совпадает с \(M\)), причём \(\angle ACB = 60^\circ\), тогда один из углов \(A\) и \(B\) больше \(60^\circ\), а другой меньше \(60^\circ\). Таким образом, \[\angle A + \angle B = 180^\circ - 60^\circ = 120^\circ\] – искомая сумма углов.
В треугольнике \(ABC\) на стороне \(BC\) отмечена точка \(D\), на отрезке \(AD\) выбрана точка \(E\) так, что \(\angle BAD = \angle ECD = \angle EAC + \angle ECA\). Внешний угол при вершине \(B\) равен \(138^{\circ}\). Найдите \(\angle BAD\). Ответ дайте в градусах.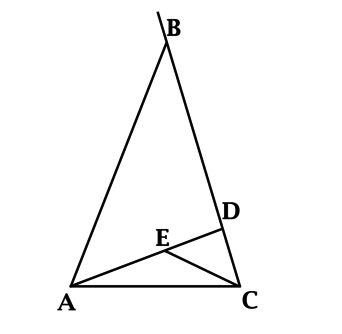
Согласно теореме о внешнем угле треугольника, внешний угол в треугольнике равен сумме двух углов треугольника, не смежных с ним.
\(\angle ADB\) – внешний для треугольника \(ADC\), тогда \(\angle ADB = \angle EAC + \angle ECA + \angle ECD = 2\cdot \angle ECD = 2\cdot \angle BAD\).
Внешний угол при вершине \(B\) равен \(\angle BAD + \angle ADB = 3\cdot \angle BAD = 138^{\circ}\), тогда \(\angle BAD = 138^{\circ} : 3 = 46^{\circ}\).
В треугольнике \(ABC\) при вершинах \(A, B\) и \(C\) построено по одному внешнему углу. Найдите сумму этих внешних углов. Ответ дайте в градусах.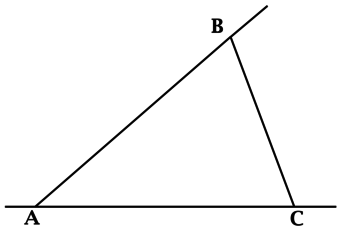
Согласно теореме о внешнем угле треугольника, внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. Тогда внешний угол при вершине \(A\) равен \(\angle B + \angle C\) в треугольнике \(ABC\).
Аналогично внешний угол при вершине \(B\) равен \(\angle A + \angle C\) в треугольнике \(ABC\), внешний угол при вершине \(C\) равен \(\angle A + \angle B\) в треугольнике \(ABC\).
Таким образом, сумма внешних углов равна \(\angle B + \angle C + \angle A + \angle C + \angle A + \angle B = 2(\angle A + \angle B + \angle C)\) в треугольнике \(ABC\), но эта сумма есть удвоенная сумма углов треугольника.
Так как сумма углов треугольника равна \(180^{\circ}\), то сумма внешних углов равна \(180^{\circ} \cdot 2 = 360^{\circ}\).
Острый угол \(B\) прямоугольного треугольника \(ABC\) равен \(55^\circ\). Найдите угол между высотой \(CH\) и медианой \(CM\), проведенными из вершины прямого угла \(C\). Ответ дайте в градусах.
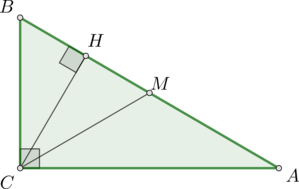
Так как медиана, опущенная из вершины прямого угла треугольника, равна половине гипотенузы, то \(\triangle BMC\) – равнобедренный, то есть \(BM=CM\). Следовательно, \(\angle BCM=\angle B=55^\circ\).
\(\angle BCH=90^\circ-\angle B=35^\circ\). Следовательно, \(\angle
HCM=55^\circ-35^\circ=20^\circ\).



