Равнобедренные и равносторонние треугольники (страница 2)
Готовиться с нами - ЛЕГКО!

Основные теоремы:
\(\blacktriangleright\) Вертикальные углы равны, а смежные в сумме дают \(180^\circ\): \(\alpha +\beta =180^\circ\).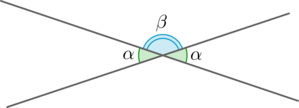
\(\blacktriangleright\) Сумма внутренних углов треугольника равна \(180^\circ\): \(\alpha+\beta+\gamma =180^\circ\)
\(\blacktriangleright\) Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: \(\phi=\alpha+\beta\)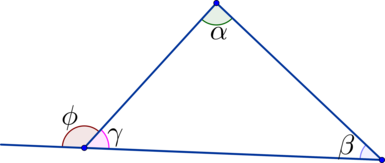
\(\blacktriangleright\) Биссектриса треугольника – отрезок, выходящий из вершины угла и делящий этот угол пополам.
\(\blacktriangleright\) Высота треугольника – отрезок, выходящий из вершины угла под углом \(90^\circ\) к противолежащей стороне (или ее продолжению).
\(\blacktriangleright\) Медиана треугольника – отрезок, выходящий из вершины угла и делящий противолежащую сторону пополам.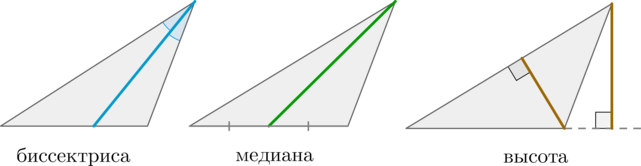
\(\blacktriangleright\) В равнобедренном треугольнике углы при основании равны.
В треугольнике \(ABC\): \(\angle B = 73^{\circ}\), \(AB = BC\). Найдите \(\angle C\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(180^{\circ} = 73^{\circ} + \angle A + \angle C = 73^{\circ} + 2\cdot \angle A\), откуда \(2\cdot \angle A = 107^{\circ}\), тогда \(\angle A = 53,5^{\circ}\).
В треугольнике \(ABC\): \(\angle B = 32^{\circ}\), \(AB = BC\). Найдите внешний угол при вершине \(C\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle ACB\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(180^{\circ} = 32^{\circ} + \angle A + \angle C = 32^{\circ} + 2\angle A\), откуда \(2\angle A = 148^{\circ}\), тогда \(\angle A = 74^{\circ}\).
По теореме о внешнем угле треугольника \(C_{\text{внеш}} = \angle A + \angle B\), тогда искомый угол равен \(32^{\circ} + 74^{\circ} = 106^{\circ}\).
В треугольнике \(ABC\): \(\angle B = 50^{\circ}\), \(AB = BC\). Найдите внешний угол при вершине \(A\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle BAC = \angle C\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(180^{\circ} = 50^{\circ} + \angle A + \angle C = 50^{\circ} + 2\angle C\), откуда \(2\angle C = 130^{\circ}\), тогда \(\angle C = 65^{\circ}\).
По теореме о внешнем угле треугольника \(A_{\text{внеш}} = \angle B + \angle C\), тогда искомый угол равен \(50^{\circ} + 65^{\circ} = 115^{\circ}\).
В треугольнике \(ABC\): \(\angle B = 39^{\circ}\), \(AB = BC\). Найдите внешний угол при вершине \(A\). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle BAC = \angle C\). Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(180^{\circ} = 39^{\circ} + \angle A + \angle C = 39^{\circ} + 2\angle C\), откуда \(2\angle C = 141^{\circ}\), тогда \(\angle C = 70,5^{\circ}\).
По теореме о внешнем угле треугольника \(A_{\text{внеш}} = \angle B + \angle C\), тогда искомый угол равен \(39^{\circ} + 70,5^{\circ} = 109,5^{\circ}\).
В треугольнике \(ABC\): \(AB = BC\), внешний угол при вершине \(C\) равен \(108^{\circ}\). Найдите \(\angle B\). Ответ дайте в градусах.
Так как градусная мера развёрнутого угла равна \(180^{\circ}\), то \(\angle ACB = 180^{\circ} - 108^{\circ} = 72^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle ACB = 72^{\circ}\).
Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - \angle A - \angle ACB = 36^{\circ}\).
В треугольнике \(ABC\): \(AB = BC\), внешний угол при вершине \(A\) равен \(112^{\circ}\). Найдите \(\angle B\). Ответ дайте в градусах.
Так как градусная мера развёрнутого угла равна \(180^{\circ}\), то \(\angle BAC = 180^{\circ} - 112^{\circ} = 68^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle C = \angle BAC = 68^{\circ}\).
Так как у любого треугольника сумма углов равна \(180^{\circ}\), то \(\angle B = 180^{\circ} - \angle BAC - \angle C = 44^{\circ}\).
В треугольнике \(ABC\): \(AB = BC\), внешний угол при вершине \(B\) равен \(104^{\circ}\). Найдите \(\angle A\). Ответ дайте в градусах.
Согласно теореме о внешнем угле треугольника, \(\angle A + \angle C = 104^{\circ}\).
В равнобедренном треугольнике углы при основании равны, тогда \(\angle A = \angle C\).
Таким образом, \(\angle A = 104^{\circ} : 2 = 52^{\circ}\).



