Равнобедренные и равносторонние треугольники (страница 5)
Готовиться с нами - ЛЕГКО!

Основные теоремы:
\(\blacktriangleright\) Вертикальные углы равны, а смежные в сумме дают \(180^\circ\): \(\alpha +\beta =180^\circ\).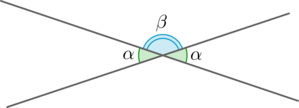
\(\blacktriangleright\) Сумма внутренних углов треугольника равна \(180^\circ\): \(\alpha+\beta+\gamma =180^\circ\)
\(\blacktriangleright\) Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: \(\phi=\alpha+\beta\)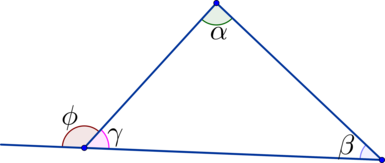
\(\blacktriangleright\) Биссектриса треугольника – отрезок, выходящий из вершины угла и делящий этот угол пополам.
\(\blacktriangleright\) Высота треугольника – отрезок, выходящий из вершины угла под углом \(90^\circ\) к противолежащей стороне (или ее продолжению).
\(\blacktriangleright\) Медиана треугольника – отрезок, выходящий из вершины угла и делящий противолежащую сторону пополам.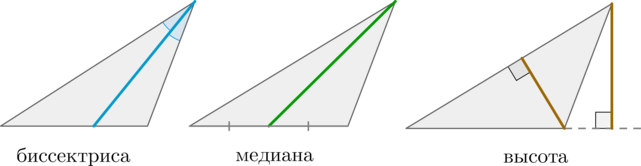
\(\blacktriangleright\) В равнобедренном треугольнике углы при основании равны.
В треугольнике \(ABC\): \(\angle A = 35^{\circ}\), \(BD\) – высота, \(\angle CBD = 26^{\circ}\). Найдите \(\angle ABC\). Ответ дайте в градусах.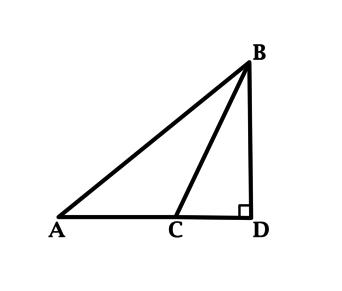
Так как \(BD\) – высота, то \(\angle ADB = 90^{\circ}\). Сумма углов треугольника равна \(180^{\circ}\), тогда \(\angle A + \angle ABD = 180^{\circ} - 90^{\circ} = 90^{\circ}\).
Так как \(\angle ABD = \angle ABC + \angle CBD\), то \(\angle ABD = \angle ABC + 26^{\circ}\). При этом \(\angle A = 35^{\circ}\), тогда \(35^{\circ} + \angle ABC + 26^{\circ} = 90^{\circ}\), откуда находим \(\angle ABC = 29^{\circ}\).
В треугольнике \(ABC\): \(\angle A = 27^{\circ}\), \(CD\) – высота, \(\angle BCD = 18^{\circ}\). Найдите \(\angle ACB\). Ответ дайте в градусах.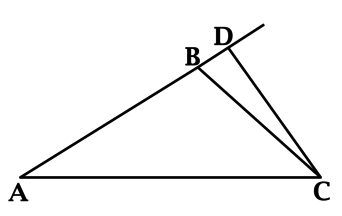
Так как \(CD\) – высота, то \(\angle ADC = 90^{\circ}\). Сумма углов треугольника равна \(180^{\circ}\), тогда \(\angle A + \angle ACD = 180^{\circ} - 90^{\circ} = 90^{\circ}\).
Так как \(\angle ACD = \angle ACB + \angle BCD\), то \(\angle ACD = \angle ACB + 18^{\circ}\). При этом \(\angle A = 27^{\circ}\), тогда \(27^{\circ} + \angle ACB + 18^{\circ} = 90^{\circ}\), откуда находим \(\angle ACB = 45^{\circ}\).
В тупоугольном треугольнике \(ABC\) один из углов равен \(47^\circ\), \(AB = 2BC\). Найдите сумму меньшего и большего углов треугольника \(ABC\). Ответ дайте в градусах.
Так как треугольник \(ABC\) – тупоугольный, то градусная мера одного из его углов больше \(90^\circ\).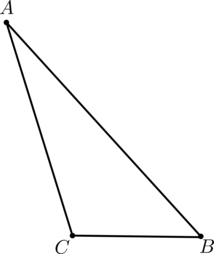
Так как сумма углов треугольника \(180^\circ\), то сумма острых углов треугольника \(ABC\) меньше \(90^\circ\), следовательно, второй острый угол в \(ABC\) меньше \(90^\circ - 47^\circ = 43^\circ\), то есть он наименьший.
Таким образом, угол в \(47^\circ\) не является ни наибольшим, ни наименьшим. В итоге сумма меньшего и большего углов треугольника \(ABC\) равна \(180^\circ - 47^\circ = 133^\circ\).
Замечание
Наличие в задаче условия \(AB = 2BC\) не влияет ни на ход решения, ни на ответ.
В треугольнике \(ABC\): \(AD\) – биссектриса, \(AC = AD = BD\). Найдите наименьший угол в треугольнике \(ABC\). Ответ дайте в градусах.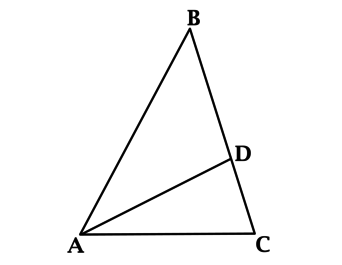
У равнобедренного треугольника углы при основании равны. Так как \(AC = AD = BD\), то \(\angle ADC = \angle C\), \(\angle B = \angle BAD\).
Согласно теореме о внешнем угле треугольника, \(\angle ADC = \angle B + \angle BAD = 2\cdot \angle B\), тогда \(\angle C = 2\cdot \angle B > \angle B\). \(\angle BAC = \angle BAD + \angle DAC = \angle B + \angle DAC > \angle B\). Таким образом, \(\angle B\) – наименьший.
Так как \(AD\) – биссектриса, то \(\angle BAC = 2\cdot \angle BAD = 2\cdot \angle B\).
Итого: \(\angle C = 2\cdot \angle B\), \(\angle BAC = 2\cdot \angle B\), значит, \(\angle BAC + \angle B + \angle C = 5\cdot \angle B\). Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(5\cdot \angle B = 180^{\circ}\), откуда находим \(\angle B = 36^{\circ}\).
В треугольнике \(ABC\): \(\angle A = 32^{\circ}\), \(\angle B = 70^{\circ}\). На продолжении стороны \(AC\) за точку \(C\) отложен отрезок \(CK = BC\). Найдите \(\angle K\) треугольника \(BCK\). Ответ дайте в градусах.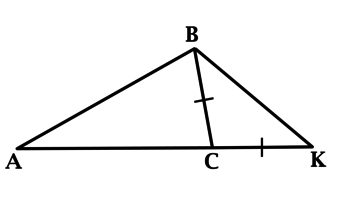
У равнобедренного треугольника углы при основании равны. Так как \(CK = BC\), то \(\angle CBK = \angle K\).
Согласно теореме о внешнем угле треугольника, \(\angle BCK = \angle A + \angle ABC = 32^{\circ} + 70^{\circ} = 102^{\circ}\).
Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(\angle BCK + \angle CBK + \angle K = 180^{\circ}\), но \(\angle CBK = \angle K\), тогда \(102^{\circ} + 2\cdot \angle K = 180^{\circ}\), откуда находим \(\angle K = 39^{\circ}\).
В треугольнике \(ABC\): \(\angle A = 52^{\circ}\), \(\angle C = 71^{\circ}\). На продолжении стороны \(BC\) за точку \(B\) отложен отрезок \(BD = AB\). Найдите \(\angle D\) треугольника \(ABD\). Ответ дайте в градусах.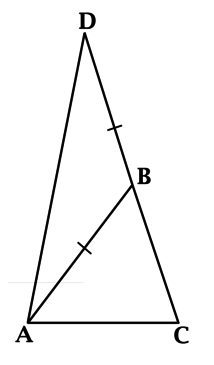
У равнобедренного треугольника углы при основании равны. Так как \(AB = BD\), то \(\angle BAD = \angle D\).
Согласно теореме о внешнем угле треугольника, \(\angle ABD = \angle C + \angle BAC = 71^{\circ} + 52^{\circ} = 123^{\circ}\).
Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(\angle D + \angle BAD + \angle ABD = 180^{\circ}\), но \(\angle BAD = \angle D\), тогда \(2\cdot \angle D + \angle ABD = 180^{\circ}\), откуда находим \(\angle D = 28,5^{\circ}\).
В треугольнике \(ABC\): \(\angle C = 40^{\circ}\), \(\angle B = 110^{\circ}\), \(AM\) – биссектриса, \(N\) – такая точка на \(AC\), что \(AB = AN\). Найдите \(\angle CMN\). Ответ дайте в градусах.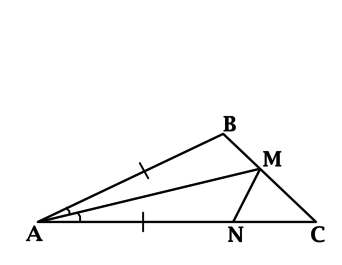
Сумма углов треугольника равна \(180^{\circ}\), тогда \(\angle BAC = 180^{\circ} - \angle B - \angle C = 180^{\circ} - 110^{\circ} - 40^{\circ} = 30^{\circ}\). Так как \(AM\) – биссектриса, то \(\angle MAN =\cdot \angle BAM = 15^{\circ}\).
Треугольники \(ABM\) и \(ANM\) равны по двум сторонам и углу между ними, тогда \(\angle BMA = \angle AMN\). \(\angle BMA = 180^{\circ} - \angle BAM - \angle B = 180^{\circ} - 15^{\circ} - 110^{\circ} = 55^{\circ}\), тогда \(\angle BMN = 2\cdot \angle BMA = 110^{\circ}\). Тогда \(\angle CMN = 180^{\circ} - 110^{\circ} = 70^{\circ}\).



