Использование различных формул площадей многоугольников (страница 2)
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Треугольник: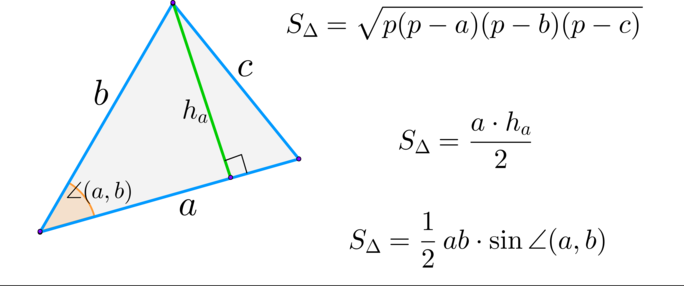
\(\blacktriangleright\) Произвольный выпуклый четырехугольник: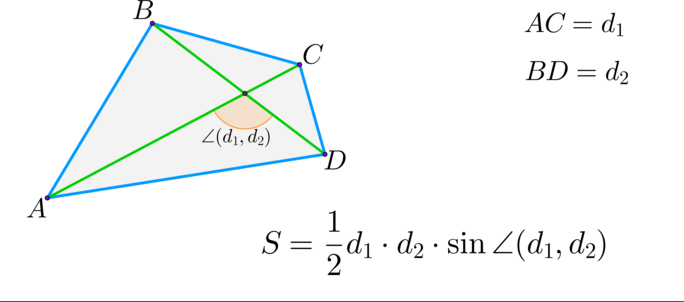
\(\blacktriangleright\) Параллелограмм: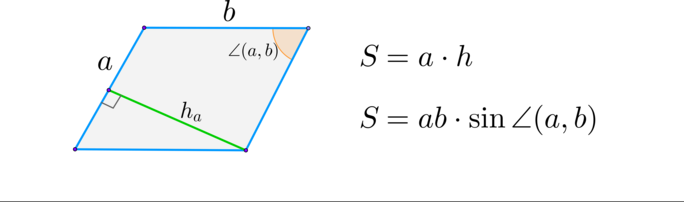
\(\blacktriangleright\) Ромб: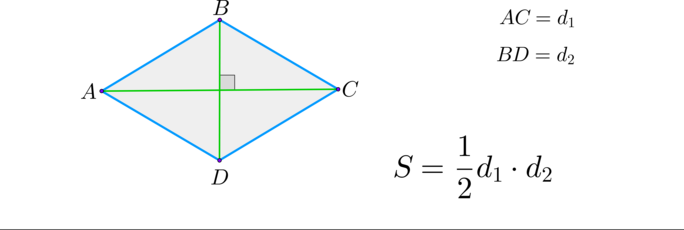
\(\blacktriangleright\) Прямоугольник:
\(\blacktriangleright\) Квадрат: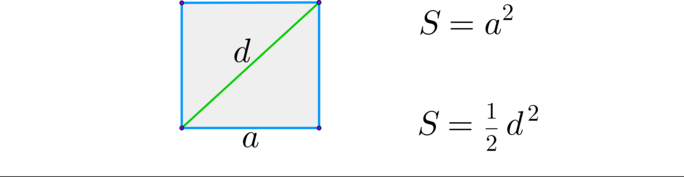
\(\blacktriangleright\) Трапеция:
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(30^\circ\). Найдите боковую сторону этого треугольника, если его площадь равна \(25\).

Пусть \(a\) – боковая сторона треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[\dfrac12\cdot a^2\cdot \sin30^\circ=S=25\quad\Rightarrow\quad
a^2=100\quad\Rightarrow\quad a=10\]
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

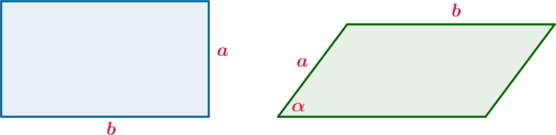
Площадь прямоугольника равна \(S_1=ab\), площадь параллелограмма равна \(S_2=ab\cdot \sin\alpha\). Из условия следует, что \(2S_2=S_1\). Следовательно: \[2ab\cdot \sin\alpha=ab\quad\Rightarrow\quad \sin\alpha=\dfrac12\quad\Rightarrow \quad \alpha=30^\circ\]
Найдите площадь треугольника, две стороны которого равны \(8\) и \(12\), а угол между ними равен \(30^\circ\).
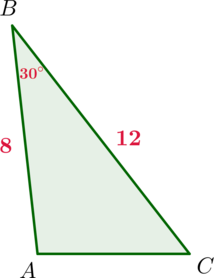
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 8\cdot 12 \cdot \dfrac12=24\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(150^\circ\). Боковая сторона треугольника равна \(20\). Найдите площадь этого треугольника.

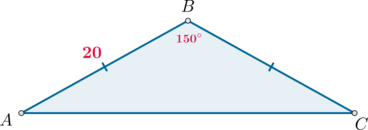
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 20^2 \cdot \dfrac12=100\]
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен \(30^\circ\). Боковая сторона треугольника равна \(10\). Найдите площадь этого треугольника.

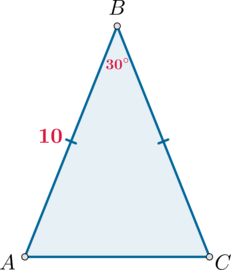
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, \[S_{ABC}=\dfrac12\cdot AB\cdot BC\cdot \sin\angle B=\dfrac12\cdot 10^2 \cdot \dfrac12=25\]
Катеты прямоугольного треугольника относятся как \(5:4\), а площадь равна \(4,1\). Найдите гипотенузу этого треугольника.
Т.к. катеты относятся как \(5:4\), то их можно обозначить за \(4x\) и \(5x\). Тогда необходимо найти гипотенузу, по теореме Пифагора равную \(\sqrt{25x^2+16x^2}=\sqrt{41x^2}\).
Т.к. площадь прямоугольного треугольника равна полупроизведению катетов, то \(S=0,5\cdot 5x\cdot 4x=10x^2=4,1\). Следовательно, \(x^2=0,41\).
Значит, гипотенуза равна \[\sqrt{41\cdot 0,41}=\sqrt{41\cdot 41\cdot 0,01}=41\cdot 0,1=4,1.\]
Дан треугольник \(ABC\). На сторонах \(AB\) и \(BC\) отмечены точки \(A'\) и \(C'\) соответственно. Известно, что \(BC'=0,5BC=4\), \(AB=14\), \(S_{ABC}=7S_{A'BC'}\). Найдите \(A'B\).

Площадь треугольника \(ABC\) равна \(S_{ABC}=0,5\cdot 14 \cdot 8\cdot \sin\angle B\).
Площадь треугольника \(A'BC'\) равна \(S_{A'BC'}=0,5\cdot A'B\cdot 4\cdot \sin\angle B\).
Таким образом, имеем равенство:
\[0,5\cdot 14 \cdot 8\cdot \sin\angle B=7\cdot 0,5\cdot A'B\cdot 4\cdot \sin\angle B \quad \Leftrightarrow \quad A'B=4.\]



