Центральные и вписанные углы окружности (страница 3)
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Центральный угол – угол, вершина которого лежит в центре окружности.
Центральный угол равен дуге, на которую он опирается.
\(\blacktriangleright\) Вписанный угол – угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую он опирается.
\(\blacktriangleright\) Таким образом, если центральный угол \(\alpha_{\text{ц}}\) и вписанный угол \(\alpha_{\text{в}}\) опираются на одну и ту же дугу, то: \[\Large{\alpha_{\text{ц}}=2\cdot
\alpha_{\text{в}}}\]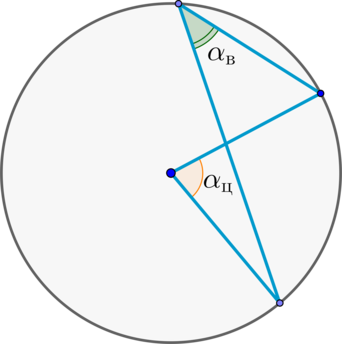
\(\blacktriangleright\) Вписанный угол, опирающийся на полуокружность (или на диаметр), равен \(90^\circ\).
Найдите величину острого вписанного угла, опирающегося на хорду, равную радиусу окружности. Ответ дайте в градусах.
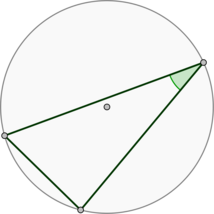
Обозначим хорду за \(AB\). Рассмотрим \(\triangle AOB\), где \(O\) – центр окружности.
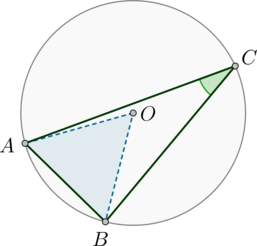
Так как \(AB\) равна радиусу окружности, то \(\triangle AOB\) – равносторонний. Следовательно, \(\angle
AOB=60^\circ\). Заметим, что \(\angle AOB\) и \(\angle ACB\) – центральный и вписанный углы, опирающиеся на одну и ту же дугу, следовательно, \(\angle ACB=0,5\angle AOB=30^\circ\).
Хорда \(CD\) перпендикулярна диаметру \(AB\). Найдите разность градусных мер дуг \(AC\) и \(AD\) (тех, которые меньше полуокружности). Ответ дайте в градусах.
Построим отрезки \(CA\), \(AD\) и \(CB\), точку пересечения \(CD\) и \(AB\) обозначим \(E\).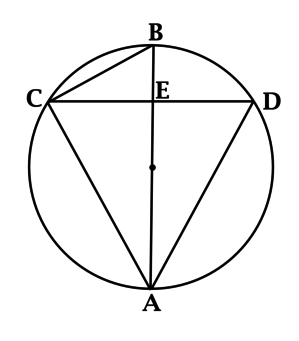
\(\angle BCD = \angle BAD\) как вписанные, опирающиеся на общую дугу. Так как \(AB\) – диаметр, то \(\angle BCA = 90^{\circ}\).
Тогда \(\angle BCD\) дополняет \(\angle DCA\) до \(90^{\circ}\), а \(\angle BAD\) дополняет \(\angle CDA\) до \(90^{\circ}\) и из равенства \(\angle BCD = \angle BAD\) вытекает \(\angle DCA = \angle CDA\), следовательно, дуги \(AC\) и \(AD\) равны.
Сторона \(AB\) тупоугольного треугольника \(ABC\) равна радиусу описанной около него окружности. Найдите тупой угол \(C\). Ответ дайте в градусах.
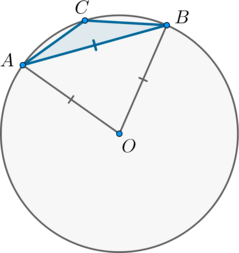
\(\triangle AOB\) равносторонний, следовательно, \(\angle
AOB=\buildrel\smile\over{AB}=60^\circ\). Тогда большая дуга \(AB\) равна \(360^\circ-60^\circ=300^\circ\). Угол \(ACB\) – вписанный угол, опирающийся на большую дугу \(AB\), следовательно, равен ее половине: \(\angle ACB=\frac12\cdot 300^\circ=150^\circ.\)
\(AB\) – диаметр окружности, который пересекает хорду \(CD\) в точке \(E\). Градусная мера дуги \(AC\) равна \(90^{\circ}\), а градусная мера дуги \(CBD\) равна \(150^{\circ}\). Найдите \(\angle CEA\). Ответ дайте в градусах.
Построим диаметр \(CF\). Пусть \(O\) – центр окружности, тогда \(\angle COA = 90^{\circ}\).
\(\angle CEA = 90^{\circ} - \angle DCF\).
Так как градусная мера дуги \(CBD\) равна \(150^{\circ}\), а \(CF\) – диаметр, то градусная мера дуги \(DF\) равна \(180^{\circ} - 150^{\circ} = 30^{\circ}\).
Вписанный угол в два раза меньше градусной меры дуги, на которую он опирается, тогда \(\angle DCF = 0,5\cdot 30^{\circ} = 15^{\circ}\), следовательно, \(\angle CEA = 90^{\circ} - 15^{\circ} = 75^{\circ}\).
На рисунке \(O\) – центр окружности, \(AO=OB=BC=CA\). Найдите угол \(ADC\). Ответ дайте в градусах.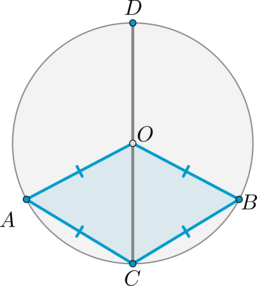
Четырехугольник, все стороны которого равны, является ромбом. Следовательно, \(AOBC\) – ромб. Значит, диагонали делят его углы пополам. Следовательно, \(\angle AOC=\angle BOC=\angle ACO=\angle BCO=x\).
Следовательно, \(\buildrel\smile\over{AC}=\buildrel\smile\over{CB}=x\) (т.к. на них опираются центральные углы \(AOC\) и \(BOC\), равные этим дугам), \(\buildrel\smile\over{AD}=\buildrel\smile\over{DB}=2x\) (т.к. на них опираются вписанные углы \(ACD\) и \(BCD\), равные половинам этих дуг).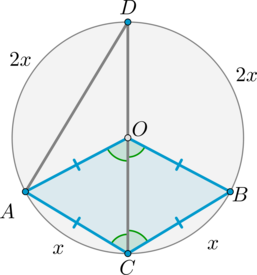
Т.к. вся окружность равна \(360^\circ\), то \(x+x+2x+2x=360^\circ \quad \Rightarrow \quad x=60^\circ\).
Угол \(ADC\) – вписанный и опирающийся на дугу \(\buildrel\smile\over{AC}\), следовательно, он равен ее половине, то есть \(30^\circ\).
Секущая \(AB\) пересекает окружность и диаметр \(CD\) так, как показано на рисунке.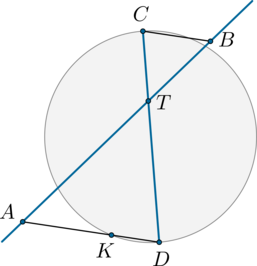
Меньшая дуга \(\buildrel\smile\over{KD}\) равна \(40^\circ\), \(\angle CBA=30^\circ\), прямая \(BC\) параллельна прямой \(AD\). Найдите угол \(BTD\). Ответ дайте в градусах.
Рассмотрим картинку: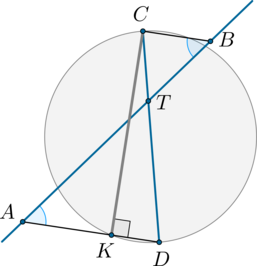
Т.к. \(BC\parallel AD\), то \(\angle CBT=\angle DAT=30^\circ\). \(\angle DCK\), как вписанный и опирающийся на дугу \(KD\), равен ее половине, то есть \(20^\circ\). \(\angle CKD\) опирается на диаметр \(CD\), следовательно, равен половине от половины окружности, то есть \(90^\circ\). Значит, \(\angle CDK=180^\circ -90^\circ -20^\circ=70^\circ\).
\(\angle BTD\) — внешний угол для треугольника \(ATD\), следовательно, он равен сумме двух углов треугольника, не смежных с ним: \(\angle BTD=\angle TDA+\angle TAD=30^\circ+70^\circ=100^\circ\).
На окружности в следующем порядке отмечены четыре точки: \(A\), \(B\), \(C\) и \(D\), причем \(AB=BC, \ CD=DA\). Найдите угол \(BAD\). Ответ дайте в градусах.
Рассмотрим картинку: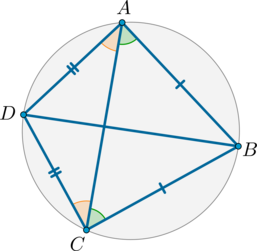
Т.к. \(\triangle BAC\) и \(DAC\) – равнобедренные, то \(\angle BAC=\angle BCA, \ \angle DAC=\angle DCA\). Таким образом, \(\angle A=\angle C\).
Т.к. \(\angle A, \angle C\) – вписанные, то \(\angle A+\angle
C=\frac12\left(\buildrel\smile\over{DCB}+\buildrel\smile\over{DAB}\right)\).
Заметим, что эти дуги в сумме дают всю окружность, то есть \(360^\circ\). Следовательно, \(\angle A+\angle C=180^\circ\), следовательно, \(\angle A=\angle C=90^\circ\).



