Окружность, описанная около многоугольника
Готовиться с нами - ЛЕГКО!

Окружность называется описанной около выпуклого многоугольника, если все вершины этого многоугольника лежат на окружности.
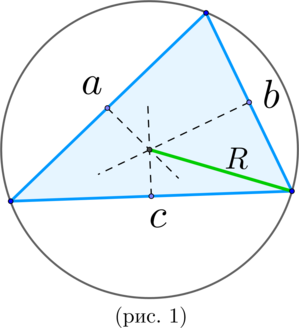
\(\blacktriangleright\) Около любого треугольника можно описать окружность. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника (рис. 1).
Для вписанного треугольника верна формула \[\dfrac{a}{\sin\alpha}=2R,\] где \(\alpha\) – угол треугольника, лежащий против стороны \(a\).
Площадь вписанного треугольника вычисляется по формуле
\[\Large{S_{\triangle}=\dfrac{abc}{4R}}\]
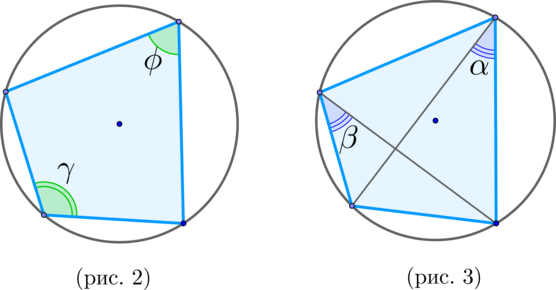
\(\blacktriangleright\) Если около выпуклого четырехугольника описана окружность, то сумма его противоположных углов равна \(\large{\angle\phi + \angle\gamma=180^\circ}\).
И наоборот: Если сумма двух противоположных углов выпуклого четырехугольника равна \(\large{\angle\phi +
\angle\gamma=180^\circ}\), то около него можно описать окружность. (рис. 2)
\(\blacktriangleright\) Около выпуклого четырехугольника описана окружность \(\Leftrightarrow\) \(\large{\angle \alpha =\angle
\beta}\). (рис. 3)
Площадь вписанного четырехугольника вычисляется по формуле
\[{\large{S_{\text{впис.4-к}}=\sqrt{(p-a)(p-b)(p-c)(p-d)},}}\]
где \(a,b,c,d\) – его стороны, \(p=\frac12(a+b+c+d)\) – полупериметр.
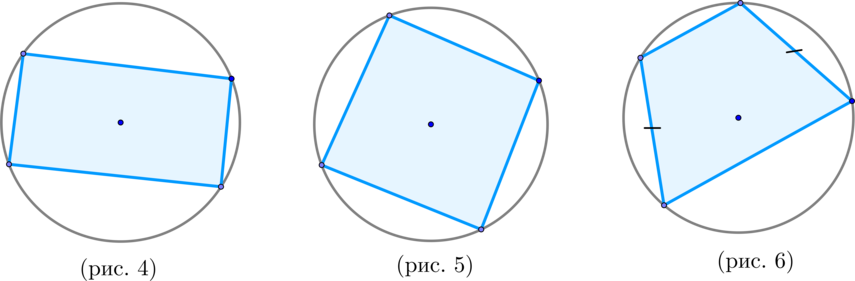
\(\blacktriangleright\) Если около параллелограмма описана окружность, то он – прямоугольник (рис. 4).
\(\blacktriangleright\) Если около ромба описана окружность, то он – квадрат (рис. 5).
\(\blacktriangleright\) Если около трапеции описана окружность, то она равнобедренная.
И наоборот: около равнобедренной (и только равнобедренной) трапеции можно описать окружность (рис. 6).
В четырёхугольнике \(ABCD\): диагонали \(AC\) и \(BD\) пересекаются в точке \(M\), \(\angle ABC + \angle ADC = 180^{\circ}\). Найдите отношение углов \(CBD\) и \(CAD\).
Если в выпуклом четырёхугольнике сумма противоположных углов равна \(180^{\circ}\), то около него можно описать окружность, тогда около \(ABCD\) можно описать окружность.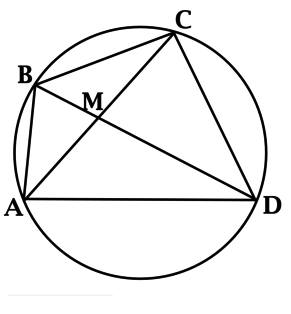
\(\angle CBD\) и \(\angle CAD\) – вписанные, опирающиеся на одну дугу, тогда они равны и их отношение равно 1.
В выпуклом четырехугольнике \(ABCD\) \(\angle ABD=\angle ACD\). Найдите \(\angle A-\angle B+\angle C-\angle D\). Ответ дайте в градусах.
Рассмотрим картинку: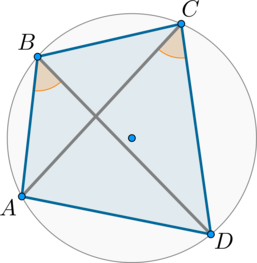
По признаку около этого четырехугольника можно описать окружность. Следовательно, сумма двух противоположных его углов равна \(180^\circ\). Таким образом, \[\angle A-\angle B+\angle C-\angle D= (\angle A+\angle C)-(\angle B+\angle D)=180^\circ-180^\circ=0^\circ.\]
Около трапеции описана окружность. Периметр трапеции равен \(22\), средняя линия равна \(5\). Найдите боковую сторону трапеции.

Так как трапеция вписана в окружность, то трапеция является равнобедренной, следовательно, \(AB=CD\). Средняя линия равна полусумме оснований, следовательно, \(AD+BC=2\cdot 5=10\). Тогда \[AB+BC+CD+AD=10+2AB=22\quad\Rightarrow\quad AB=6.\]
Сторона правильного треугольника равна \(\sqrt3\). Найдите радиус окружности, описанной около этого треугольника.
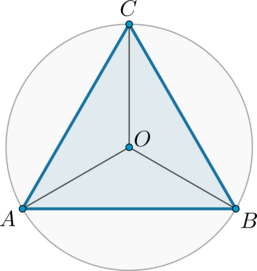
По теореме синусов \[\dfrac a{\sin \alpha}=2R\] где \(a\) – сторона треугольника, \(\alpha\) – противолежащий этой стороне угол, \(R\) – радиус описанной окружности. Так как в правильном треугольнике все углы равны по \(60^\circ\), то \[2R=\dfrac {\sqrt3}{\sin60^\circ}=\dfrac{\sqrt3}{\frac{\sqrt3}2}=2 \quad\Rightarrow\quad R=1\]
Стороны \(AB, BC, CD, AD\) четырехугольника \(ABCD\) стягивают дуги описанной окружности, градусные меры которых равны соответственно \(95^\circ, 49^\circ, 71^\circ, 145^\circ\). Найдите угол \(B\) этого четырехугольника. Ответ дайте в градусах.
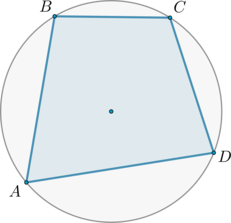
Угол \(B\) четырехугольника равен вписанному углу \(ABC\). Этот угол опирается на дугу \(\buildrel\smile\over{ADC}\), равную \(145^\circ+71^\circ=216^\circ\). Так как вписанный угол равен половине дуги, на которую он опирается, то \(\angle B=\angle ABC=108^\circ\).
Точки \(A, B, C, D\), расположенные на окружности, делят эту окружность на четыре дуги \(AB, BC, CD, DA\), градусные величины которых относятся соответственно как \(4:2:3:6\). Найдите угол \(A\) четырехугольника \(ABCD\). Ответ дайте в градусах.

Так как дуги \(AB, BC, CD, DA\) относятся как \(4:2:3:6\), то можно принять дугу \(AB\) за \(4x\), дугу \(BC\) за \(2x\), дугу \(CD\) за \(3x\) и дугу \(DA\) за \(6x\). Так как все эти дуги в совокупности дают целую окружность, градусная мера которой равна \(360^\circ\), то \(4x+2x+3x+6x=360^\circ\), откуда \(x=24^\circ\).
Угол \(A\) равен вписанному углу \(BAD\), опирающемуся на дугу \(\buildrel\smile\over{BCD}\), равную \(2x+3x=5x=120^\circ\). Так как вписанный угол равен половине этой дуги, то \(\angle A=60^\circ\).
Четырехугольник \(ABCD\) вписан в окружность. Угол \(ABC\) равен \(110^\circ\), угол \(ABD\) равен \(70^\circ\). Найдите угол \(CAD\). Ответ дайте в градусах.
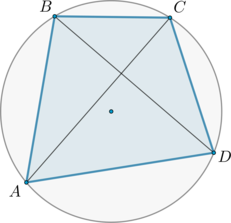
Вписанные углы, опирающиеся на равные дуги, равны. Следовательно, \(\angle CAD=\angle CBD\).
\(\angle CBD=\angle ABC-\angle ABD=110^\circ-70^\circ=40^\circ\).
Тема «Окружность, описанная около правильного многоугольника» довольно подробно рассматривается в рамках школьной программы. Несмотря на это, задания, относящиеся к данному разделу планиметрии, вызывают у многих старшеклассников определенные сложности. При этом понимать принцип решения задач ЕГЭ с окружностью, описанной около многоугольника, должны выпускники с любым уровнем подготовки.
Как подготовиться к единому госэкзамену?
Для того чтобы задания ЕГЭ по теме «Окружность, описанная около правильного многоугольника» не вызывали у учащихся затруднений, занимайтесь вместе с образовательным порталом «Школково». С нами вы сможете повторить теоретический материал по темам, которые вызывают у вас трудности. Теоремы и формулы, которые раньше казались достаточно сложными, у нас изложены доступно и понятно.
Чтобы освежить в памяти основные определения и понятия об углах и центре окружности, описанной около многоугольника, а также теоремы, связанные с длинами отрезков, выпускникам достаточно перейти в раздел «Теоретическая справка». Здесь мы разместили материал, составленный нашими опытными сотрудниками специально для учащихся с различным уровнем подготовки.
Чтобы закрепить усвоенную информацию, старшеклассники могут попрактиковаться в выполнении упражнений. На образовательном портале «Школково» в разделе «Каталог» представлена большая база задач различной сложности для максимально эффективной подготовки к ЕГЭ. В каждом задании на сайте прописан алгоритм решения и дан правильный ответ. База упражнений «Школково» регулярно обновляется и дополняется.
Практиковаться в выполнении задач на нашем сайте учащиеся из Москвы и других российских городов могут в онлайн-режиме. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». В дальнейшем к этому заданию можно будет вернуться и, к примеру, обсудить алгоритм его решения со школьным преподавателем или репетитором.



