Четные и нечетные функции (страница 2)
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Функция \(f(x)\) называется четной, если при всех \(x\) из ее области определения верно: \(f(-x)=f(x)\).
График четной функции симметричен относительно оси \(y\):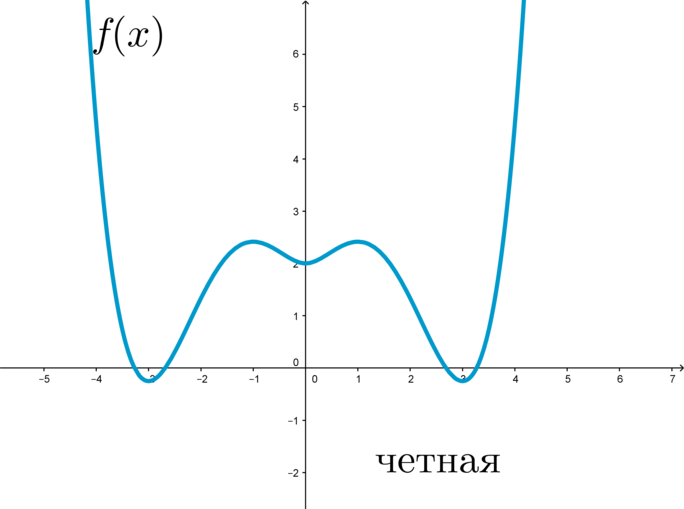
Пример: функция \(f(x)=x^2+\cos x\) является четной, т.к. \(f(-x)=(-x)^2+\cos{(-x)}=x^2+\cos x=f(x)\).
\(\blacktriangleright\) Функция \(f(x)\) называется нечетной, если при всех \(x\) из ее области определения верно: \(f(-x)=-f(x)\).
График нечетной функции симметричен относительно начала координат: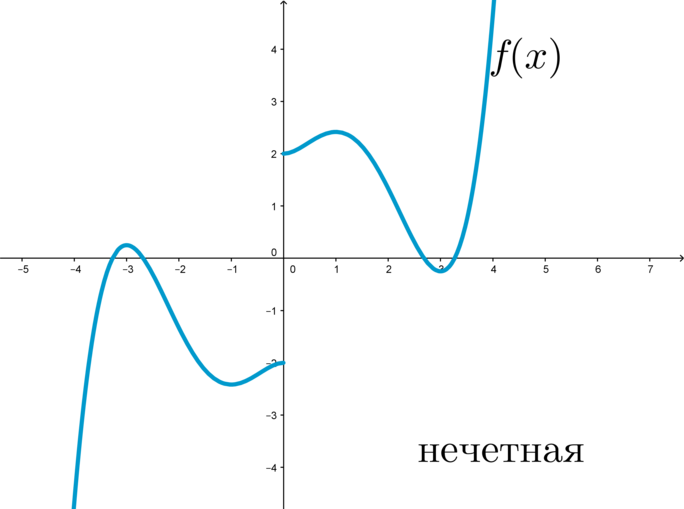
Пример: функция \(f(x)=x^3+x\) является нечетной, т.к. \(f(-x)=(-x)^3+(-x)=-x^3-x=-(x^3+x)=-f(x)\).
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
Например, функция \(f(x)=x^2-x\) является суммой четной функции \(f_1=x^2\) и нечетной \(f_2=-x\).
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
5) Если \(f(x)\) — четная функция, то уравнение \(f(x)=c \ (c\in
\mathbb{R}\)) имеет единственный корень тогда и только когда, когда \(x=0\).
6) Если \(f(x)\) — четная или нечетная функция, и уравнение \(f(x)=0\) имеет корень \(x=b\), то это уравнение обязательно будет иметь второй корень \(x=-b\).
\(\blacktriangleright\) Функция \(f(x)\) называется периодической на \(X\), если для некоторого числа \(T\ne 0\) выполнено \(f(x)=f(x+T)\), где \(x,
x+T\in X\). Наименьшее \(T\), для которого выполнено данное равенство, называется главным (основным) периодом функции.
У периодической функции любое число вида \(nT\), где \(n\in \mathbb{Z}\) также будет являться периодом.
Пример: любая тригонометрическая функция является периодической;
у функций \(f(x)=\sin x\) и \(f(x)=\cos x\) главный период равен \(2\pi\), у функций \(f(x)=\mathrm{tg}\,x\) и \(f(x)=\mathrm{ctg}\,x\) главный период равен \(\pi\).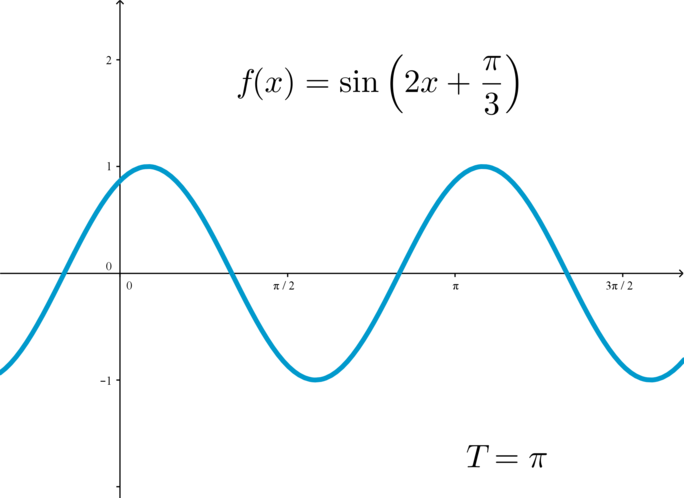
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево: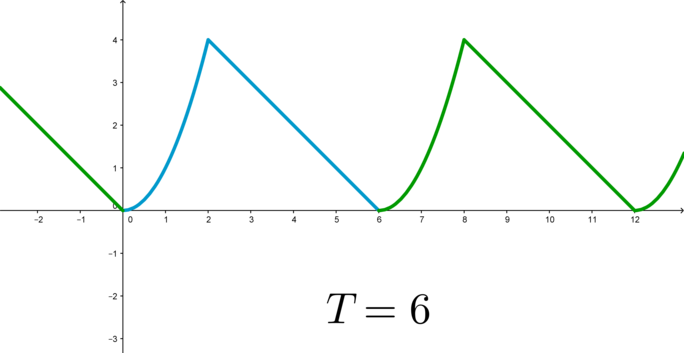
\(\blacktriangleright\) Область определения \(D(f)\) функции \(f(x)\) — это множество, состоящее из всех значений аргумента \(x\), при которых функция имеет смысл (определена).
Пример: у функции \(f(x)=\sqrt x+1\) область определения: \(x\in
[0;+\infty)\).
\(\blacktriangleright\) Область значений \(E(f)\) функции \(f(x)\) — это множество, состоящее из всех значений функции \(f(a)\), где \(a\in
D(f)\).
Пример: у функции \(f(x)=\sqrt x +1\) область значений: \(f(x)\in
[1;+\infty)\).
\(\blacktriangleright\) Уравнение \(f(x)=a\) имеет решение тогда и только тогда, когда \(a\) принадлежит области значений функции \(f(x)\), т.е. \(a\in E(f)\).
\(\blacktriangleright\) Если область значений функции \(f(x)\) не превышает некоторого числа \(A\), т.е. \(f(x)\leq A\) при всех \(x\in D(f)\), а функция \(g(x)\geq A\) при всех \(x\in D(g)\), то уравнение \[{\large{f(x)=g(x)}} \Leftrightarrow \begin{cases} f(x)=A\\g(x)=A\end{cases}\]
При каких значениях параметра \(a\) уравнение
\[\cos x+\dfrac32 \cos \dfrac{2x}3+3\cos \dfrac x3=a\]
имеет решения.
1) Рассмотрим функцию \(f(x)=\cos x+\frac32 \cos \frac{2x}3+3\cos
\frac x3\).
Главный период у \(\cos x\) – это \(2\pi\),
у \(\cos \frac{2x}3\) — это \(\dfrac{2\pi}{\frac23}=3\pi\),
у \(\cos\frac x3\) – это \(\dfrac{2\pi}{\frac13}=6\pi\).
Тогда главный период всей функции \(f(x)\) – это НОК этих периодов, то есть \(6\pi\).
2) Для того, чтобы уравнение имело решения, необходимо, чтобы на любом отрезке длиной \(6\pi\) выполнялось: \(\mathrm{min}\,f(x)\leqslant a\leqslant \mathrm{max}\,f(x)\). Возьмем, например, отрезок \([0;6\pi]\).
3) Найдем критические точки функции и построим ее схематичный график для того, чтобы понять, чему равно \(\mathrm{min}\,f(x)\) и \(\mathrm{max}\,f(x)\).
\(f'(x)=\sin x+\sin \dfrac{2x}3+\sin \dfrac x3=0\quad \Rightarrow \quad \left(\sin x+\sin \dfrac{x}3\right)+\sin \dfrac{2x}3=0 \quad \Rightarrow\)
\(\Rightarrow \quad 2\sin \dfrac{2x}3\cos \dfrac x3+\sin \dfrac{2x}3=0 \quad \Rightarrow \quad \sin \dfrac{2x}3\left(2\cos \dfrac x3+1\right)=0\quad \Rightarrow \)
\(\Rightarrow \quad \left[ \begin{gathered} \begin{aligned} &\dfrac{2x}3=\pi n, n\in\mathbb{Z}\\[3pt] & \dfrac x3=\pm \dfrac{2\pi}3+2\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered} \right. \quad \Rightarrow \quad \left[ \begin{gathered} \begin{aligned} &x=\dfrac32\pi n, n\in\mathbb{Z}\\[3pt] &x=\pm 2\pi+6\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered} \right.\)
Промежутку \([0;6\pi]\) принадлежат точки \(0;\ \frac{3\pi}2;\ 2\pi;\
3\pi;\ 4\pi; \ \frac{9\pi}2;\ 6\pi\). Значит, знаки производной такие:
Значит, минимальное значение на \([0;6\pi]\) функция принимает в одной из точек \(\frac{3\pi}2;\ 3\pi;\ \frac{9\pi}2\), а максимальное — в одной из \(0;\ 2\pi;\ 4\pi; \ 6\pi\).
\(\begin{aligned} &f(0)=f(6\pi)=\dfrac{11}2\\[4pt] &f\left(\dfrac{3\pi}2\right)=f\left(\dfrac{9\pi}2\right)=-\dfrac32\\[4pt] &f(2\pi)=f(4\pi)=-\dfrac54\\[4pt] &f(3\pi)=-\dfrac52 \end{aligned}\)
Тогда на \([0;6\pi]\) схематично функция выглядит так:
То есть \(\mathrm{min}\,f(x)=-\dfrac52, \ \mathrm{max}\,f(x)=\dfrac{11}2\). Значит, \(a\in\left[-\dfrac52;\dfrac{11}2\right]\).
\(a\in \left[-\dfrac52;\dfrac{11}2\right]\)
Найдите все значения параметра \(a\), при которых уравнение \[x^4+12|x-2|+9=\dfrac{7}{3}x^3 +x^2 +7|x-11a|\]
имеет более одного корня.
Перепишем уравнение в другом виде:
\[x^4-\dfrac{7}{3}x^3-x^2+9=7|x-11a|-12|x-2|\]
Пусть \(f(x)=x^4-\dfrac{7}{3}x^3-x^2+9, \ \ g(x)=7|x-11a|-12|x-2|\)
Изобразим графики обеих функций:
1)\(f(x)=x^4-\dfrac{7}{3}x^3-x^2+9 \Longrightarrow f'(x)=4x^3-7x^2-2x\)
\[f'(x)=0 \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=-\dfrac{1}{4}\\ &x=0\\ &x=2 \end{aligned} \end{gathered} \right.\]
\(x=-\dfrac{1}{4}\) и \(x=2\) – точки минимума, \(x=0\) – точка максимума.
Причем \(f\left(-\dfrac{1}{4}\right)=\dfrac{6895}{768}>f(2)=\dfrac{7}{3}\)
2)\(g(x)=7|x-11a|-12|x-2|\)
Рассмотрим два случая:
2.1) \(x\geqslant 2\). Тогда \(|x-2|=x-2\). В этом случае вне зависимости от того, как раскроется модуль \(|x-11a|\), \(g(x)\) – линейная функция, коэффициент перед \(x\) у которой будет отрицательным (в точности, он будет равен \(-19\) или \(-5\)). Т.е. \(g(x)\) всегда убывает при \(x\geqslant
2\).
2.2) \(x<2\). Тогда \(|x-2|=-(x-2)\). В этом случае вне зависимости от того, как раскроется модуль \(|x-11a|\), \(g(x)\) – линейная функция, коэффициент перед \(x\) у которой будет положительным (в точности, он будет равен \(19\) или \(5\)). Т.е. \(g(x)\) всегда возрастает при \(x< 2\).
Таким образом, \(x=2\) – точка максимума (единственная) у функции \(g(x)\), причем \(g(2)=7|2-11a|\)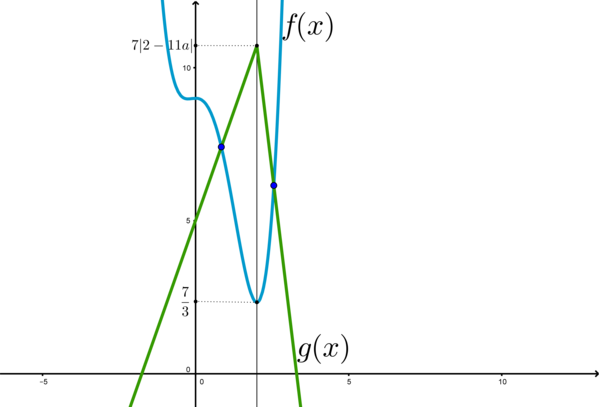
Уравнение будет иметь более одного корня, если \(g(2)>f(2)\).
Решая данное неравенство, получим \(a\in \left(-\infty; \dfrac{5}{33}\right)\cup \left(\dfrac{7}{33};+\infty\right)\).
\(a\in \left(-\infty; \dfrac{5}{33}\right)\cup \left(\dfrac{7}{33};+\infty\right)\).
Найдите все значения параметра \(a\), при каждом из которых уравнение \[x^2-|x+a+3|=|x-a-3|-(a+3)^2\]
имеет единственное решение.
(Задача от подписчиков)
Перенесем все слагаемые в левую часть: \[x^2-|x+a+3|-|x-a-3|+(a+3)^2=0\] Рассмотрим функцию: \(f(x)=x^2-|x+a+3|-|x-a-3|+(a+3)^2\). Данная функция определена при всех \(x\in \mathbb{R}\) и является четной, так как \(f(x)=f(-x)\). Следовательно, для каждого \(x_0>0\), удовлетворяющего уравнению, существует также корень \(-x_0\), удовлетворяющий уравнению. Следовательно, для того, чтобы уравнение имело единственный корень, его корнем должен быть только \(x=0\).
Подставим \(x=0\): \[-|a+3|-|-a-3|+(a+3)^2=0 \quad\Rightarrow\quad (a+3)^2-2|a+3|=0\] Сделав замену \(t=|a+3|\), сведем уравнение к виду \(t^2-2t=0\); корнями будут \(t=0\) и \(t=2\). Следовательно, \[\left[ \begin{gathered}\begin{aligned}
&|a+3|=0\\
&|a+3|=2 \end{aligned} \end{gathered}
\right.\quad\Leftrightarrow\quad \left[
\begin{gathered}\begin{aligned}
&a=-3\\
&a=-1\\
&a=-5 \end{aligned} \end{gathered} \right.\]
Проверим, действительно ли при этих значениях \(a\) уравнение имеет только корень \(x=0\).
1) Подставим \(a=-3\): \[x^2-|x|-|x|=0 \quad\Leftrightarrow\quad x^2-2|x|=0\] Данное уравнение имеет корни: \(x=0; 2; -2\). Следовательно, \(a=-3\) не подходит.
2) Подставим \(a=-1\): \[x^2-|x+2|-|x-2|+4=0 \quad\Leftrightarrow\quad x^2+4=|x+2|+|x-2|\] Решим данное уравнение графически:
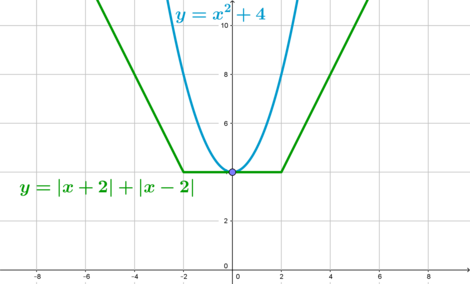
Убеждаемся, что уравнение действительно имеет ровно один корень.
3) Подставив \(a=-5\), получаем то же уравнение, что и при \(a=-1\).
Таким образом, окончательный ответ: \[a\in \{-5;-1\}\]
\(\{-5;-1\}\)
Найдите все значения параметра \(a\), при которых уравнение \[2\sqrt{x^2+4x+20}=5a-a^2+2|x-2a+2|-11|x+2|\]
имеет решения.
Сделаем замену: \(x+2=t\). Для того, чтобы исходное уравнение имело хотя бы одно решение, необходимо и достаточно, чтобы полученное уравнение \[2\sqrt{t^2+16}=5a-a^2+2|t-2a|-11|t|\] имело хотя бы одно решение.
1 способ.
1) \(a<0\). Модули раскрываются следующим образом:
\[2\sqrt{t^2+16}=\begin{aligned} \begin{cases} 9a-a^2+9t,
\qquad &{\small{\text{если }}}\quad t<2a\\
a-a^2+13t, \qquad &{\small{\text{если }}}\quad 2a\leqslant t\leqslant 0\\
a-a^2-9t, \qquad &{\small{\text{если }}}\quad t>0
\end{cases}\end{aligned} \qquad \qquad (*)\]
Изобразим схематично график системы \((*)\), причем заметим, что при \(a<0\): \[g(2a)=27a-a^2<0, \quad g(0)=a-a^2<0.\]
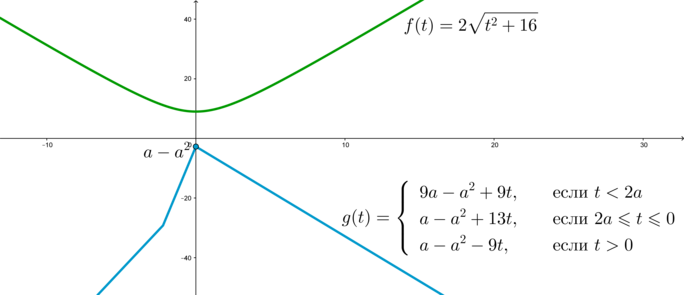
Из графика видно, что уравнение ни при каких \(a<0\) не имеет решений.
2) \(a=0\). Тогда уравнение примет вид \[2\sqrt{t^2+16}=-9|t|\] Левая часть этого уравнения всегда положительна, а правая – всегда неположительна. Следовательно, данное уравнение не имеет решений.
3) \(a>0\). Тогда модули раскрываются следующим образом:
\[2\sqrt{t^2+16}=\begin{aligned}
\begin{cases}
9a-a^2+9t, \qquad &{\small{\text{если }}}\quad t<0\\
9a-a^2-13t, \qquad &{\small{\text{если }}}\quad 0\leqslant t\leqslant 2a\\
a-a^2-9t, \qquad &{\small{\text{если }}}\quad t>2a
\end{cases}\end{aligned} \qquad
\qquad (**)\]
Изобразим схематично график системы \((**)\), причем заметим, что при \(a>0\): \[g(0)=9a-a^2, \quad g(2a)=-a^2-17a<0.\]
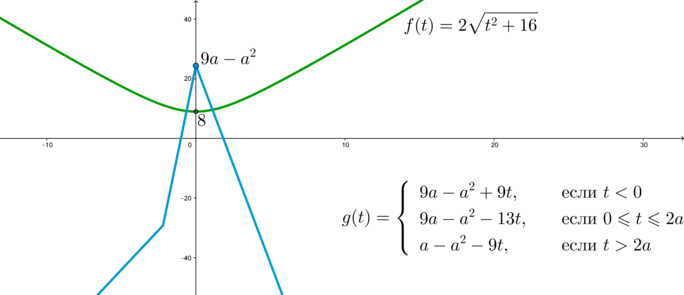
Уравнение будет иметь хотя бы один корень, когда вершина графика функции \(g(t)\) будет не ниже вершины графика функции \(f(t)\): \[9a-a^2\geqslant 8 \quad\Leftrightarrow\quad a\in [1;8].\] Данные значения для \(a\) подходят под условие \(a>0\).
2 способ. \[2\sqrt{t^2+16}=5a-a^2+2|t-2a|-11|t|\]
Рассмотрим два случая:
1) \(t\geqslant 0\). Тогда \(|t|=t\). В этом случае вне зависимости от того, как раскроется модуль \(|t-2a|\), справа будет стоять линейная функция, коэффициент перед \(t\) у которой будет отрицательным (в точности, он будет равен или \(-13\), или \(-9\)). То есть функция справа будет всегда убывать.
2) \(t<0\). Тогда \(|t|=-t\). В этом случае вне зависимости от того, как раскроется модуль \(|t-2a|\), справа будет стоять линейная функция, коэффициент перед \(t\) у которой будет положительным (в точности, он будет равен или \(13\), или \(9\)). То есть функция справа будет всегда возрастать.
Таким образом, точка максимума у функции справа – это \(t=0\), и в этой точке значение функции равно \(5a-a^2+2|-2a|=5a-a^2+4|a|\).
Рассмотрим функцию слева: она всегда положительна, имеет единственный минимум в точке \(t=0\), и в этой точке значение функции равно \(8\) (до точки \(t=0\) она убывает, после – возрастает).
Следовательно, уравнение будет иметь решения в том случае, если \[5a-a^2+4|a|\geqslant 8\]Решая данное неравенство, получаем тот же ответ \(a\in [1;8].\)
\([1;8]\)
Найти все значения \(a\), при каждом из которых уравнение
\[|\log_{0,5}x^2-a|-|\log_{0,5}x+2a|=(\log_{0,5}x)^2\]
имеет хотя бы один корень, меньший \(2\).
1) ОДЗ данного уравнения: \(x>0\). Следовательно, на ОДЗ верно: \(\log_{0,5}x^2=2\log_{0,5}x\). Сделаем замену \(\log_{0,5}x=t\). Тогда если уравнение относительно \(x\) должно иметь хотя бы один корень, меньший 2, то относительно \(t\) уравнение должно иметь хотя бы один корень, больший \(-1\).
Действительно, \(\log_{0,5}x=-\log_2x\), следовательно, если \(x<2\), то \(\log_2x<\log_22\) (потому как функция \(y=\log_2x\) возрастает), значит, \(-\log_2x>-\log_22=-1\).
Таким образом, нужно, чтобы уравнение
\[|2t-a|-|t+2a|=t^2 \qquad \qquad (*)\]
имело хотя бы один корень, больший \(-1\).
2) Каждый модуль может раскрыться одним из двух способов: либо положительно, либо отрицательно. Значит, два модуля могут раскрыться одним из четырех способов. Рассмотрим все эти четыре случая:
I) \(2t-a\geqslant 0\) и \(t+2a\geqslant 0\). Тогда \(|2t-a|=2t-a, \ |t+2a|=t+2a\). Тогда уравнение примет вид:
\[2t-a-t-2a=t^2 \quad \Leftrightarrow \quad a=-\dfrac13\left(t^2-t\right)\]
Рассмотрим прямоугольную систему координат (\(t\) на месте оси абсцисс, \(a\) на месте оси ординат). Область, соответствующая \(2t-a\geqslant 0 \quad \Rightarrow \quad a\leqslant 2t\), — это часть плоскости, находящая не выше прямой \(a=2t\). Аналогично область для \(t+2a\geqslant 0\) — это часть плоскости, находящаяся не ниже прямой \(a=-\frac12t\).
Тогда графиком данного уравнения \((*)\) в \(I\)-ом случае является часть параболы, входящая в данную область: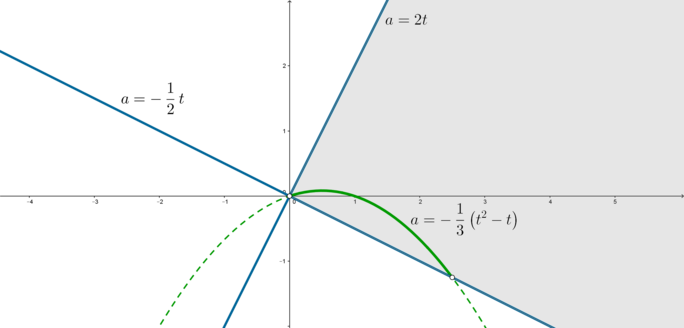
(Парабола пересекает прямую \(a=-\frac12t\) в точках \((0;0)\) и \((2,5;-1,25)\).)
II) \(2t-a<0\) и \(t+2a>0\). Парабола \(a=-t^2-3t\).
III) \(2t-a<0\) и \(t+2a<0\). Парабола \(a=\frac13\left(t^2+t\right)\).
IV) \(2t-a>0\) и \(t+2a<0\). Парабола \(a=t^2-3t\).
Аналогично рассматривая оставшиеся три случая, получим график всего уравнения \((*)\):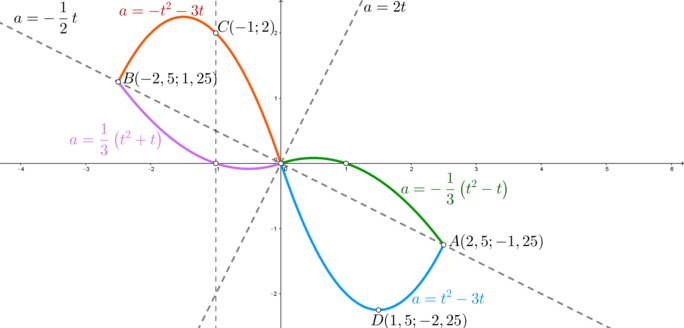
Проведем прямую \(t=-1\). Необходимо найти такие значения \(a_0\), чтобы уравнение имело хотя бы один корень \(t_0>-1\). Это значит, что прямая \(a=a_0\) должна пересечь график уравнения в хотя бы одной точке \((t_0;a_0)\) с \(t_0>-1\).
Для этого проведем прямую \(t=-1\). Тогда прямая \(a=a_0\) должна находиться ниже положения, когда она проходит через точку \(C\), и не ниже положения, когда она проходит через точку \(D\) (потому как если она будет ниже точки \(D\), то точек пересечения вообще не будет; если она будет проходить через \(C\) или выше, то не будет точек с \(t_0>-1\)). Таким образом, \(-2,25\leqslant a_0<2\).
\(a\in [-2,25;2)\)
Найдите все значения параметра \(a\), при каждом из которых уравнение \[|x-a^2-3a|+|x-a^2+2a|+|2x-a^2-a|=5a\]
имеет хотя бы один корень.
Рассмотрим две функции: \(f(x)=|x-a^2-3a|+|x-a^2+2a|+|2x-a^2-a|\) и \(g(x)=5a\).
Заметим, что \(f(x)\geqslant 0\) при всех \(x\) и \(a\) (как сумма модулей). Следовательно, для того, чтобы графики функции имели точки пересечения, нужно, чтобы \(5a\geqslant 0\), то есть \(a\geqslant 0\).
Заметим, что если третий модуль раскроется с плюсом, то, вне зависимости от того, как раскроются первые два модуля, слева будет стоять либо возрастающая функция (\(f(x)=kx+y(a)\), \(k>0\), причем \(k\) будет равно либо 4, либо 2), либо константа (когда \(k=0\)).
Если третий модуль раскроется с минусом, то, также вне зависимости от того, как раскроются первые два модуля, слева будет убывающая функция (\(f(x)=kx+y(a)\), \(k<0\), причем \(k\) будет равно либо \(-4\), либо \(-2\)) или константа (когда \(k=0\)).
При \(x\leqslant (a^2+a):2\) третий модуль раскроется с минусом, при \(x>(a^2+a):2\) – с плюсом.
Заметим, что так как \(a\geqslant 0\), то \((a^2+a):2\geqslant
0\).
Значит, функция \(f(x)=|x-a^2-3a|+|x-a^2+2a|+|2x-a^2-a|\) будет либо константой (ее график будет параллелен оси абсцисс), либо ее график будет иметь один из трех видов:
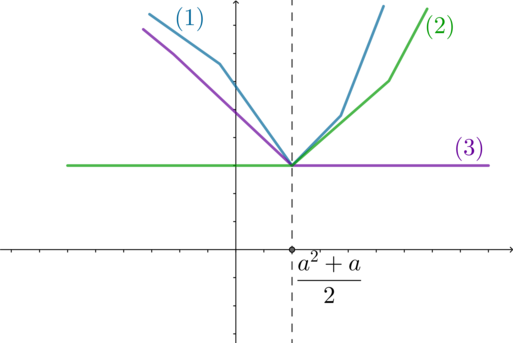
Графиком функции \(g(x)=5a\) при каждом фиксированном \(a\) будет прямая, параллельная оси абсцисс. Следовательно, для того, чтобы графики \(f\) и \(g\) имели хотя бы одну точку пересечения, нужно, чтобы график \(g\) находился не ниже вершины \(\left(\frac{a^2+a}2;
f\left(\frac{a^2+a}2\right)\right)\) графика \(f\):
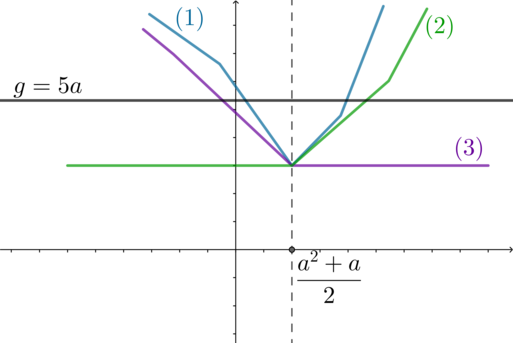
\[5a\geqslant f\left(\frac{a^2+a}2\right)\quad\Rightarrow\quad
10a\geqslant |a^2+5a|+|a^2-5a|\] Так как \(a\geqslant 0\), то \(a^2+5a\geqslant 0\), следовательно, неравенство равносильно: \[\left[\begin{gathered}\begin{aligned}
&\begin{cases} 0\leqslant a\leqslant 5\\
a^2+5a-a^2+5a\leqslant 10a\end{cases}\\[1ex]
&\begin{cases} a>5\\
a^2+5a+a^2-5a\leqslant
10a\end{cases}\end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad
0\leqslant a\leqslant 5\]
\([0;5]\)
Найдите все значения \(a\), при каждом из которых уравнение \[4\cos x-a\mathrm{tg}^2\,x=3+a\]
имеет на отрезке \([0;\pi]\) ровно один корень.
(Задача от подписчиков)
С помощью формулы \(1+\mathrm{tg}^2\,x=\dfrac1{\cos^2x}\) уравнение перепишется в виде \[4\cos x-\dfrac a{\cos^2x}-3=0\] Заметим, что если уравнение относительно \(x\) имеет ровно один корень \(x_1\) на \([0;\pi]\), то уравнение относительно \(\cos x\) имеет также ровно один корень \(t_1=\cos x_1\) на отрезке \([-1;1]\). Таким образом, рассмотрим функцию \[f(t)=4t-\dfrac a{t^2}-3\] и найдем значения \(a\), при которых график функции пересекает отрезок \([-1;1]\) оси абсцисс ровно в одной точке.
Найдем производную: \[f'(t)=4+\dfrac {2a}{t^3}\] Производная равна нулю в точке: \[t_0=-\sqrt[3]{\dfrac a2}\] Таким образом, область определения производной разбивается точками \(t_0\) и \(0\) на три промежутка, в каждом из которых она непрерывна и принимает значения одного знака.
Заметим, что при \(a>0\) \(t_0<0\), при \(a=0\) \(t_0=0\) и при \(a<0\) \(t_0>0\). В зависимости от расположения \(t_0\) относительно \(0\) у нас будут получаться разные промежутки. Поэтому рассмотрим эти три случая по отдельности.
1) \(a>0 \ \Rightarrow \ t_0<0\). Тогда знаки производной будут такими:
Заметим также, что \(f(t_0)<0\) при \(a>0\). Действительно, \[f(t_0)=\dfrac1{\sqrt[3]2}\cdot
\big(-6\cdot \sqrt[3]a-3\sqrt[3]2\big)<0\] Таким образом, график функции \(f(t)\) в этом случае выглядит схематично так:
Таким образом, левая часть графика не пересекает ось абсцисс. Следовательно, для того, чтобы функция пересекала отрезок \([-1;1]\) ровно в одной точке, нужно, чтобы правая часть графика пересекала ось абсцисс и эта точка была не правее 1. Это значит, что должно быть выполнено: \[f(1)\geqslant 0 \quad\Rightarrow\quad 4-a-3\geqslant 0
\quad\Rightarrow\quad
a\leqslant 1\] Пересекая эти значения \(a\) с условием \(a>0\), получаем ответ \(a\in (0;1]\).
2) \(a=0\). Тогда функция принимает вид \[f(t)=4t-3\] Функция пересекает ось абсцисс в точке \(t=\dfrac34\in [-1;1]\), следовательно, \(a=0\) нам подходит.
3) \(a<0 \ \Rightarrow \ t_0>0\). Тогда знаки производной будут такими:
Заметим, что в этом случае однозначно не определяется значение \(f(t_0)\). Поэтому рассмотрим по отдельности каждый случай.
3.1) \(f(t_0)<0\). Тогда \[\dfrac1{\sqrt[3]2}\cdot \big(-6\cdot \sqrt[3]a-3\sqrt[3]2\big)<0
\quad\Rightarrow \quad a>-\dfrac14.\] Таким образом, график функции \(f(t)\) в этом случае выглядит схематично так: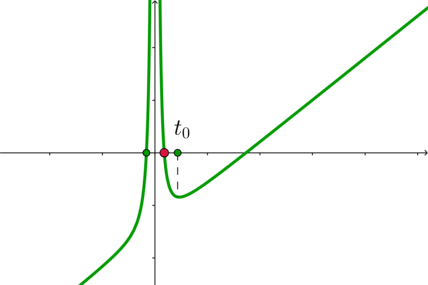
Заметим, что при \(a>-\frac14\) \[t_0=-\sqrt[3]{\dfrac a2}<\dfrac12\] Следовательно, график будет пересекать отрезок \([-1;1]\) оси абсцисс хотя бы в одной точке (красная точка). Следовательно, нам нужно, чтобы больше не было точек пересечения с \([-1;1]\). Это значит, что \[\begin{cases}
f(-1)>0\\
f(1)<0 \end{cases} \quad\Rightarrow\quad \begin{cases} -4-a-3>0\\
4-a-3<0 \end{cases} \quad\Rightarrow\quad a\in \varnothing.\] Таким образом, этот случай невозможен.
3.2) \(f(t_0)=0 \ \Rightarrow\ a=-\frac14\). График функции \(f(t)\) в этом случае выглядит схематично так: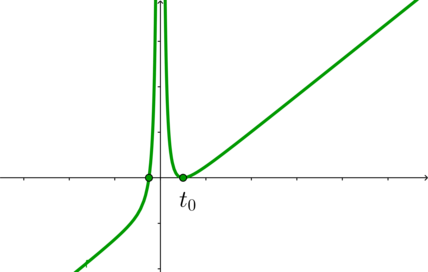
Заметим, что при \(a=-\frac14\) \[t_0=-\sqrt[3]{\dfrac a2}=\dfrac12\] Следовательно, чтобы больше не было корней на \([-1;1]\), нужно: \[f(-1)>0 \quad\Rightarrow\quad -4-a-3>0 \quad\Rightarrow\quad a<-7\] Пересекая полученные значения с \(a=-\frac14\), получаем \(a\in
\varnothing\). Таким образом, этот случай невозможен.
3.3) \(f(t_0)>0 \ \Rightarrow \ a<-\dfrac14\). График функции \(f(t)\) в этом случае выглядит схематично так: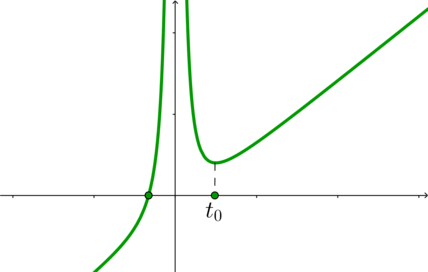
Следовательно, нужно: \[f(-1)\leqslant 0\quad\Rightarrow\quad -4-a-3\leqslant 0 \quad\Rightarrow
\quad a\geqslant -7\] Пересекая эти значения с \(a<-\frac14\), получим \(-7\leqslant a<-\frac14.\)
Теперь вспомним, что все случаи 3.1, 3.2 и 3.3 мы рассматривали при \(a<0\). Следовательно, ответ для 3 случая: \(-7\leqslant
a<-\frac14.\)
Тогда окончательный ответ в задаче: \[a\in [-7;-0,25)\cup[0;1]\]
\(a\in [-7;-0,25)\cup[0;1]\)



