Четные и нечетные функции (страница 3)
Готовиться с нами - ЛЕГКО!

\(\blacktriangleright\) Функция \(f(x)\) называется четной, если при всех \(x\) из ее области определения верно: \(f(-x)=f(x)\).
График четной функции симметричен относительно оси \(y\):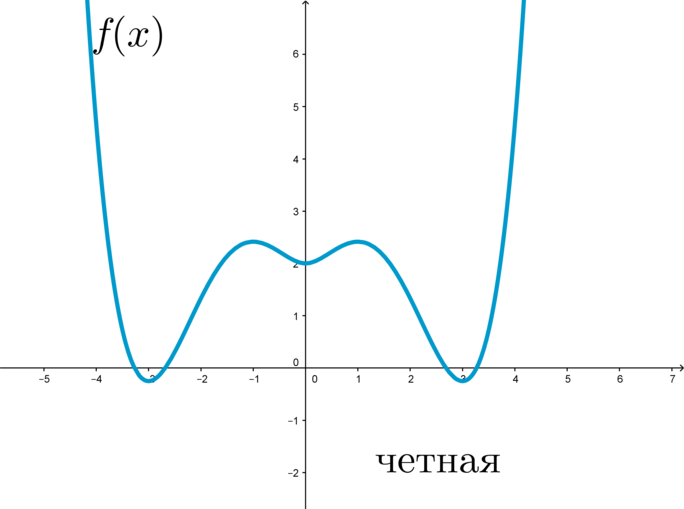
Пример: функция \(f(x)=x^2+\cos x\) является четной, т.к. \(f(-x)=(-x)^2+\cos{(-x)}=x^2+\cos x=f(x)\).
\(\blacktriangleright\) Функция \(f(x)\) называется нечетной, если при всех \(x\) из ее области определения верно: \(f(-x)=-f(x)\).
График нечетной функции симметричен относительно начала координат: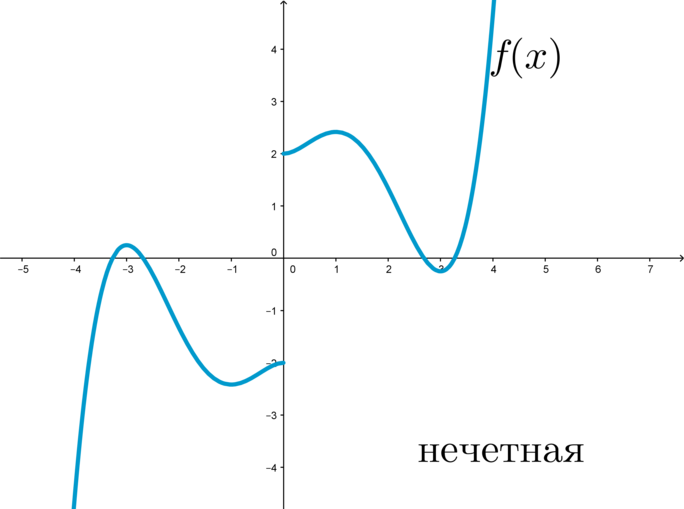
Пример: функция \(f(x)=x^3+x\) является нечетной, т.к. \(f(-x)=(-x)^3+(-x)=-x^3-x=-(x^3+x)=-f(x)\).
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
Например, функция \(f(x)=x^2-x\) является суммой четной функции \(f_1=x^2\) и нечетной \(f_2=-x\).
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
5) Если \(f(x)\) — четная функция, то уравнение \(f(x)=c \ (c\in
\mathbb{R}\)) имеет единственный корень тогда и только когда, когда \(x=0\).
6) Если \(f(x)\) — четная или нечетная функция, и уравнение \(f(x)=0\) имеет корень \(x=b\), то это уравнение обязательно будет иметь второй корень \(x=-b\).
\(\blacktriangleright\) Функция \(f(x)\) называется периодической на \(X\), если для некоторого числа \(T\ne 0\) выполнено \(f(x)=f(x+T)\), где \(x,
x+T\in X\). Наименьшее \(T\), для которого выполнено данное равенство, называется главным (основным) периодом функции.
У периодической функции любое число вида \(nT\), где \(n\in \mathbb{Z}\) также будет являться периодом.
Пример: любая тригонометрическая функция является периодической;
у функций \(f(x)=\sin x\) и \(f(x)=\cos x\) главный период равен \(2\pi\), у функций \(f(x)=\mathrm{tg}\,x\) и \(f(x)=\mathrm{ctg}\,x\) главный период равен \(\pi\).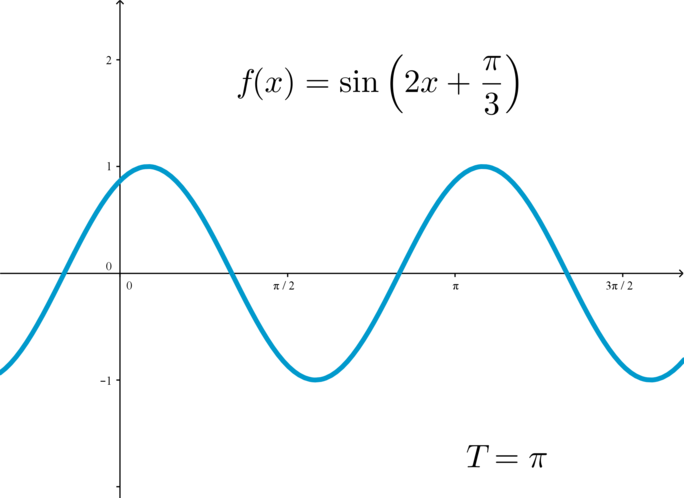
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево: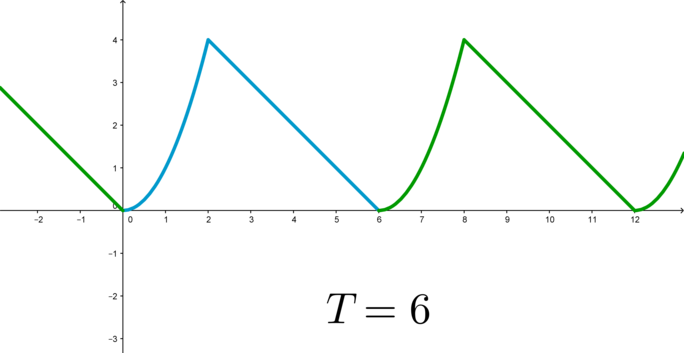
\(\blacktriangleright\) Область определения \(D(f)\) функции \(f(x)\) — это множество, состоящее из всех значений аргумента \(x\), при которых функция имеет смысл (определена).
Пример: у функции \(f(x)=\sqrt x+1\) область определения: \(x\in
[0;+\infty)\).
\(\blacktriangleright\) Область значений \(E(f)\) функции \(f(x)\) — это множество, состоящее из всех значений функции \(f(a)\), где \(a\in
D(f)\).
Пример: у функции \(f(x)=\sqrt x +1\) область значений: \(f(x)\in
[1;+\infty)\).
\(\blacktriangleright\) Уравнение \(f(x)=a\) имеет решение тогда и только тогда, когда \(a\) принадлежит области значений функции \(f(x)\), т.е. \(a\in E(f)\).
\(\blacktriangleright\) Если область значений функции \(f(x)\) не превышает некоторого числа \(A\), т.е. \(f(x)\leq A\) при всех \(x\in D(f)\), а функция \(g(x)\geq A\) при всех \(x\in D(g)\), то уравнение \[{\large{f(x)=g(x)}} \Leftrightarrow \begin{cases} f(x)=A\\g(x)=A\end{cases}\]
Найдите все значения параметра \(a\), при каждом из которых уравнение \[x^3-9x^2+108+(a^2-108a)\mathrm{tg}\,x=a\]
имеет ровно два корня.
Рассмотрим три случая: \(a=0\), \(a=108\) и \(a\ne 0;108\).
1) \(a=0\). Тогда уравнение примет вид \(x^3-9x^2=-108\). Решим его графически. Рассмотрим функцию \(y=x^3-9x^2\). Нули функции: \(x=0;9\). Производная равна \(y'=3x^2-18x\), следовательно, точки экстремума \(x=0, x=6\), причем \(x=0\) – точка максимума, \(x=6\) – точка минимума. Следовательно, график выглядит так: 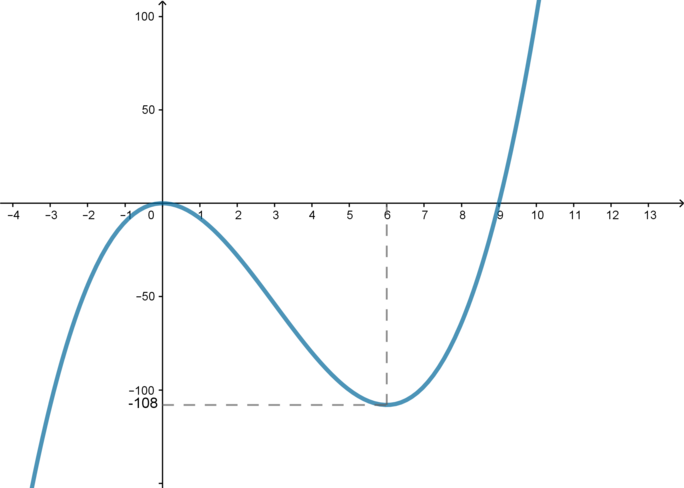
Причем \(y(6)=-108\). Следовательно, решение уравнения \(x^3-9x^2=-108\) – это абсциссы точек пересечения графиков функций \(y=x^3-9x^2\) и \(y=-108\). Таким образом, очевидно, что таких точек две.
Следовательно, \(a=0\) нам подходит.
2) \(a=108\). Тогда уравнение примет вид \(x^3-9x^2=0\). Это уравнение имеет два решения \(x=0\) и \(x=9\). Следовательно, \(a=108\) нам также подходит.
3) Пусть \(a\ne 0;108\). Рассмотрим функцию \(f(x)=(x^3-9x^2+108-a)+(a^2-108a)\mathrm{tg}\,x\). Тогда уравнение примет вид \(f(x)=0\).
Эта функция состоит из суммы двух функций: \(h(x)= x^3-9x^2+108-a\) и \(g(x)=(a^2-108a)\mathrm{tg}\,x\). Функция \(g\) определена при всех \(x\) кроме \(x=\dfrac{\pi}2+\pi k\), \(k\in\mathbb{Z}\), причем на любом отрезке \(\left[-\dfrac{\pi}2+\pi k; \dfrac{\pi}2+\pi k\right]\) принимает значения от \(-\infty\) до \(+\infty\) (вообще говоря, она еще периодическая).
Функция \(h\) кубическая, определена при любом \(x\), причем на каждом отрезке вида \(\left[-\dfrac{\pi}2+\pi k; \dfrac{\pi}2+\pi k\right]\) она ограничена (то есть ее область значений на этом отрезке – от \(h\left(-\frac{\pi}2+\pi k\right)\) до \(h\left(\frac{\pi}2+\pi
k\right)\)).
Обе функции \(g\) и \(h\) также непрерывны на любом отрезке \(\left[-\dfrac{\pi}2+\pi k; \dfrac{\pi}2+\pi k\right]\). Следовательно, функция \(f\) также непрерывна на любом таком отрезке, а также принимает значения от \(-\infty\) до \(+\infty\). Значит, на любом таком отрезке существует хотя бы одна точка, удовлетворяющая уравнению \(f(x)=c\). В частности, это верно и для \(c=0\). Следовательно, на любом отрезке вида \(\left[-\dfrac{\pi}2+\pi k;
\dfrac{\pi}2+\pi k\right]\) существует хотя бы одно решение уравнения \(f(x)=0\).
Так как таких отрезков бесконечное множество, то и решений у уравнения \(f(x)=0\) бесконечно. Следовательно, любые \(a\ne 0;108\) нам не подходят.
Таким образом, ответ \(a\in \{0;108\}\).
\(a\in \{0;108\}\)

