Динамика
Готовиться с нами - ЛЕГКО!

Два груза подвешены на достаточно длинной невесомой нерастяжимой нити, перекинутой через идеальный блок (см. рисунок). Грузы удерживали неподвижно, а затем осторожно отпустили, после чего они начали двигаться равноускоренно. Опустившись на 2 м, левый груз приобрёл скорость 4 м/с. Определите силу натяжения нити, если масса правого груза \(m = 1\) кг. Трением пренебречь. 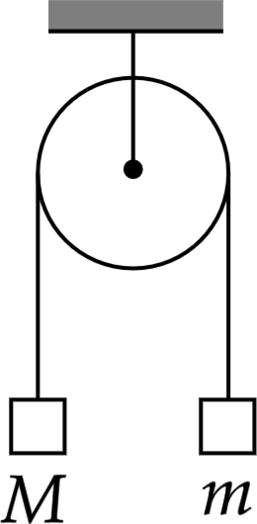
“Досрочная волна 2020 вариант 1”
Запишем закон о изменении импульса \[F =ma, \quad (1)\] где \(F\) – силы, действующие на тело, \(a\) – ускорение тела.
Запишем силы, которые действуют на тело массой \(m\), на ось, направленную ввертикально вверх \[T-mg\quad (2)\] А расстояние можно найти по формуле: \[S=\dfrac{v^2}{2a} \Rightarrow a=\dfrac{v^2}{2S}, \quad (3)\] где \(v\) – скорость тела.
Откуда сила натяжения нити \[T=\dfrac{m v^2}{2S}+mg=\dfrac{1\text{ кг}\cdot 16\text{ м$^2$/с$^2$}}{2\cdot 2\text{ м}}+ 1\text{ кг}\cdot 10\text{ Н/кг}=14\text{ Н}\]
Груз массой 1 кг, находящийся на столе, связан лёгкой нерастяжимой нитью, переброшенной через идеальный блок, с другим грузом. На первый груз действует горизонтальная постоянная сила , \(\vec{F}\) равная по модулю 10 Н (см. рисунок). Второй груз движется из состояния покоя с ускорением 2 м/с\(^2\), направленным вверх. Коэффициент трения скольжения первого груза по поверхности стола равен 0,2. Чему равна масса второго груза?

“Демоверсия 2019”
Так как бруски связаны нерастяжимой нитью, то они будут двигаться с одинаковым ускорением, которое будет создаваться силой \(F\), которой препятствуют сила тяжести второго бруска \(m_2g\) и сила трения первого бруска \(F_\text{тр}=\mu m_1g\) Тогда второй закон Ньютона можно записать в виде \[m_1a+m_2a=F-m_2g-\mu m_1g\] Отсюда масса второго груза \[m_2=\dfrac{F-m_1(\mu g+a)}{a+g}=\dfrac{10\text{ Н}-1\text{ кг}(0,2 \cdot 10\text{ Н/кг}+2\text{ Н/кг})}{10\text{ Н/кг}+2\text{ Н/кг}}=0,5\text{ кг}\]
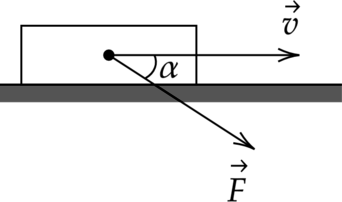
Брусок массой 2 кг движется по горизонтальному столу. На тело действует сила \(\vec{F}\) под углом \(\alpha\) = 30\(^\circ\) к горизонту (см. рисунок). Коэффициент трения между бруском и столом равен 0,3. Каков модуль силы \(\vec{F}\) , если модуль силы трения, действующей на тело, равен 7,5 Н?
“Демоверсия 2020”
Запишем второй закон Ньютона на вертикальную ось \[N=mg+F\sin \alpha\] сила трения же равна: \[F_\text{ тр}= \mu N\] \[F_\text{ тр}= \mu(mg+F\sin \alpha)\] Откуда сила \(F\) \[F=\dfrac{F_\text{ тр}-\mu m g}{\mu \sin \alpha}=\dfrac{7,5\text{ Н}-0,3\cdot 2\text{ кг}\cdot 10\text{ Н/кг}}{0,3\cdot \sin 30^{\circ}}=10\text{ Н}\]
Груз массой 1 кг, находящийся на столе, связан лёгкой нерастяжимой нитью, переброшенной через идеальный блок, с другим грузом. На первый груз действует горизонтальная постоянная сила , \(\vec{F}\) равная по модулю 10 Н (см. рисунок). Второй груз движется из состояния покоя с ускорением 2 м/с\(^2\), направленным вверх. Коэффициент трения скольжения первого груза по поверхности стола равен 0,2. Чему равна масса второго груза?

“Демоверсия 2019”
Так как бруски связаны нерастяжимой нитью, то они будут двигаться с одинаковым ускорением, которое будет создаваться силой \(F\), которой препятствуют сила тяжести второго бруска \(m_2g\) и сила трения первого бруска \(F_\text{тр}=\mu m_1g\) Тогда второй закон Ньютона можно записать в виде \[m_1a+m_2a=F-m_2g-\mu m_1g\] Отсюда масса второго груза \[m_2=\dfrac{F-m_1(\mu g+a)}{a+g}=\dfrac{10\text{ Н}-1\text{ кг}(0,2 \cdot 10\text{ Н/кг}+2\text{ Н/кг})}{10\text{ Н/кг}+2\text{ Н/кг}}=0,5\text{ кг}\]
Груз массой \(m=20\) кг можно поднимать с помощью системы из подвижного и неподвижного блоков. С какой постоянной силой F надо тянуть верёвку, чтобы за время подъёма \(t\)=0,5 с груз из состояния покоя достиг скорости \(v\)=2 м/с? Массами верёвки, блоков и трением в осях пренебречь, ответ дайте в Ньютонах.
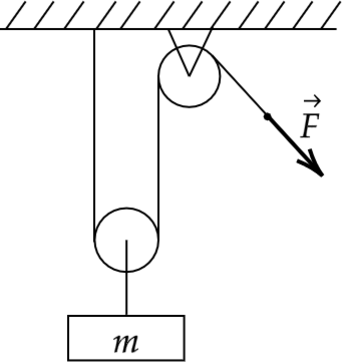
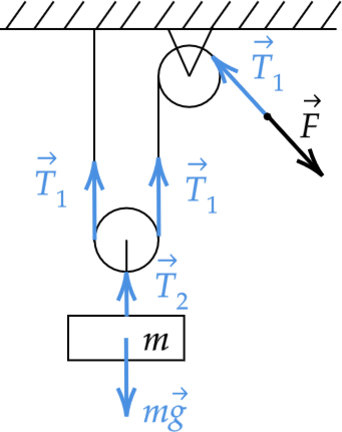
Из рисунка видно, что \(T_1=F\). На подвижный блок действуют две силы \(T_1\) вверх и одна \(T_2\) вниз, следовательно , так как блок невесомый, то \(T_2=2T_1\). Второй закон Ньютона для груза: \[\vec{T_2}+m\vec{g}=m\vec{a}\] Спроецируем на ось, направленную вертикально вверх: \[OY: \quad T_2-mg=ma\] Ускорение найдем из кинематики: \[a_y=\frac{\upsilon_{y1}-\upsilon_{y0}}{\Delta t} \quad \Rightarrow \quad a=\frac{\upsilon}{\Delta t}\] Объединяя все уравнения, мы получим: \[T_2=mg+ma\quad \Rightarrow \quad 2T_1=mg+ma \quad \Rightarrow \quad F=\frac{mg+ma}{2}=\frac{mg+m\cfrac{\upsilon}{\Delta t}}{2}\] \[F=\frac{200\text{ Н}+20\text{ кг}\cfrac{2\text{ м/с}}{0,5\text{ с}}}{2}=140 \text{ Н}\]
Брусок массой \(m=0,6\) кг движется поступательно по горизонтальной плоскости под действием силы \(F=6\) Н, направленной под углом \(\alpha=30^\circ\) к горизонту. Найдите силу трения, если коэффициент трения равен \(\mu=0,2\). Ответ дайте в Ньютонах.
Запишем второй закон Ньютона: \[\vec{F}+\vec{N}+\vec{F_\text{тяж}}=m\vec{a},\] где \(N\) – сила реакции опоры, \(F_\text{тяж}\) – сила тяжести, \(a\) – ускорение бруска.
Так как брусок движется по горизонтальной плоскости, то у него нет вертикального ускорения, значит, второй закон Ньютона можно переписать с учетом проекций в виде \[F \sin \alpha +N -mg=0 \Rightarrow N=mg-F\sin \alpha \quad (1)\] Сила трения равна: \[F_\text{тр}=\mu N\quad (2)\] Подставим (1) в (2) \[F_\text{тр}=\mu(mg-F\sin\alpha)=0,2(6\text{ Н}-6\text{ Н}\cdot 0,5)=0,6\text{ Н}\]
Коэффициент трения колес автомобиля о землю равен \(\mu=0,4\). Найдите наименьший радиус поворота, чтобы водитель смог избежать аварии при скорости \(v=10\) м/с. Ответ приведите в метрах.
При движении на повороте радиусом \(R\) будет создаваться центростремительное ускорение \[a=\dfrac{v^2}{R}\] Кроме того, по второму закону Ньютона \[\vec{F_\text{тяж}}+\vec{F_\text{тр}}+ \vec{N}=ma\] Спроецируем на ось, сонаправленную с движением автомобиля, с учетом того, что в нашем случае \(F_\text{тяж}=N\), а сила трения равна \(F_\text{тр}=\mu N\) \[ma=\mu N \Rightarrow m \dfrac{v^2}{R}=\mu m g \Rightarrow R= \dfrac{v^2}{\mu g}=\dfrac{100\text{ м$^2$/с$^2$}}{0,4 \cdot 10\text{ м/с$^2$}}=25\text{ м}\]



