Динамика (страница 2)
Готовиться с нами - ЛЕГКО!

Одинаковые бруски, связанные нитью, движутся под действием внешней силы \(F\) по гладкой горизонтальной поверхности (см. рисунок). Найдите, во сколько раз увеличится сила натяжения нити между брусками, если третий брусок переложить с первого на второй.

Поскольку бруски связаны нерастяжимой нитью, они двигаются с одинаковым ускорением. Обозначим \(T\) силу натяжения нити. Тогда для второго бруска второй закон Ньютона \[T=ma\] Для первого и третьего \[F-T=2ma\] Объединяя оба случая получаем \[F-T=2T \Rightarrow T=\dfrac{F}{3}\] Когда переложим третий брусок на второй, то для третьего и второго второй закон Ньютона будет выглядеть следующим образом \[T'=2ma\] А для первого \[F-T'=ma\] Объединяя оба случая \[F-T'=\dfrac{T'}{2} \Rightarrow T'=\dfrac{2F}{3}\] Отсюда следует, что сила натяжения нити увеличится в 2 раза.
Одинаковые бруски, связанные нитью, движутся под действием внешней силы \(F\) по гладкой горизонтальной поверхности (см. рисунок). Найдите, во сколько раз увеличится сила натяжения нити между брусками, если на второй брусок добавить брусок той же массы. Ответ округлите до десятых.

Поскольку бруски связаны нерастяжимой нитью, они двигаются с одинаковым ускорением. Обозначим \(T\) силу натяжения нити. Тогда для второго бруска второй закон Ньютона \[T=ma\] Для первого \[F-T=ma\] Объединяя оба случая получаем \[F-T=T \Rightarrow T=\dfrac{F}{2}\] Когда добавим на второй брусок еще один такой же, то для третьего и второго второй закон Ньютона будет выглядеть следующим образом \[T'=2ma\] А для первого \[F-T'=ma\] Объединяя оба случая \[F-T'=\dfrac{T'}{2} \Rightarrow T'=\dfrac{2F}{3}\] Отсюда отношение сил натяжения нитей \[\dfrac{T'}{T}=\dfrac{\dfrac{2F}{3}}{\dfrac{F}{2}}=\dfrac{4}{3}\]
Одинаковые бруски, связанные нитью, движутся под действием внешней силы \(F\) по гладкой горизонтальной поверхности (см. рисунок). Найдите, во сколько раз уменьшится ускорение системы, если на второй брусок положить брусок такой же массой.

Поскольку бруски связаны нерастяжимой нитью, они двигаются с одинаковым ускорением. Обозначим \(T\) силу натяжения нити. Тогда для второго бруска второй закон Ньютона \[T=ma\] Для первого \[F-T=ma\] Объединяя оба случая получаем \[F-ma=ma \Rightarrow a=\dfrac{F}{2m}\] Когда добавим на второй брусок еще один такой же, то для третьего и второго второй закон Ньютона будет выглядеть следующим образом \[T'=2ma'\] А для первого \[F-T'=ma'\] Объединяя оба случая \[F-2ma'=ma' \Rightarrow a'=\dfrac{F}{3m}\] Отсюда отношение ускорений \[\dfrac{a'}{a}=\dfrac{\dfrac{F}{3m}}{\dfrac{F}{2m}}=\dfrac{2}{3}\] Значит, ускорение уменьшится в 1,5 раза.
По гладкому горизонтальному столу из состояния покоя движется массивный брусок, соединенный с грузом массой \(m=0,2\) кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Ускорение груза равно \(a=4\) м/с\(^2\) Чему равна масса бруска? Ответ укажите в килограммах. 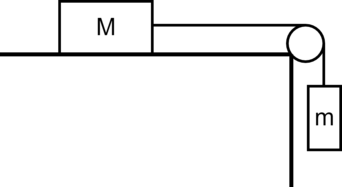
Поскольку грузы связаны нерастяжимой нитью, они двигаются с одинаковыми ускорениями. Невесомость нити означает, что сила натяжения нити постоянна по всей длине, на оба груза нить действует с одинаковой по величине силой \(T\). Запишем второй закон Ньютона для груза и бруска. Для груза: \[mg-T=ma\] Для бруска \[T=Ma\] Сложим оба уравнения и получим \[mg=Ma+ma\] Отсюда масса бруска \[M=\dfrac{m(g-a)}{a}=\dfrac{0,2\text{ кг}(10\text{ м/с$^2$}-4\text{ м/с$^2$})}{4\text{ м/с$^2$}}=0,3 \text{ кг}\]
Брусок массой \(M=3\) кг соединен с бруском массой \(m=2\) кг с помощью невесомой и нерастяжимой нитью, перекинутой через блок. Найдите, с каким ускорением будет двигаться брусок массой \(m\)?

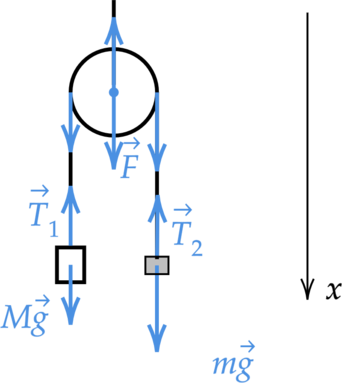 Обозначим все силы, действующие на бруски Запишем второй закон Ньютона для брусков на ось \(x\). \[\begin{cases}
M: & Ma=Mg-T\\
m: & -am=mg-T\\
\end{cases}\] Вычтем из первого уравнения второе и получим \[Ma+ma=Mg-mg\] Выразим ускорение \[a=\dfrac{Mg-mg}{m+M}=\dfrac{3\text{ кг}\cdot 10\text{ Н/кг}-2\text{ кг}\cdot 10\text{ Н/кг}}{2\text{ кг}+3\text{ кг}}=2\text{ м/с$^2$}\]
Обозначим все силы, действующие на бруски Запишем второй закон Ньютона для брусков на ось \(x\). \[\begin{cases}
M: & Ma=Mg-T\\
m: & -am=mg-T\\
\end{cases}\] Вычтем из первого уравнения второе и получим \[Ma+ma=Mg-mg\] Выразим ускорение \[a=\dfrac{Mg-mg}{m+M}=\dfrac{3\text{ кг}\cdot 10\text{ Н/кг}-2\text{ кг}\cdot 10\text{ Н/кг}}{2\text{ кг}+3\text{ кг}}=2\text{ м/с$^2$}\]
Чему равен модуль силы \(F\), с которой двигают брусок массой \(m=2 \) кг, при этом коэффициент трения равен \(\mu\)=0,2, а сила \(F\) направлена под углом \(\alpha=30^\circ\) к горизонту (см. рисунок). Модуль силы трения, действующей на брусок, \(F_\text{тр}\) = 2,8 Н.

Сила трения равна \[F_\text{тр}=\mu N, \quad (1)\] где \(N\) – сила реакции опоры.
Запишем второй закон Ньютона на вертикальную ось. \[N-mg+F\sin 30^\circ=0 \Rightarrow N=mg-F\sin 30^\circ \quad (2)\] Подставим (2) в (1) и выразим силу \(F\) \[F=\dfrac{\mu mg - F_\text{тр}}{\mu \sin \alpha}=\dfrac{0,2 \cdot 20\text{ Н}-2,8\text{ Н}}{0,2 \cdot 0,5}=12\text{ Н}\]
Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы \(F\) приложенной к грузу \(M_1\) = 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити \(T=4\) Н, при этом модуль силы \(F\) равен 12 Н. Чему равна масса второго груза \(M_2\)?

Запишем второй закон Ньютона для каждого из тел \[\begin{cases}
F-T=M_1a\\
T=M_2a\\
\end{cases}\] Сложим два уравнения и получим \[F=(M_1+M_2)a \Rightarrow a=\dfrac{F}{M_1+M_2}\] Из второго уравнения системы \[T=aM_2=\dfrac{F}{M_1+M_2} M_2 \Rightarrow M_2=\dfrac{T}{F-T}M_1=\dfrac{4\text{ Н}}{12\text{ Н}-4\text{Н}}2\text{ кг}=1\text{ кг}\]



