Электростатика
Готовиться с нами - ЛЕГКО!

Точечные заряды закреплены так, как показано на рисунке. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости электростатического поля в точке \(O\)? Ответ запишите словом (словами). 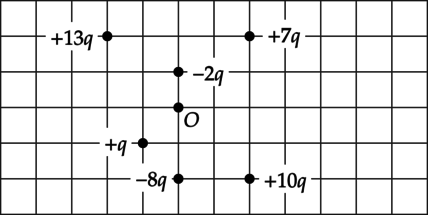
По принципу суперпозиции, напряженность поля в точке \(O\) есть сумма напряженностей полей, создаваемых всеми зарядами по отдельности: \[\vec{E_{\text{общ}}}=\vec{E_1}+\vec{E_2}+\dots+\vec{E_n}\] Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом — от заряда. Поле точечного заряда пропорционально величине заряда и ослабевает с расстоянием. Это выражается зависимостью: \[E=\dfrac{Q}{r^2}\] 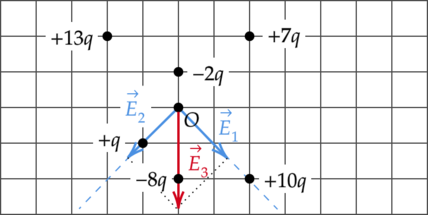
Напряженность поля, создаваемого зарядами \(+13q\) и \(+10q\), направлена в сторону заряда \(+10q\) и по модулю равна: \[E_1=\dfrac{3q}{(2q)^2}\] Напряженности полей зарядов \(+7q\) и \(+q\) в точке \(O\): \[E_{+7q}=\dfrac{7q}{(2r)^2}\; \; \; \; \; \; \; \; \; \; \; \; \; \; E_{+q}=\dfrac{q}{r^2}\] Тогда результирующая напряженность полей этих зарядов будет равна: \[E_2=\dfrac{7q}{(2r)^2}-\dfrac{q}{r^2}=\dfrac{3q}{(2r)^2} \; \; \; \Rightarrow \; \; \; E_1=E_2\] Аналогично с результирующей напряженностью полей зарядов \(-2q\) и \(-8q\): \[E_4=\dfrac{(-8q)}{(2r)^2}-\frac{(-2q)}{r^2}=0\] Таким образом, результирующий вектор \(\vec{E_3}\) напряженности электрического поля в точке \(O\) направлен вниз.
Точечные заряды закреплены так, как показано на рисунке. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости электростатического поля в точке \(O\)? Ответ запишите словом (словами).

Разобьем заряды на пары так, чтобы соединяющая их прямая проходила через точку \(O\): 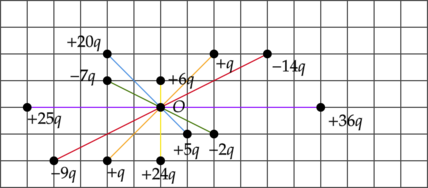
По принципу суперпозиции, напряженность поля в точке \(O\) есть сумма напряженностей полей, создаваемых всеми зарядами по отдельности: \[\vec{E_{\text{общ}}}=\vec{E_1}+\vec{E_2}+\dots+\vec{E_n}\] Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом — от заряда. Поле точечного заряда пропорционально величине заряда \(Q\) и ослабевает с расстоянием \(r\). Это выражается зависимостью: \[E=\dfrac{Q}{r^2}\] 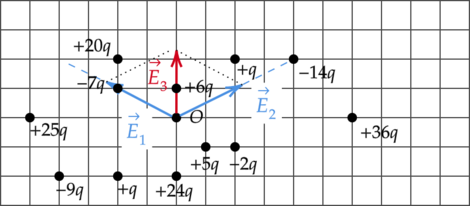
Так как напряженность поля зарядов \(+20q\) и \(+5q\) в точке \(O\) равна: \[E_{+q}=\dfrac{20q}{(2r_1)^2}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; E_{+5q}=\dfrac{5q}{r_1^2}\] Тогда результирующая напряженность полей этих зарядов будет равна нулю: \[\dfrac{20q}{(2r_1)^2}-\dfrac{5q}{r_1^2}=0\] Аналогично с результирующей напряженностью полей зарядов \(+25q\) и \(+36q\): \[\dfrac{25q}{(5r_2)^2}-\dfrac{36q}{(6r_2)^2}=0\] Напряженность поля, создаваемого зарядами \(+24q\) и \(+6q\): \[\dfrac{24q}{(2r_2)^2}-\dfrac{6q}{r_2^2}=0\] Поле зарядов \(+q\) и \(+q\) тоже равно 0. Напряженность поля, создаваемого зарядами \(-7q\) и \(-2q\), направлена в сторону заряда \(-7q\) и по модулю равна: \[E_1=\dfrac{5q}{(r_3)^2}\] А напряженность поля, создаваемого зарядами \(-14q\) и \(-9q\), равна: \[E_2=\dfrac{5q}{(r_3)^2}\] Отсюда следует, что: \[E_1=E_2\] Таким образом, результирующий вектор \(\vec{E_3}\) напряженности электрического поля в точке \(O\) направлен вверх.
Три точечных заряда закреплены на плоскости так, как показано на рисунке. Куда направлена относительно рисунка (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) кулоновская сила \(F\), действующая на отрицательный точечный заряд \(Q\)? Ответ запишите словом (словами).

Согласно закону Кулона, сила взаимодействия электрических зарядов прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними: \[F=k\dfrac{|q_1||q_2|}{r^2}\] 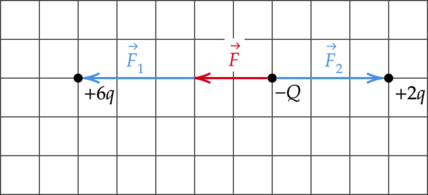
Сила взаимодействия между зарядами \(+6q\) и \(-Q\) направлена в сторону \(+6q\) (разноименные заряды притягиваются) и по модулю равна: \[F_1=k\dfrac{6qQ}{(5r)^2}\] А между зарядами \(+2q\) и \(-Q\) сила взаимодействия направлена в сторону \(+2q\) и равна: \[F_2=k\dfrac{2qQ}{(3r)^2}\] Заметим, что \[k\dfrac{6qQ}{(5r)^2}>k\dfrac{2qQ}{(3r)^2} \; \; \; \Rightarrow \; \; \; F_1>F_2\] Таким образом, результирующий вектор кулоновской силы \(F\) сонаправлен с вектором \(F_1\) и направлен влево.
Пять точечных зарядов закреплены на плоскости так, как показано на рисунке. Куда направлена относительно рисунка (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) кулоновская сила \(F\), действующая на отрицательный точечный заряд \(-Q\)? Ответ запишите словом (словами).
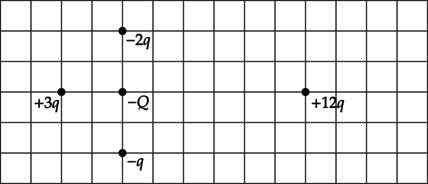
Согласно закону Кулона, сила взаимодействия электрических зарядов прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними: \[F=k\dfrac{|q_1||q_2|}{r^2}\] где \(k\) — электрическая постоянная.
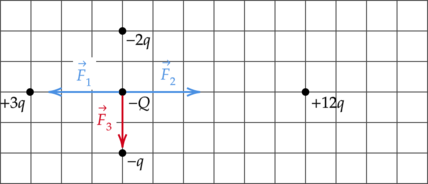
Сила взаимодействия между зарядами \(+3q\) и \(-Q\) направлена в сторону \(+3q\) (разноименные заряды притягиваются) и по модулю равна: \[F_1=k\dfrac{3qQ}{(3r)^2}=k\dfrac{qQ}{3r^2}\] А между зарядами \(+12q\) и \(-Q\) направлена в сторону \(+12q\) и равна: \[F_2=k\dfrac{12qQ}{(6r)^2}=k\dfrac{qQ}{3r^2}\] Заметим, что \(F_1=F_2\). Тогда равнодействующая этих сил равна 0.
Модуль заряда \(|-2q|>|-q|\). Таким образом, результирующий вектор кулоновской силы \(F\) направлен в сторону \(-q\) (заряды одного знака притягиваются), то есть вниз.
Отрицательный заряд \(–q\) находится в поле двух неподвижных зарядов: положительного \(+Q\) и отрицательного \(–Q\) (см. рисунок). Куда направлено относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) ускорение заряда \(–q\) в этот момент времени, если на него действуют только заряды \(+Q\) и \(–Q\)? Ответ запишите словом (словами).
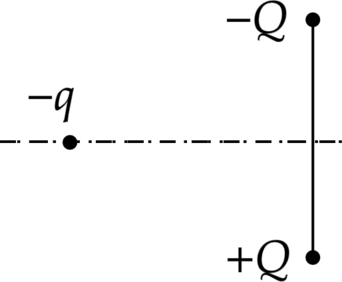
“Демоверсия 2018”
Отрицательный заряд будет отталкивать, а положительный притягивать, при чем силы притяжения будут равны, следовательно, горизонтальные проекции сил уничтожат друг друга, а вертикальные сложатся и будут направлены вниз.
Положительный точечный заряд \(+q\) находится в поле двух неподвижных точечных зарядов: положительного \(+Q\) и отрицательного \(–Q\) (см. рисунок). Куда направлено относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) ускорение заряда \(+q\) в этот момент времени, если на него действуют только заряды \(+Q\) и \(–Q\)? Ответ запишите словом (словами).
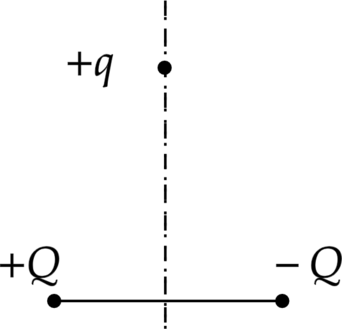
“Демоверсия 2020”
Отрицательный заряд будет отталкивать, а положительный притягивать, при чем силы притяжения будут равны, следовательно, вертикальные проекции сил уничтожат друг друга, а горизнотальные сложатся и будут направлены вправо.
Куда направлена относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) кулоновская сила \(\vec{F}\) действующая на отрицательный точечный заряд \(- q\), помещённый в центр квадрата, в углах которого находятся заряды: \(+q, +q, -q, -q\) (см. рисунок)? Ответ запишите словом (словами)

“Демоверсия 2021”
Положительные заряды притягивают, а отрицательные заряды отталкивают, силы суммируются и направлены вправо



