Электростатика (страница 2)

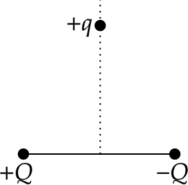
Заряды, имеющие одинаковые знаки, отталкиваются, а заряды, имеющие разные знаки — притягиваются. Исходя из этого, изобразми силы, действующие на заряд \(+q\) со стороны зарядов \(+Q\) и \(-Q\):

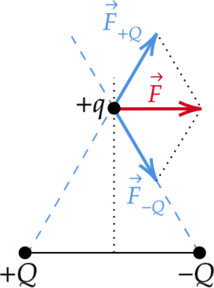
Равнодействующая сил, которые действуют на заряд \(+q\) направлена вправо. Так как вектор ускорения заряда сонаправлен с направлением вектора равнодействующей силы \(\vec{F}\), то он также направлен вправо.

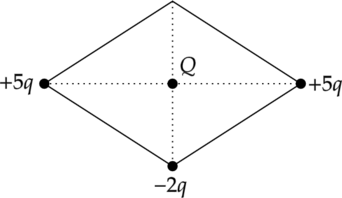
Заряды, имеющие одинаковые знаки, отталкиваются, а заряды, имеющие разные знаки — притягиваются. Исходя из этого, изобразми силы, действующие на заряд \(Q\) со стороны зарядов \(+5q\) , \(+5q\) и \(-2q\):

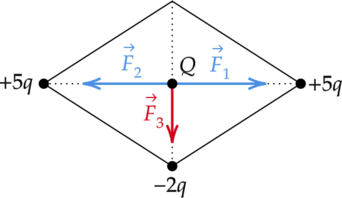
Равнодействующая кулоновских сил \(\vec{F_1}\) и \(\vec{F_2}\), действующих на заряд \(Q\) равна 0, так как левый и правый заряды равны по знаку и по модулю.
Тогда остаётся сила \(\vec{F_3}\), которая направлена вниз, потому что \(Q\) и \(-2q\) противоположны по знаку, следовательно, притягиваются. Таким образом, вектор кулоновской силы \( \vec{F}\) направлен вниз.

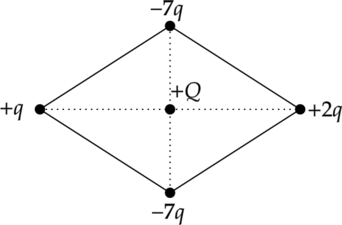
Равнодействующая кулоновских сил \(\vec{F_3}\) и \(\vec{F_4}\), действующих на заряд \(Q\), равна 0, так как верхний и нижний заряды равны по знаку и по модулю. Сила \(\vec{F_1}\) направлена вправо, так как \(Q\) и \(q\) положительны, тогда \(\vec{F_2}\) — влево (одинаковые по знаку заряды отталкиваются).

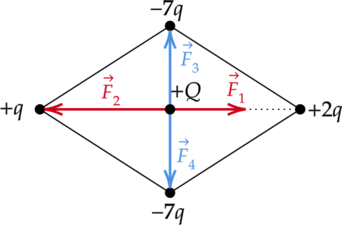
Но \(2q > q\), тогда \(|\vec{F_2}| >| \vec{F_1}|\) и равнодействующая этих сил сонаправлена с вектором \(\vec{F_2}\), то есть вектор кулоновской силы \(F\) направлен влево.

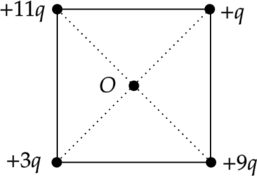
По прин­ци­пу су­пер­по­зи­ции, на­пря­жен­ность поля в точке \(O\) есть сумма на­пря­жен­но­стей полей, со­зда­ва­е­мых всеми за­ря­да­ми по от­дель­но­сти: \[\vec{E_{\text{общ}}}=\vec{E_1}+\vec{E_2}+\dots+\vec{E_n}\] Поле от­ри­ца­тель­но­го то­чеч­но­го за­ря­да на­прав­ле­но к за­ря­ду, а поле, со­зда­ва­е­мое по­ло­жи­тель­ным за­ря­дом — от за­ря­да. Поле то­чеч­но­го за­ря­да про­пор­ци­о­наль­но ве­ли­чи­не за­ря­да \(Q\) и осла­бе­ва­ет с рас­сто­я­ни­ем \(r\). Это выражается зависимостью: \[E=\dfrac{Q}{r^2}\]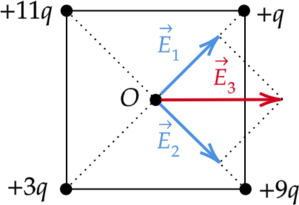
На­пря­жен­ность поля со­зда­ва­е­мо­го за­ря­да­ми \(q\) и \(3q\) на­прав­ле­но в сто­ро­ну за­ря­да \(q\) и по мо­ду­лю равна: \[|E_1|=\dfrac{2q}{r^2}\] На­пря­жен­ность поля со­зда­ва­е­мо­го за­ря­да­ми \(11q\) и \(9q\) на­прав­ле­но в сто­ро­ну за­ря­да \(9q\) и по мо­ду­лю равна: \[|E_2|=\dfrac{2q}{r^2}\] Таким об­ра­зом, век­тор \(\vec{E_3}\) на­пря­жен­но­сти элек­три­че­ско­го поля в цен­тре \(O\) квадрата на­прав­лен вправо.

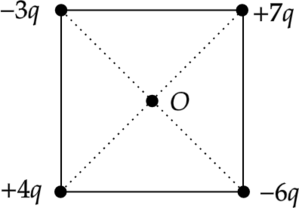
По прин­ци­пу су­пер­по­зи­ции, на­пря­жен­ность поля в точке \(O\) есть сумма на­пря­жен­но­стей полей, со­зда­ва­е­мых всеми за­ря­да­ми по от­дель­но­сти: \[\vec{E_{\text{общ}}}=\vec{E_1}+\vec{E_2}+\dots+\vec{E_n}\] Поле от­ри­ца­тель­но­го то­чеч­но­го за­ря­да на­прав­ле­но к за­ря­ду, а поле, со­зда­ва­е­мое по­ло­жи­тель­ным за­ря­дом — от за­ря­да. Поле то­чеч­но­го за­ря­да про­пор­ци­о­наль­но ве­ли­чи­не за­ря­да \(Q\) и осла­бе­ва­ет с рас­сто­я­ни­ем \(r\). Это выражается зависимостью: \[E=\dfrac{Q}{r^2}\]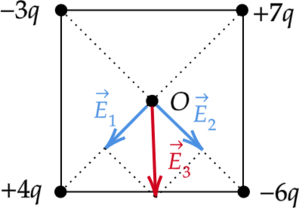
На­пря­жен­ность поля со­зда­ва­е­мо­го за­ря­да­ми \(+4q\) и \(+7q\) на­прав­ле­но в сто­ро­ну за­ря­да \(+4q\) и по мо­ду­лю равна: \[E_1=\dfrac{3q}{r^2}\] На­пря­жен­ность поля со­зда­ва­е­мо­го за­ря­да­ми \(-3q\) и \(-6q\) на­прав­ле­но в сто­ро­ну за­ря­да \(-6q\) и по мо­ду­лю равна: \[E_2=\dfrac{3q}{r^2}\] Таким об­ра­зом, век­тор \(\vec{E_3}\) на­пря­жен­но­сти элек­три­че­ско­го поля в цен­тре \(O\) квадрата на­прав­лен вниз.

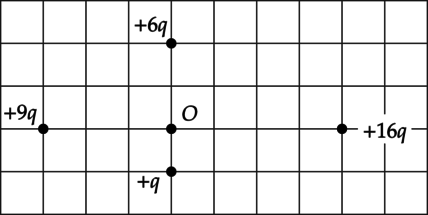
По прин­ци­пу су­пер­по­зи­ции, на­пря­жен­ность поля в точке \(O\) есть сумма на­пря­жен­но­стей полей, со­зда­ва­е­мых всеми за­ря­да­ми по от­дель­но­сти: \[\vec{E_{\text{общ}}}=\vec{E_1}+\vec{E_2}+\dots+\vec{E_n}\] Поле от­ри­ца­тель­но­го то­чеч­но­го за­ря­да на­прав­ле­но к за­ря­ду, а поле, со­зда­ва­е­мое по­ло­жи­тель­ным за­ря­дом — от за­ря­да. Поле то­чеч­но­го за­ря­да про­пор­ци­о­наль­но ве­ли­чи­не за­ря­да \(Q\) и осла­бе­ва­ет с рас­сто­я­ни­ем \(r\). Это выражается зависимостью: \[E=\dfrac{Q}{r^2}\]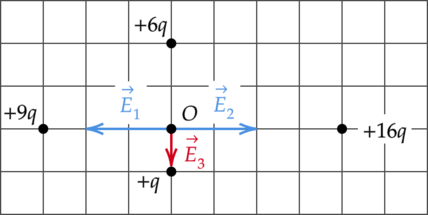
Так как напряженность поля заряда \(+3q\) в точке \(O\): \[E_1=\dfrac{9q}{(3r)^2}=\dfrac{q}{r^2}\] А напряженность поля заряда \(+16q\) в точке \(O\): \[E_2=\dfrac{16q}{(4r)^2}=\dfrac{q}{r^2} \; \; \; \Rightarrow \; \; \; E_1=E_2\] Тогда ре­зуль­ти­ру­ю­щая напряженность полей этих зарядов будет равна 0. Поле заряда \(+6q\) больше поля заряда \(+q\), так как: \[\dfrac{6q}{(2r)^2}>\dfrac{q}{r^2}\] Таким об­ра­зом, результирующий век­тор \(\vec{E_3}\) на­пря­жен­но­сти элек­три­че­ско­го поля в точке \(O\) направлен в сторону \(+q\), то есть вниз.

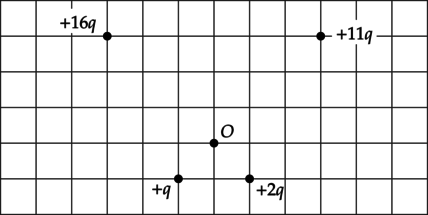
По прин­ци­пу су­пер­по­зи­ции, на­пря­жен­ность поля в точке \(O\) есть сумма на­пря­жен­но­стей полей, со­зда­ва­е­мых всеми за­ря­да­ми по от­дель­но­сти: \[\vec{E_{\text{общ}}}=\vec{E_1}+\vec{E_2}+\dots+\vec{E_n}\] Поле от­ри­ца­тель­но­го то­чеч­но­го за­ря­да на­прав­ле­но к за­ря­ду, а поле, со­зда­ва­е­мое по­ло­жи­тель­ным за­ря­дом — от за­ря­да. Поле то­чеч­но­го за­ря­да про­пор­ци­о­наль­но ве­ли­чи­не за­ря­да \(Q\) и осла­бе­ва­ет с рас­сто­я­ни­ем \(r\). Это выражается зависимостью: \[E=\dfrac{Q}{r^2}\]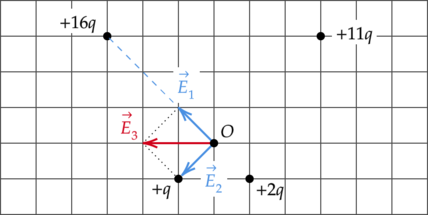
Так как напряженность поля заряда \(+2q\) в точке \(O\) равна: \[E_{+q}=\dfrac{2q}{r^2}\] А напряженность поля заряда \(+16q\) в точке \(O\): \[E_{+16q}=\dfrac{16q}{(3r)^2}\] Тогда ре­зуль­ти­ру­ю­щая напряженность полей этих зарядов будет равна: \[E_1=\dfrac{2q}{r^2}-\dfrac{16q}{(3r)^2}=\dfrac{2q}{(3r)^2}\] Аналогично с результирующим полем зарядов \(+11q\) и \(+q\): \[E_2=\dfrac{11q}{(3r)^2}-\dfrac{q}{r^2}=\dfrac{2q}{(3r)^2} \; \; \; \Rightarrow \; \; \; E_1=E_2\] Таким об­ра­зом, результирующий век­тор \(\vec{E_3}\) на­пря­жен­но­сти элек­три­че­ско­го поля в точке \(O\) направлен влево.