Магнитное поле. ЭДС индукции (страница 2)
Готовиться с нами - ЛЕГКО!

Кольцо из проволоки находится в однородном магнитном поле. Модуль индукции магнитного поля уменьшают с постоянной скоростью. Затем кольцо заменяют на другое с площадью в два раза больше, оставляя расположение относительно линий магнитной индукции тем же, при этом скорость изменения модуля индукции магнитного поля уменьшают в 4 раза. Как в результате этого изменятся следующие физические величины: ЭДС индукции, возникающая в кольце и cкорость изменения потока через кольцо .
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
\[\begin{array}{|c|c|}
\hline
\text{ ЭДС индукции,}&\text{ Скорость изменения магнитного }\\
\text{ возникающая в кольце}&\text{ потока через кольцо}\\
\hline
&\\
\hline
\end{array}\]
ЭДС индукции, возникающая в кольце – 2
ЭДС индукции: \[\xi_i=-\frac{\Delta \text{Ф}}{\Delta t}\] где \(\Delta \text{ Ф}\) – изменение потока вектора магнитной индукции, \(t\) – время. \[\xi_i=-S\cos \alpha \dfrac{\Delta B}{t},\] где \(\Delta B\) – изменение модуля вектора магнитной индукции, \(S\) – площадь рамки, \(\alpha\) – угол между нормалью к поверхности и вектором \(\vec{B}\). Значит ЭДС индукции уменьшается в 2 раза, так как площадь увеличивается в 2 раза, а скорость изменения модуля магнитной индукции уменьшается в 4 раза.
Скорость изменения магнитного потока через кольцо – 2
Изменение магнитного потока: \[\text{ Ф}=\Delta BScos\alpha\] Так как площадь увеличивается в 2 раза, а скорость изменения модуля магнитной индукции уменьшается в 4 раза, то и магнитный поток скорость изменения магнитного потока уменьшается.
Электрон движется по окружности в однородном магнитном поле. Как изменятся сила Лоренца, действующая на электрон, и период его обращения, если уменьшить его кинетическую энергию?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
\[\begin{array}{|c|c|}
\hline
\text{ Сила Лоренца, }&\text{ Период обращения }\\
\text{ действующая на электрон}&\\
\hline
&\\
\hline
\end{array}\]
Сила Лоренца, действующая на электрон – 2
Сила Лоренца: \[F_L=Bvqsin\alpha\] где \(B\) – модуль вектора магнитной индукции, \(v\) – скорость заряда, \(q\) – заряд, \(\alpha\) – угол между вектором магнитного поля и скоростью движения частицы. Кинетическая энергия находится по формуле: \[E=\dfrac{mv^2}{2},\] \(m\) – масса. Так как кинетическая энергия уменьшается, а масса остается неизменной, то уменьшается скорость частицы, а значит и уменьшается сила Лоренца, действующая на частицу.
Период обращения – 3
Второй закон Ньютона: \[F_L=ma_{\text{цс}}\] Распишем центростремительное ускорение, как \(\dfrac{v^2}{R}\) \[Bvq=\frac{mv^2}{R}\] Выразим радиус вращения \[R=\frac{mv}{Bq}\] Период же находится по формуле: \[T=\dfrac{2 \pi R }{v}\] Подставив в формулу периода радиус, получим \[T=\dfrac{2 \pi m}{Bq}\] Так как период не зависит от скорости, значит он не зависит от кинетической энергии (так как масса не изменяется), следовательно, период не изменяется.
Электрон движется по окружности в однородном магнитном поле. Как изменятся сила Лоренца, действующая на электрон, и период его обращения, если увеличить его кинетическую энергию?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
\[\begin{array}{|c|c|}
\hline
\text{ Сила Лоренца, }&\text{ Период обращения }\\
\text{ действующая на электрон}&\\
\hline
&\\
\hline
\end{array}\]
Сила Лоренца, действующая на электрон – 1
Сила Лоренца: \[F_L=Bvqsin\alpha\] где \(B\) – модуль вектора магнитной индукции, \(v\) – скорость заряда, \(q\) – заряд, \(\alpha\) – угол между вектором магнитного поля и скоростью движения частицы. Кинетическая энергия находится по формуле: \[E=\dfrac{mv^2}{2},\] \(m\) – масса. Так как кинетическая энергия увеличивается, а масса остается неизменной, то увеличивается скорость частицы, а значит и увеличивается сила Лоренца, действующая на частицу.
Период обращения – 3
Второй закон Ньютона: \[F_L=ma_{\text{цс}}\] Распишем центростремительное ускорение, как \(\dfrac{v^2}{R}\) \[Bvq=\frac{mv^2}{R}\] Выразим радиус вращения \[R=\frac{mv}{Bq}\] Период же находится по формуле: \[T=\dfrac{2 \pi R }{v}\] Подставив в формулу периода радиус, получим \[T=\dfrac{2 \pi m}{Bq}\] Так как период не зависит от скорости, значит он не зависит от кинетической энергии (так как масса не изменяется), следовательно, период не изменяется.
Проволочная обмотка генератора переменного тока равномерно вращается в постоянном магнитном поле. Угловую скорость вращения увеличивают. Как изменятся частота генерируемого переменного тока и амплитуда ЭДС индукции, действующей в обмотке?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
\[\begin{array}{|c|c|}
\hline
\text{ Частота переменного тока }&\text{ ЭДС индукции в обмотке}\\
\hline
&\\
\hline
\end{array}\]
Частота переменного тока – 1
Так как угловая скорость рамки увеличивается, то и полный оборот вокруг оси она будет совершать быстрее, а это означает, что период обращения уменьшится, период и частота связаны формулой: \[\nu=\dfrac{1}{T}\] Так как период уменьшается, то частота увеличивается.
ЭДС индукции в обмотке – 1
\[\xi_i=-\frac{\Delta \text{Ф}}{\Delta t}\] где \(\Delta \text{ Ф}\) – изменение потока вектора магнитной индукции, \(t\) – время. \[\xi_i=-S\cos \alpha \dfrac{\Delta B}{t},\] где \(\Delta B\) – изменение модуля вектора магнитной индукции, \(S\) – площадь рамки, \(\alpha\) – угол между нормалью к поверхности и вектором \(\vec{B}\). Так как увеличивается скорость движения рамки, то и увеличивается скорость изменения потока, а значит и увеличивается ЭДС индукции в обмотке.
Маленький шарик массой \(m\) и зарядом \(q\), закрепленный тонкой непроводящей нитью, вращается на гладкой поверхности по окружности с постоянной по модулю скоростью \(v\) в однородном магнитном поле \(\vec{B}\). Как изменятся сила Лоренца и сила натяжения нити, если увеличить массу шарика.
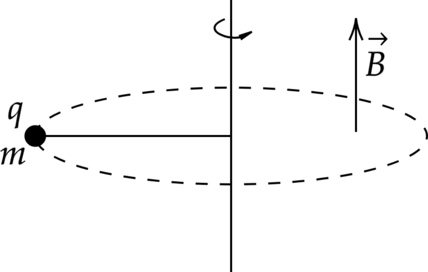
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится.
\[\begin{array}{|c|c|}
\hline
\text{ Сила Лоренца }&\text{ Сила натяжения нити}\\
\hline
&\\
\hline
\end{array}\]
Сила Лоренца – 3
Сила Лоренца находится по формуле: \[F_L=Bvqsin\alpha\] где \(B\) – модуль вектора магнитной индукции, \(v\) – скорость заряда, \(q\) – заряд, \(\alpha\) – угол между вектором магнитного поля и скоростью движения частицы. Она не зависит от массы, а значит она неизменна.
Сила натяжения нити – 1
Второй закон Ньютона: \[\vec{F_L}+\vec{T}=ma\] где \(T\) – сила натяжения нити. Согласно правилу левой руки, сила Лоренца будет направлена вдоль радиус-вектора, выходящего из центра окружности. Тогда Второй закон Ньютона можно переписать в виде \[T=ma \pm F_L\] Так как сила Лоренца не зависит от массы, то сила натяжения нити будет увеличиваться.


