Кинематика (страница 2)
Готовиться с нами - ЛЕГКО!

Установите соответствие между зависимостью проекции скорости тела от времени и зависимостью проекции перемещения этого тела от времени для одного и того же движения (все величины выражены в СИ). \[\begin{array}{|c|c|} \hline \text{Проекция скорости}&\text{ Проекция перемещения}\\ \hline &\\ \text{А)} \upsilon_x=3-2t& \text{1)} S_x=5t+2t^2 \\ \text{Б)} \upsilon_x=5+4t &\text{2)} S_x=5t+4t^2\\ &\text{3)} S_x=3t-2t^2\\ &\text{4)} S_x=3t-t^2\\ \hline \end{array}\] Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: \[\begin{array}{|c|c|} \hline \text{А}&\text{Б}\\ \hline & \\ \hline \end{array}\]
Скорость – это производная от координаты (перемещения) по времени. Возьмем производную от четырех формул, а дальше сделаем соответствие:
1) \(\displaystyle S_x=5t+2t^2\)
\[\upsilon_x=S'(x)=5+4t\] Ответ – Б
2) \(\displaystyle S_x=5t+4t^2\)
\[\upsilon_x=S'(x)=5+8t\] 3) \(\displaystyle S_x=3t-2t^2\)
\[\upsilon_x=S'(x)=3-4t\] 4) \(\displaystyle S_x=3t-t^2\)
\[\upsilon_x=S'(x)=3-2t\] Ответ – А
Установите соответствие между зависимостью координаты материальной точки (все значения выражены в СИ) и значениями его начальной координаты и проекцией ускорения на ось \(Ox\).
К каждой позиции первого столбца подберите подходящую позицию из второго столбца. В ответ укажите последовательность чисел.
\[\begin{array}{|c|c|} \hline \text{УРАВНЕНИЕ ДВИЖЕНИЯ:} & \text{НАЧАЛЬНАЯ КООРДИНАТА, УСКОРЕНИЕ:}\\ \hline \text{А)}\ x = 2+5t -3t^2&1)\ x_0 = 0, a_x =7\text{ м/с$^2$}\\ \text{Б)}\ x = 7t &2)\ x_0 = 2\text{ м/с},a_x = -6\text{ м/с$^2$}\\ &3)\ x_0 = 2\text{ м/с},a_x =-3\text{ м/с$^2$}\\ &4)\ x_0 = 0,a_x = 0\text{ м/с$^2$}\\ \hline \end{array}\]
\[\begin{array}{|c|c|} \hline \text{A}&\text{Б}\\ \hline &\\ \hline \end{array}\]
Основное уравнение кинематики показывает зависимость координаты \(x\) от времени \(t\): \[x = x_0 + \upsilon_{0x}t+ \dfrac{a_xt^2}{2}\]
где \(x_0\) – начальная координата, \(\upsilon_{0x}\) – проекция начальной скорости на ось \(Ox\), \(a_x\) – проекция ускорения на ось \(Ox\).
A – 2
Рассмотрим данное уравнение: \[x = 2+5t -3t^2\]
Сопоставив его с основным уравнением кинематики, можно увидеть, что \(x_0 = 2\text{ м},a_x = -6\text{ м/с$^2$}\).
Б – 4
Рассмотрим данное уравнение: \[x = 7t\]
Сопоставив его с основным уравнением кинематики, можно увидеть, что \(x_0 = 0\text{ м},a_x = 0\text{ м/с$^2$}\) (тело движется прямолинейно, без ускорения).
Для условий 1 и 3 уравнения будут выглядеть соответсвенно: \[x = 3,5t^2\] \[х = 2+\upsilon_0t -1,5t^2\]
Тело движется вдоль оси \(Ox\) из начала координат с постоянным ускорением. Направления начальной скорости и ускорения \(a\) тела указаны на рисунке.
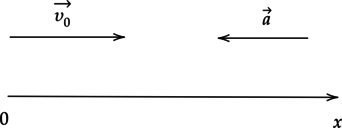
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные под соответствующими буквами. \[\begin{array}{cc} \text{ Физические величины}&\text{ Формулы}\\ \text{А) Координата x тела в момент времени t;}& \text{ 1) } \displaystyle v_0t+\frac{at^2}{2} \\ \text{Б) Скорость $v_x$ тела в момент времени t.}& \text{ 2) } \displaystyle v_0t - \frac{at^2}{2}\\ & \text{ 3) } \displaystyle v_0 - at\\ &\text{ 4) } \displaystyle v_0 +at\\ \end{array}\]
\[\begin{array}{|c|c|} \hline \text{ A }&\text{ Б }\\ \hline &\\ \hline \end{array}\]
Проекция вектора ускорения \(\vec{a}\) на ось \(Ox\): \(a_x=-a\). Проекция вектора начальной скорости \(\vec{\upsilon_{0}}\) на ось \(Ox\): \(v_x=v_0\). Так как тело начинает движение из начала координат, координата тела \(x\) в момент времени \(t\): \[x=\upsilon_{0}t - \dfrac{at^{2}}{2}\]
(А — 2)
Скорость \(\upsilon_{x}\) тела в момент времени t: \[v_x=v_0 - at\]
(Б — 3)
Тело первую половину пути проходит со скоростью \(\upsilon_{1}\), а вторую – со скоростью \(\upsilon_{2}\). Как изменится средняя скорость на всём пути, если
\[\begin{array}{cc}
\text{А) увеличить весь путь в 2 раза, }& \text{ 1) увеличится в 2 раза }\\
\text{Б) увеличить каждую из скоростей в 2 раза, }& \text{ 2) увеличится в 4 раза }\\
& \text{ 3) уменьшится в 2 раза }\\ & \text{ 4) уменьшится в 4 раза } \\
&\text{ 5) не изменится}\\
\end{array}\]
Запишите в таблицу выбранные цифры под соответствующими буквами.
\[\begin{array}{|c|c|}
\hline
\text{ A }&\text{ Б }\\
\hline
&\\
\hline
\end{array}\]
Средняя скорость на всём пути: \[\displaystyle \upsilon_{\text{ ср}} = \frac{S_{1} + S_{2}}{t_{1 } + t_{2}}.\]
Пусть весь путь \(S = 2l\), тогда \(S_{1} = l\), \(S_{2} = l\), \(t_{1} = \dfrac{l}{\upsilon_{1}}\), \( t_{2} = \dfrac{l}{\upsilon_{2}}\).
Отсюда \[\displaystyle \upsilon_{\text{ ср}} = \dfrac{2l}{\dfrac{l}{\upsilon_{1}} + \dfrac{l}{\upsilon_{2}}} = \dfrac{2\upsilon_{1}\upsilon_{2}}{\upsilon_{1} + \upsilon_{2}}.\]
Значит средняя скорость зависит только от скоростей \(\upsilon_{1}\) и \(\upsilon_{2}\) на каждой из половин пути и не зависит от длины самого пути, поэтому вопросу А соответствует 5.
В других случаях, поскольку \(\upsilon_{1}\) и \(\upsilon_{2}\) изменяются в одинаковое число раз, средняя скорость изменяется пропорционально изменению одной из скоростей \(\Rightarrow\) Б = 1
Четыре байкера движутся по прямому шоссе с одинаковыми скоростями \(\upsilon\), 1 и 2 – на концерт (в одном направлении (вдоль оси \(Ox\))), а 3 и 4 – им навстречу с концерта. Определите проекции их относительных скоростей на ось \(Ox\).
\[\begin{array}{cc}
\text{А) 2 относительно 1 }& \text{ 1) $\upsilon$ }\\
\text{Б) 1 относительно 3 }& \text{ 2) $2\upsilon$ }\\
& \text{ 3)$-\upsilon$ }\\
& \text{ 4)$-2\upsilon$ }\\
&\text{ 5) 0}\\
\end{array}\]
Запишите в таблицу выбранные цифры под соответствующими буквами.
\[\begin{array}{|c|c|}
\hline
\text{ A }&\text{ Б }\\
\hline
&\\
\hline
\end{array}\]
Проекция на ось \(Ox\) скорости любого байкера из первой пары относительно любого из второй пары: \[\upsilon_{\text{отн1}}' = \upsilon - ( -\upsilon) = 2\upsilon\]
И наоборот, проекция относительной скорости любого байкера из второй пары в системе отсчёта первой: \[\upsilon_{\text{отн2}}' = -\upsilon -\upsilon = -2\upsilon\]
Внутри каждой из пары байкеры покоятся друг относительно друга, т.е. для них относительная скорость равна нулю.
Бэтмобиль, двигаясь ускоренно, имел в начальной точке трассы скорость \(\upsilon_{0}\), через некоторое время в конечной точке трассы скорость \(\upsilon_{2}\). Укажите выражения для:
\[\begin{array}{cc}
\text{А) скорости бэтмобиля на половине этого расстояния }& \text{ 1) $\dfrac{(\upsilon_{0} + \upsilon_{2})}{2}$ }\\
\text{Б) средней скорости бэтмобиля на всём пути }& \text{ 2) $\sqrt{\dfrac{(\upsilon_{0}^{2} + \upsilon_{2}^{2})}{2} }$ }\\
& \text{ 3)$\dfrac{(\upsilon_{2} - \upsilon_{0})}{2}$ }\\
& \text{ 4)$\sqrt{\dfrac{(\upsilon_{2}^{2} - \upsilon_{0}^{2})}{2} }$ }\\
\end{array}\]
Запишите в таблицу выбранные цифры под соответствующими буквами.
\[\begin{array}{|c|c|}
\hline
\text{ A }&\text{ Б }\\
\hline
&\\
\hline
\end{array}\]
При равноускоренном движении с начальной скоростью \(\upsilon_{0}\) весь путь будет равен: \[S = \dfrac{\upsilon_{2}^{2} - \upsilon_{0}^{2}}{2a}\]
для первой половины пути: \[\dfrac{S}{2} =\dfrac{\upsilon_{1}^{2} - \upsilon_{0}^{2}}{2a}\]
где \(v_{1}\) — скорость на половине пути
\[2(v_1^2-v_0^2)=v_2^2-v_0^2\]
\[\upsilon_{1} = \sqrt{\dfrac{(\upsilon_{0}^{2} + \upsilon_{2}^{2})}{2}}\]
Скорость при равноускоренном движении меняется линейно: \[v=v_0+at\]
Средняя величина при линейной зависимости определяется как среднее арифметическое начального и конечного значения. Средняя скорость на всём пути равна: \[\upsilon_{\text{ ср}} = \dfrac{(\upsilon_{0} + \upsilon_{2})}{2}\]
Автомобиль движется вдоль оси \(Ox\), при этом его координата изменяется с течением времени в соответствии с формулой \(x(t) = 6 - 8t^{2}\) (все величины выражены в СИ).
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
\[\text{ГРАФИКИ}\] 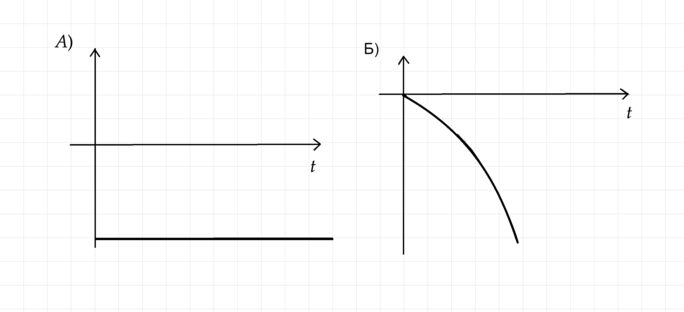
\[\text{ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ}\] 1) проекция скорости автомобиля \(\upsilon_{x}\)
2) проекция перемещения автомобиля \(S_{x}\)
3) проекция ускорения автомобиля \(a_{x}\)
4) модуль равнодействующей \(\vec{F}\) сил, действующих на автомобиль.
\[\begin{array}{|c|c|} \hline \text{ A }&\text{ Б }\\ \hline &\\ \hline \end{array}\]
1) Проекцию скорости \(\upsilon_{x}\) можно найти как производную от \(x\): \[\upsilon_{x} = x^\prime =(6 - 8t^{2})^\prime = -16t.\]
график будет выглядеть, как прямая идущая из нуля и постоянно убывающая \(\Rightarrow\) (1) неподходит.
2) Проекция перемещения — это конечная координата минус начальная
\[S_{x} = x - x_{0};\: x_{0} = 6\: \Rightarrow\: S_{x} = -8t^{2}.\] график — одна из ветвей параболы, идущей из начала координат и направленных вниз \(\Rightarrow\) Б — 2.
3) Проекция ускорения — производная по времени от проекции скорости: \[a_{x} = \upsilon_{x}^\prime = (-16t)^\prime = -16.\] график будет выглядеть, как прямая линия параллельная оси t и идущая ниже нуля \(\Rightarrow\) А — 3.
4) \(F = ma = const,\: m > 0,\: a = |a_{x}| = 16\: \Rightarrow\: F > 0\) \(\Rightarrow\) не подходит.



