МКТ и Термодинамика

Молекулярно-кинетическая теория. Газовые законы

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: МКТ и Термодинамика

Теоретическая справка

#597

Основные формулы

Основное уравнение МКТ для идеального газа:

-- p = 1m0nv2 3

p= 2nEk- 3

1 -- p = 3ρv2

p= nkT

Cредняя кинетическая энергия поступательного движения:

-- Ek-= m0-v2 2

Закон Дальтона:

pсмеси = p1 +p2+ ⋅⋅⋅+pn

Уравнение состояния идеального газа:

pV = νRT

pV = m-RT μ

ρ p = μRT

Количество вещества:

m N ν = μ-= N-- A

Основные положения МКТ. Основные понятия

Основные положения МКТ

Любое вещество состоит из мельчайших частиц — молекул и атомов. Они расположены в пространстве дискретно, то есть на некоторых расстояниях друг от друга.
Атомы или молекулы вещества находятся в состоянии беспорядочного движения, которое никогда не прекращается.
Атомы или молекулы вещества взаимодействуют друг с другом силами притяжения и отталкивания, которые зависят от расстояний между частицами.

Модель идеального газа. Основное уравнение МКТ

Идеальный газ — это газ, частицы которого являются не взаимодействующими между собой на расстоянии материальными точками, испытывающими абсолютно упругие соударения друг с другом и со стенками сосуда.

$PIC$

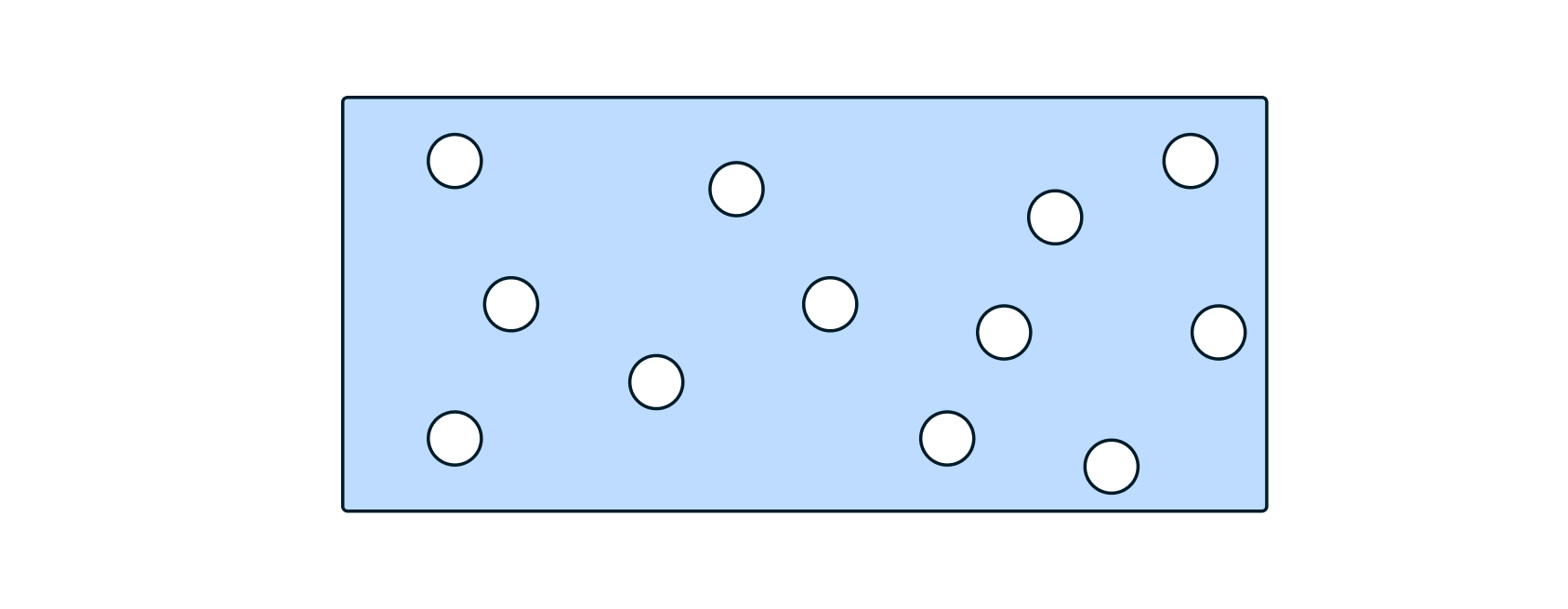
В кинетической модели молекулы идеального газа рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Из-за соударений молекулы оказывают давление на стенки. Состояние такой системы описывается основным уравнением МКТ идеального газа:

1 -2 p= 3m0n v ,

где $p$ — давление, $m0$ — масса одной молекулы, $n$ — концентрация, $v$ — средняя квадратичная скорость.

Единицы измерения: $[p]=$ Па (паскаль).

Пусть в системе «идеальный газ — сосуд» находится $m$ молекул. Тогда средняя квадратичная скорость $v$ определяется через скорость этих молекул следующим образом:

∘ -2---2-------2- v = v1-+v2 +-⋅⋅⋅+vm m

Единицы измерения: $- [v]=$ м/с (метры в секунду).

Для простоты далее будем считать, что все молекулы системы одинаковой массы и движутся с одинаковой по модулю скоростью, равной $v$ средней квадратичной.

Для концентрации $n$ имеем:

m n = V ,

где $m$ — число молекул в объеме $V$ .

Единицы измерения: $[n]=$ кг/м $3$ (килограмм на кубический метр).

Понятие кинетической энергии

МКТ рассматривает хаотичное движение молекул (еще его называют тепловым движением). Каждая молекула газа при таком движении имеет некоторую скорость, значит и обладает кинетической энергией. У кинетической энергии молекул есть важная физическая интерпретация - она характеризует температуру газа. Иными словами, температура газа показывает, насколько быстро двигаются молекулы.

Кинетическая энергия поступательного движения одной молекулы:

3 Eк = 2kT,

где $k$ — постоянная Больцмана, $T$ — абсолютная температура.

Данная формула показывает, что температура тела является характеристикой кинетической энергии поступательного движения каждой молекулы в отдельности.

Понятие средней квадратичной скорости

Получим выражение для средней квадратичной скорости одной молекулы массой $m0$ . Кинетическая энергия движения одной молекулы по определению:

m0v2 Eк =--2--

Зная кинетическую энергию поступательного движения одной молекулы, запишем:

m0v2 3 --2--= 2kT

Получили формулу для средней квадратичной скорости движения одной молекулы:

∘ ---- v = 3kT- m0

Вывод основного уравнения МКТ

В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара (подчиняются законам Ньютона).

Используя модель идеального газа, вычислим давление газа на стенку сосуда. Во время взаимодействия молекулы со стенкой сосуда возникают силы, подчиняющиеся третьему закону Ньютона. В результате, проекция $vx$ скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция $vy$ скорости, параллельная стенке, остается неизменной.

$PIC$

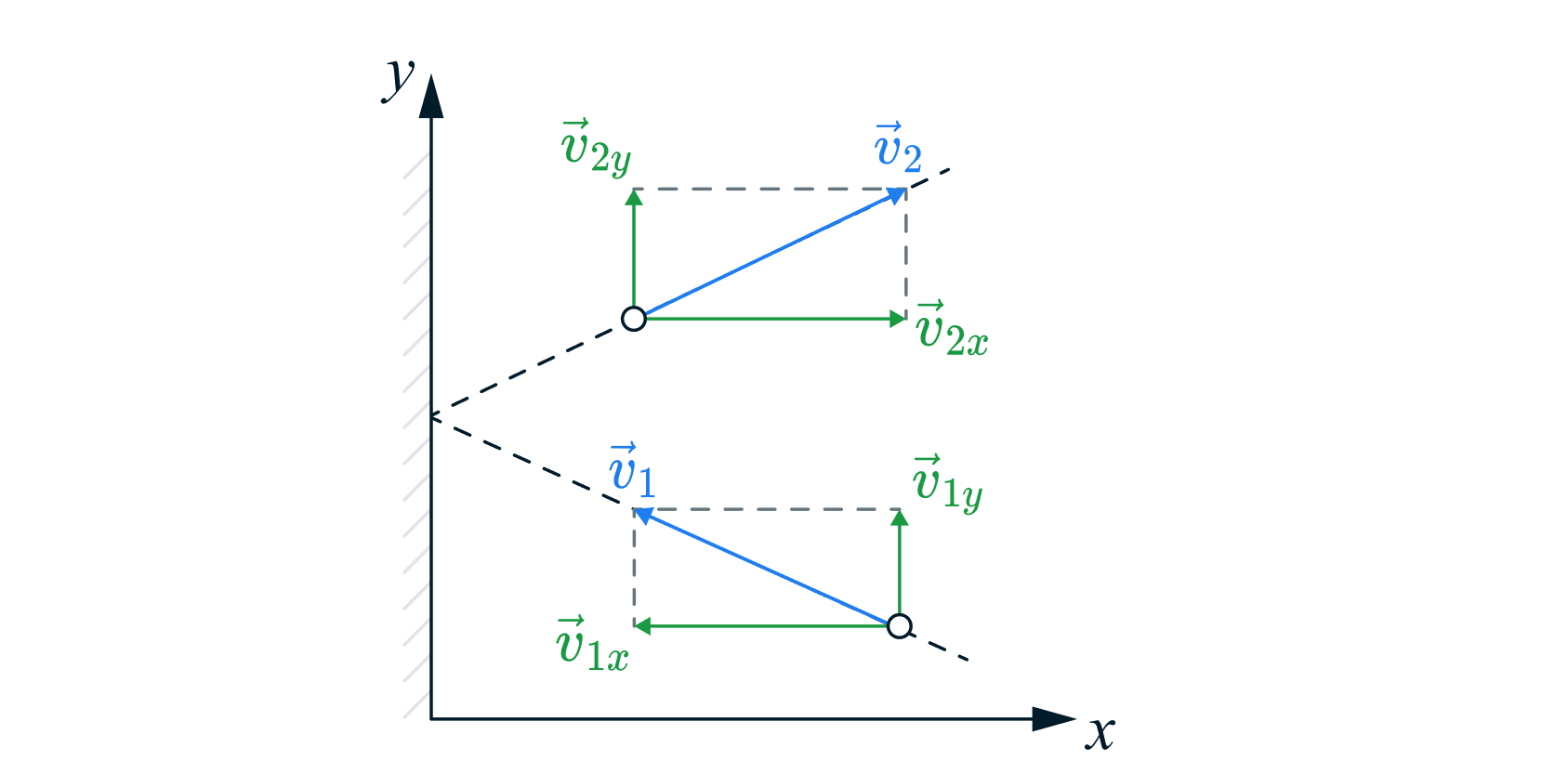
Таким образом, изменение проекции импульса молекулы на ось $x$ после удара будет равно $2m0vx$ , где $m0$ — масса молекулы.

Выделим на стенке некоторую площадку $S$ (см. рисунок). За время $Δt$ с этой площадкой столкнутся все молекулы, имеющие проекцию скорости $vx$ , направленную в сторону стенки, и находящиеся в цилиндре с основанием площади $S$ и высотой $vxΔt$ .

$PIC$

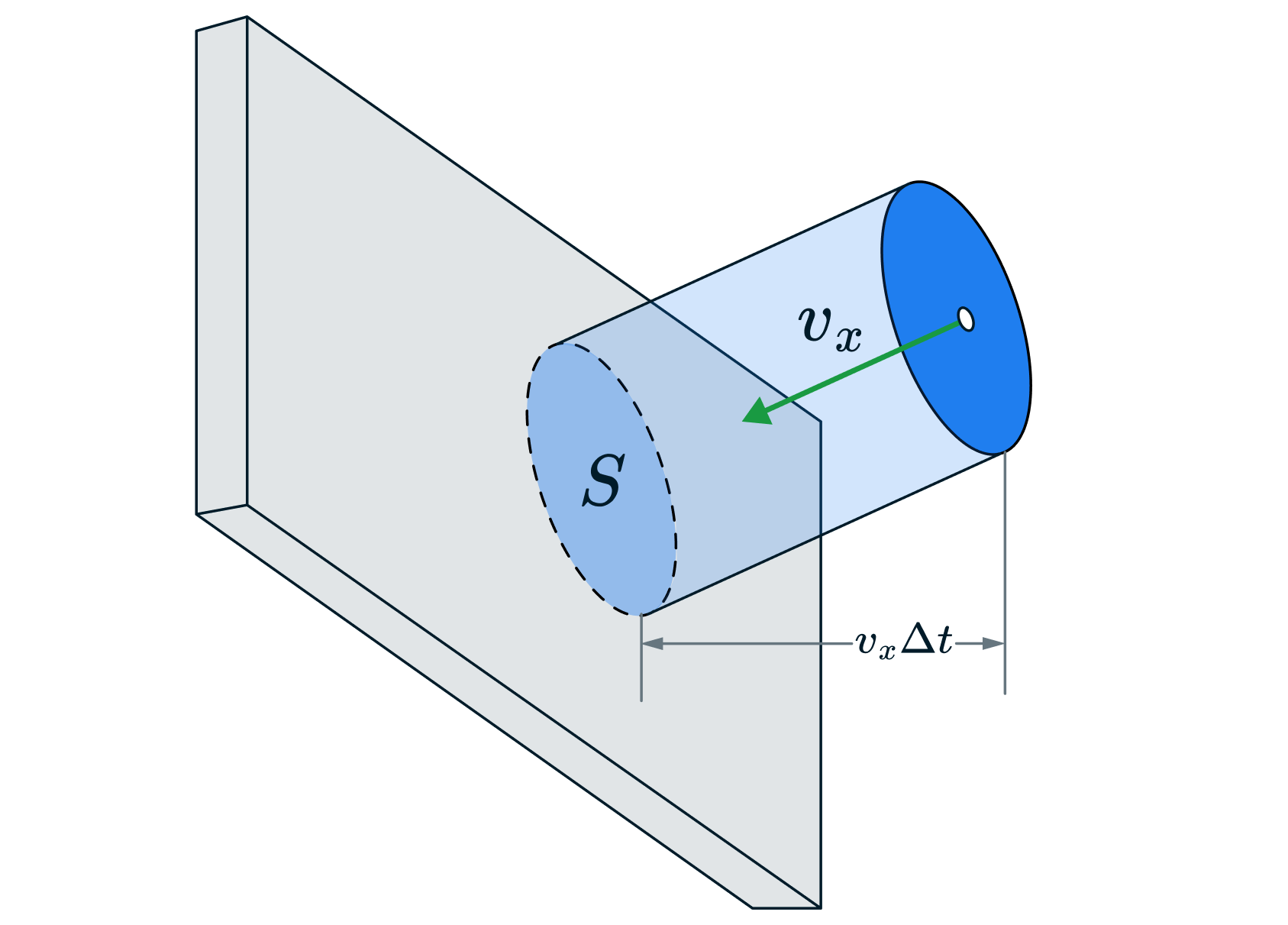
Пусть в единице объема сосуда содержатся $n$ молекул; тогда число молекул в объеме цилиндра равно $nSv Δt x$ . Но из этого числа лишь половина движется в сторону стенки, а другая половина движется в противоположном направлении и со стенкой не сталкивается.

Следовательно, число ударов молекул о площадку $S$ за время $Δt$ равно $1∕2nSvxΔt$ .

Поскольку каждая молекула при столкновении со стенкой изменяет свой импульс на величину $2m0vx$ , то полное изменение импульса всех молекул, столкнувшихся за время $Δt$ с площадкой $S$ , равно $nm0v2xS Δt$ .

По законам механики это изменение импульса всех столкнувшихся со стенкой молекул происходит под действием импульса силы $FΔt$ , где $F$ — некоторая средняя сила, действующая на молекулы со стороны стенки на площадке $S$ . Но по 3-му закону Ньютона такая же по модулю сила действует со стороны молекул на площадку $S$ . Поэтому можно записать:

FΔt = nm0v2xSΔt

Разделив обе части на $SΔt$ , получим:

p = F-= nm0v2x, S

где $p$ — давление газа на стенку сосуда.

При выводе этого соотношения предполагалось, что все $n$ молекул, содержащихся в единице объема газа, имеют одинаковые проекции скоростей на ось $X$ . На самом деле, это не так.

В результате многочисленных соударений молекул газа между собой и со стенками в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям. При этом все направления векторов скоростей молекул оказываются равноправными, а модули скоростей и их проекции на координатные оси подчиняются определенным закономерностям.

Теперь формулу для давления газа можно записать в виде

-- p= nm0v2x

Так как все направления для векторов скоростей молекул равновероятны, среднее значение квадратов их проекций на координатные оси равны между собой:

-- -- -- -- v2x =v2y = v2z = 1v2 3

Последнее равенство вытекает из формулы:

v2x+ v2y + v2z = v2

Формула для среднего давления газа на стенку сосуда запишется в виде

-- - 1 -2 2 m0v2- 2 --- p =p = 3nm0v = 3n 2 = 3nEk,

где $Ek-$ — средняя кинетическая энергия молекул — среднее арифметическое их кинетических энергий.

Таким образом, давление газа равно двум третьим от средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.

Варианты основного уравнения МКТ

Выведенное ранее основное уравнение МКТ имеет вид:

$p = 1m0nv2 3$
Существует связь давления и средней кинетической энергии молекул, которая тоже является вариантом записи основного уравнения МКТ:

$2 p= 3nEк$
Подставим теперь вместо $Eк$ выражение для кинетической энергии поступательного движения одной молекулы и получим:

$p= nkT$

Температурная шкала Кельвина. Понятие количества вещества

В МКТ для температур принято использовать абсолютную шкалу Кельвина.

Единицы измерения: $[T]=$ К (кельвин).

Перевод из шкалы Цельсия в шкалу Кельвина:

T = t+ 273,

где $t$ — температура в градусах Цельсия.

У шкалы Кельвина существует абсолютный ноль, служащий началом отсчета абсолютной температурной шкалы:

o 0К = − 273 С

В классической физике принято считать, что при температуре 0 кельвин молекулы перестают двигаться и тепловое движение прекращается.

Количество вещества

Работать с массами молекул зачастую неудобно. В связи с этим вводится понятие количества вещества $ν$ .

Единицы измерения: $[ν]=$ моль.

1 моль любого вещества содержит одно и то же число молекул, равное числу Авогадро.

23 −1 NA =6,023⋅10 мол ь

Количество вещества можно найти по формулам:

ν = N--= m-, NA μ

где $N$ — количество молекул (в штуках), $m$ — масса вещества, $μ$ — молярная масса вещества.

Молярная масса — масса одного моля вещества.

Единицы измерения: $[μ]=$ кг/моль.

Молярную массу можно найти, используя таблицу Менделеева. Обратите внимание, в большинстве случаев молярная масса в таблице приведена в граммах на моль.

Рассмотрим молекулу воды: она содержит два атома водорода и один атом кислорода ( $H2O$ .)

Атомная масса водорода из таблицы Менделеева — 1, атомная масса кислорода — 16, причем атом водорода присутствует в молекуле в количестве 2 штук. Исходя из этого, найдем молярную массу молекулы воды: $μH2O = 2 ⋅1 + 1⋅16=$ 18 г/моль. В системе СИ: $−3 μH2O =18 ⋅10$ кг/моль.

Уравнение состояния идеального газа. Изопроцессы

Уравнение Клапейрона-Менделеева

Уравнение Клапейрона-Менделеева, или уравнение состояния идеального газа, связывает три макроскопических параметра газа ( $p,$ $V$ и $T$ ).

pV = νRT,

где $p$ — давление газа, $V$ — его объем, $ν = m∕μ$ — количество вещества ( $m$ — масса газа, $μ$ — его молярная масса), $T$ — абсолютная температура газа, $R = 8,31 ---Д-ж---- м оль ⋅ К$ — универсальная газовая постоянная.

Уравнение Клапейрона-Менделеева также можно записать в виде

pV = m-RT μ

Понятие изопроцессов

Изопроцессы — термодинамические процессы, во время которых количество вещества газа и один из параметров состояния: давление, объём или температура — остаются неизменными.

Изотермический процесс, $T = const$
Из уравнения Клапейрона-Менделеева заключаем: $pV = const$
Отсюда закон Бойля-Мариотта

$p1V1 = p2V2$

Здесь и далее параметры с индексом 1 обозначают величины в начале изопроцесса, а с индексом 2 — в конце.
Изохорный процесс, $V = const$
По аналогии получаем закон Шарля:

$p1 T1 p2 = T2$
Изобарный процесс, $P = const$
Для него закон Гей-Люссака:

$V1 T1 V2 = T2$

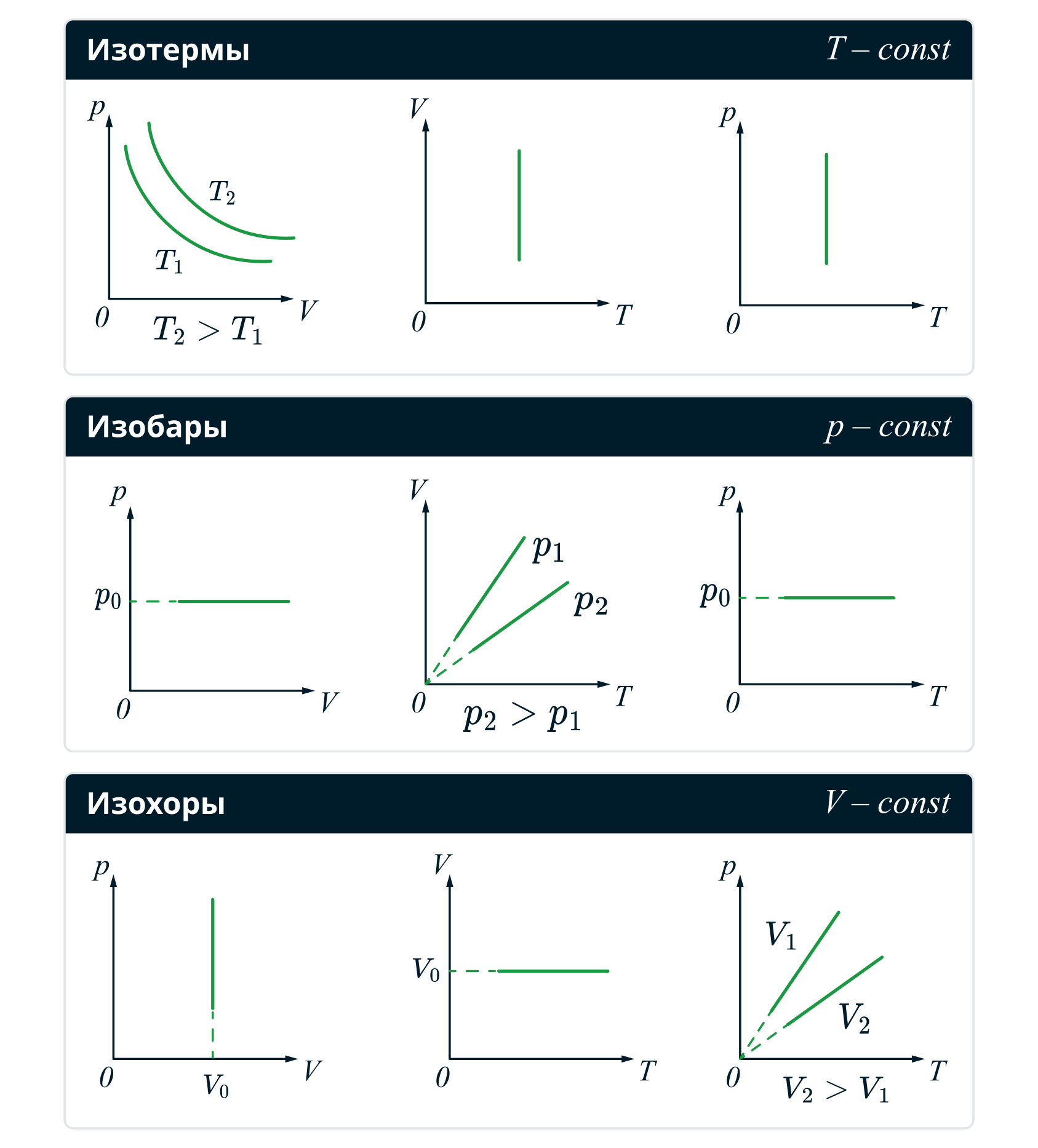
Графики изопроцессов

$PIC$

Предыдущая справка

Следующая справка