Основные формулы

Равномерное прямолинейное движение

Перемещение:

\[ S_x = \upsilon_x t \]

Зависимость координаты от времени:

\[ x(t) = x_0 + \upsilon_x t \]

Равноускоренное прямолинейное движение

Ускорение тела:

\[ a_x = \dfrac{\Delta \upsilon_x}{\Delta t} = \dfrac{\upsilon_{\text{к}x} - \upsilon_{0x}}{\Delta t} \]

Зависимость скорости от времени:

\[ v_{x}(t) = v_{0x} + a_x t \]

Зависимость координаты от времени:

\[ x(t) = x_0 + v_{0x} t + \dfrac{a_x t^2}{2} \]

Перемещение:

\[ S_x = \upsilon_{0x} t + \dfrac{a_x t^2}{2} \]

Перемещение, «формула без времени»:

\[ S_x = \dfrac{\upsilon_{\text{к}x}^2 - \upsilon_{0x}^2}{2a_x} \]

Перемещение, «формула без ускорения»:

\[ S_x = \dfrac{1}{2} (v_{0x} + v_{\text{к}x}) t \]

Механическое движение

Механическое движение тела — изменение положения тела в пространстве относительно других тел с течением времени. При механическом движении тела взаимодействуют по законам механики.

Кинематика описывает геометрические свойства движения без учета причин, которые его вызывают. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел во времени.

Материальная точка — это тело, размеры которого очень малы по сравнению с расстоянием, которое оно прошло, поэтому этими размерами можно пренебречь. В кинематике все тела принято рассматривать как материальные точки.

Основные понятия

• Траектория — линия, вдоль которой движется тело.

• Путь — длина участка траектории, пройденного телом за определенный промежуток времени.

• Радиус-вектор — вектор, проведенный из начала координат в место расположения материальной точки. Положение материальной точки в пространстве задается радиус-вектором.

• Перемещение — вектор, соединяющий начальное и конечное положение тела.

• Система отсчета — тело отсчета (начало координат) вместе с жестко связанной с ним системой координат и часами.

Кинематические характеристики движения материальной точки

Перемещение — вектор, соединяющий два последовательных положения материальной точки на траектории. Перемещение является вектором-разностью радиус-векторов конечного и начального положений тела.

Графический метод нахождения перемещения и пройденного пути: для определения проекции перемещения \(S_x\) нужно найти численно равную ей площадь под графиком проекции скорости \(v_x(t)\).

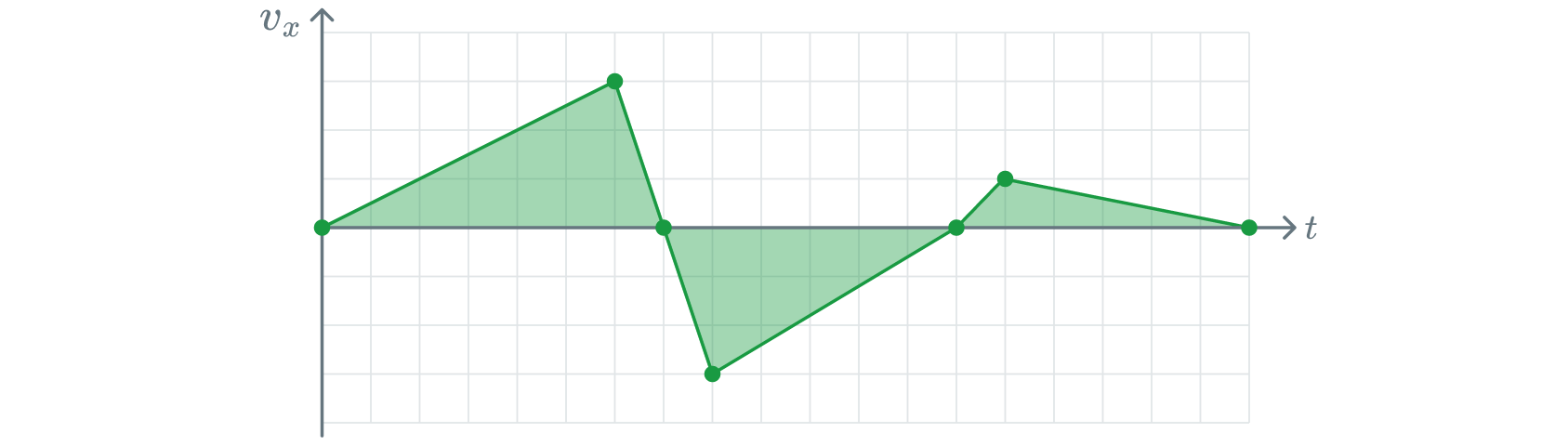
Скорость — векторная физическая величина, которая характеризует быстроту изменения положения материальной точки в пространстве с течением времени.

\[ \vec{v} = \frac{\Delta \vec{x}}{\Delta t} \]

Единицы измерения:

\([v] = \text{м/с}\) (метр в секунду).

Вектор скорости — это первая производная от радиус-вектора по времени.

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости по величине и по направлению.

\[ \vec{a} = \dfrac{\Delta \vec{v}}{\Delta t} = \dfrac{\vec{v}_\text{к} - \vec{v}_0}{\Delta t} \]

где \(v_\text{к}\) и \(v_0\) — конечная и начальная скорость соответственно.

В проекции на ось \(x\):

\[ a_x = \dfrac{v_{\text{к}x} - v_{0x}}{\Delta t} \]

где \(v_{\text{к}x}\) и \(v_{0x}\) — проекции конечной и начальной скорости на ось \(x\) соответственно.

Единицы измерения:

\([a] = \text{м/с}^2\) (метр в секунду за секунду).

Вектор ускорения — это первая производная от скорости по времени и вторая производная от радиус-вектора по времени.

Вектор ускорения сонаправлен с вектором скорости при равноускоренном движении и противоположно направлен при равнозамедленном движении.

Прямолинейное равномерное движение

Прямолинейное равномерное движение (ПРД) — движение, при котором тело за равные промежутки времени совершает одинаковые перемещения.

Траектория ПРД — прямая. При этом скорость остается постоянной \(\vec{v} = \vec{const}\).

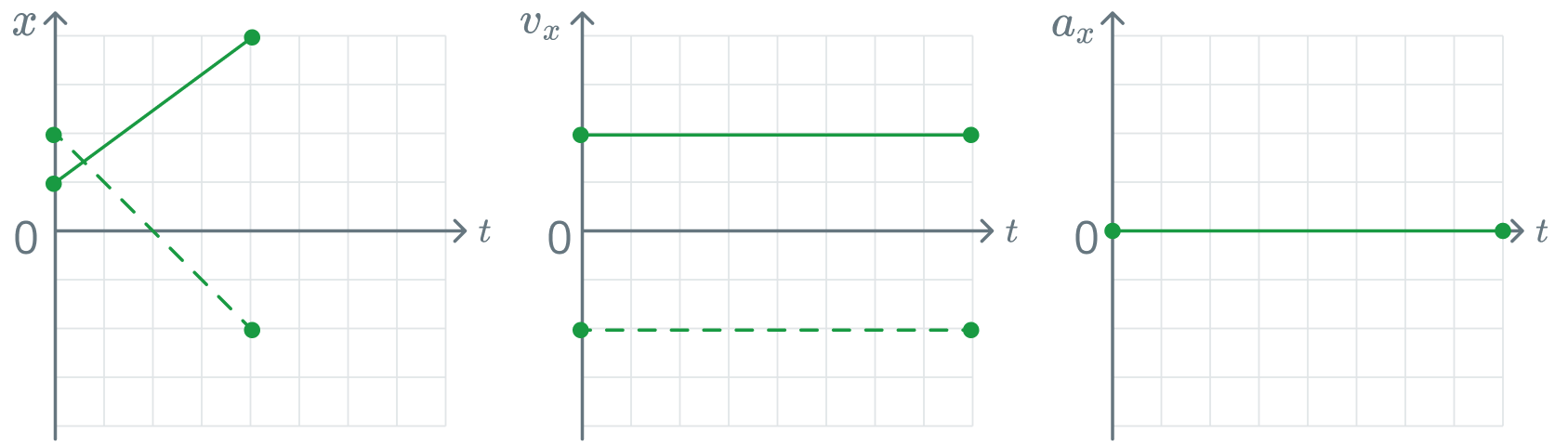
Уравнение движения материальной точки:

\[ \vec{r}(t) = \vec{r}_0 + \vec{v} t \]

Скорость движения материальной точки:

\[ \vec{v} = \text{const} \]

Ускорение материальной точки:

\[ \vec{a} = \vec{0} \]

Пройденный путь:

\[ S = v t \]

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение (ПРУД) материальной точки — движение с постоянным вектором ускорения \(\vec{a} = \vec{const}\). Траекторией ПРУД является парабола.

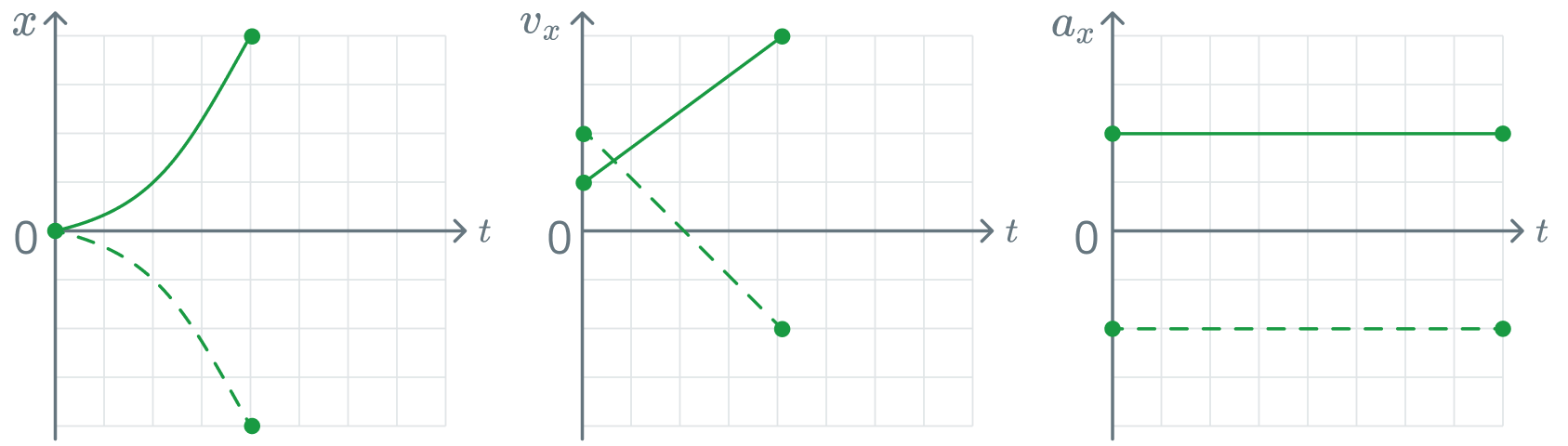
Уравнение движения материальной точки:

\[ \vec{r}(t) = \vec{r}_0 + \vec{v}_0 t + \dfrac{\vec{a} t^2}{2} \]

Скорость движения материальной точки:

\[ \vec{v}(t) = \vec{v}_0 + \vec{a} t \]

Ускорение материальной точки:

\[ \vec{a} = \vec{const} \]

Перемещение:

\[ S_x = v_{0x} t + \dfrac{a_x t^2}{2} \]

Перемещение, «формула без времени»:

\[ 2 \vec{a} \vec{S} = \vec{v}^2 - \vec{v}_0^2 \]

Перемещение, «формула без ускорения»:

\[ \vec{S} = \dfrac{(\vec{v} + \vec{v}_0) t}{2} \]

Для вывода формул:

\[ a_x = \dfrac{v_{\text{к}x} - v_{0x}}{t} \;\; \Rightarrow \;\; v_x = v_{0x} + a_x t \]

Сумма площадей прямоугольника и треугольника под графиком скорости:

\[ S = S_\text{прямоуг} + S_\text{треуг} \]

\[ S = v_{0x} t + \dfrac{a_x t^2}{2} \]

Формула без ускорения (трапеция):

\[ S = \dfrac{(v_{0x} + v_x) t}{2} \]

Векторное представление:

\[ \vec{S} = \dfrac{\vec{v}_0 + \vec{v}}{2} t \]

Домножим обе части на \(\vec{a}\):

\[ \vec{S} \vec{a} = \dfrac{\vec{v}_0 + \vec{v}}{2} (\vec{v} - \vec{v}_0) \]

Упрощаем через разность квадратов:

\[ 2 \vec{a} \vec{S} = \vec{v}^2 - \vec{v}_0^2 \]

Скалярное произведение:

\[ 2 a S \cos\alpha = v^2 - v_0^2 \]

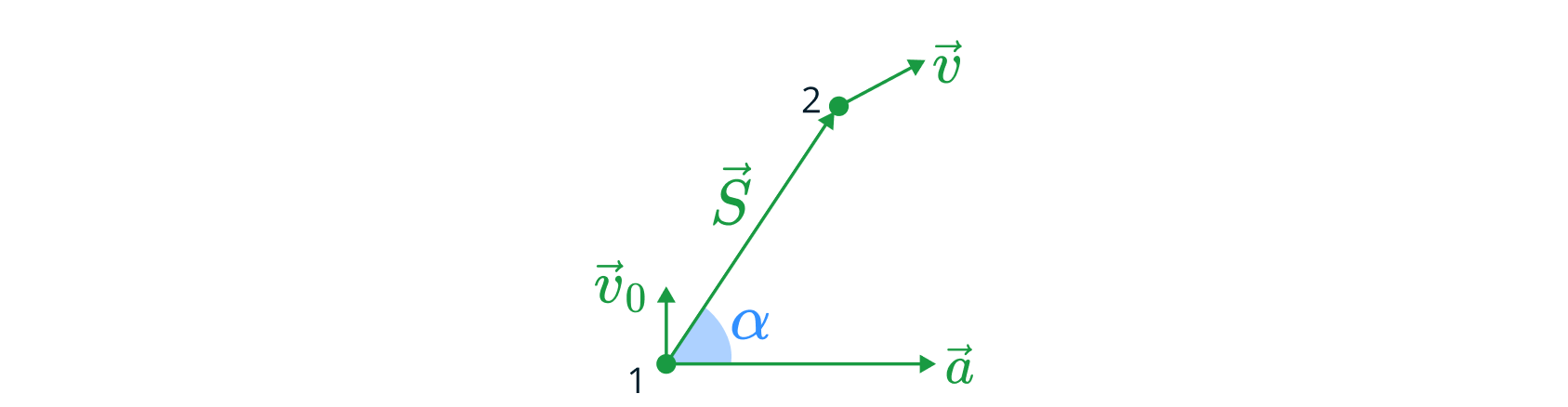
Проекции на ось:

\[ 2 a_x S_x = v_x^2 - v_{0x}^2 \]