Основные формулы

Закон сложения скоростей:

\[ \vec{v}{\text{абс}} = \vec{v}{\text{пер}} + \vec{v}_{\text{отн}} \]

Теория

Пусть существует две системы отсчета (СО): неподвижная \(K\) и подвижная \(K'\), а также тело, которое движется. Введем понятие радиус-вектора.

Радиус-вектор — вектор, выходящий из начала системы координат и направленный к какой-либо точке. Введем вектор \(\vec{l}\), соединяющий начало \(O\) неподвижной СО с началом \(O'\) подвижной СО.

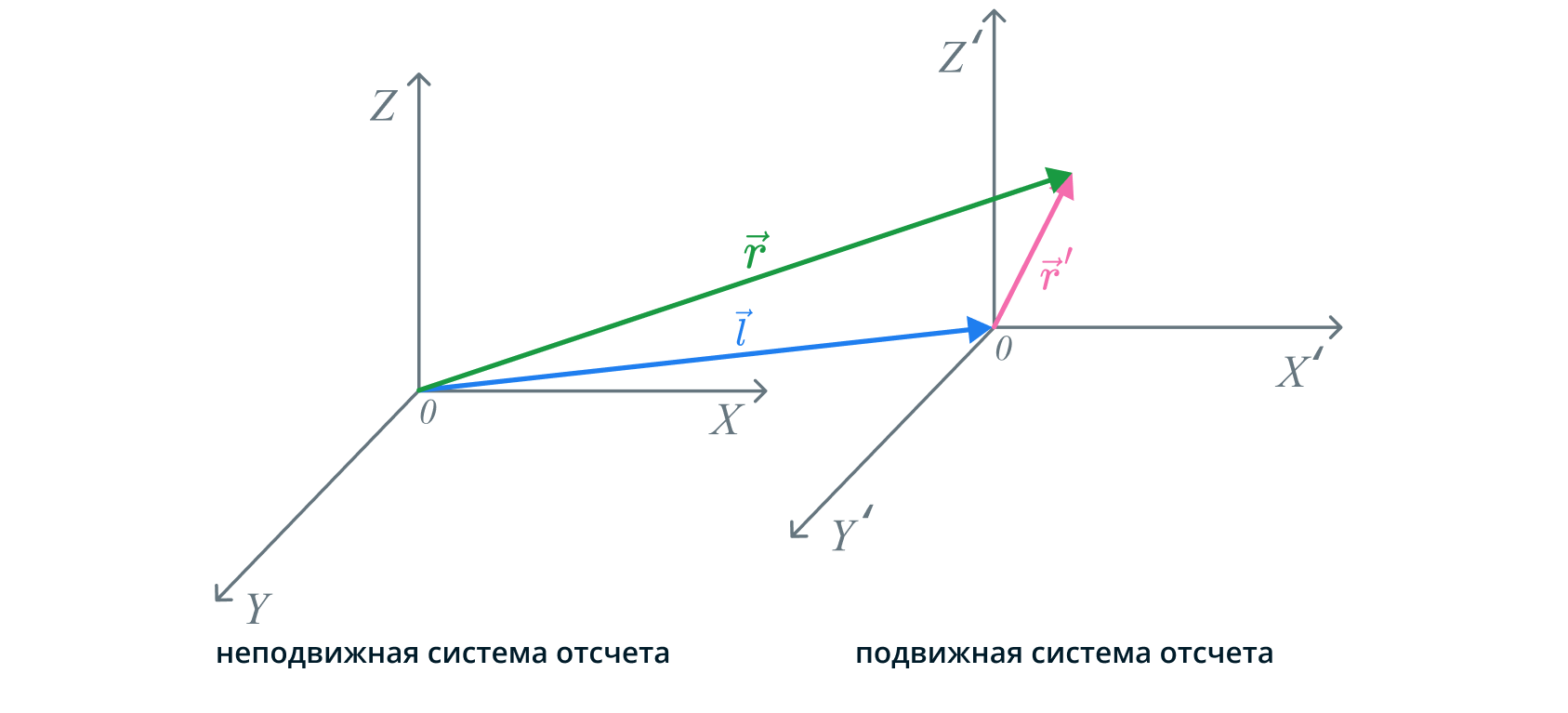
По правилу сложения векторов несложно получить:

\[ \vec{r} = \vec{l} + \vec{r'} \]

Далее учтем, что изменение радиус-вектора — это перемещение, а изменение суммы — это сумма изменений:

\[ \Delta \vec{r} = \Delta (\vec{l} + \vec{r'}) = \Delta \vec{l} + \Delta \vec{r'} \]

Разделим все на \(\Delta t\):

\[ \dfrac{\Delta \vec{r}}{\Delta t} = \dfrac{\Delta \vec{l}}{\Delta t} + \dfrac{\Delta \vec{r'}}{\Delta t} \]

Осталось заметить, что каждая дробь является скоростью по определению. Мы получили закон сложения скоростей:

\[ \vec{v}\text{абс} = \vec{v}\text{пер} + \vec{v}_\text{отн} \]

• Абсолютная скорость \(\vec{v}_\text{абс}\) — скорость тела в неподвижной системе отсчета.

• Переносная скорость \(\vec{v}_\text{пер}\) — скорость подвижной системы отсчета относительно неподвижной.

• Относительная скорость \(\vec{v}_\text{отн}\) — скорость тела в подвижной системе отсчета.

Отсюда можно получить формулу, которая позволяет «пересесть» в нужную систему отсчета:

\[ \vec{v}\text{отн} = \vec{v}\text{абс} + (- \vec{v}_\text{пер}) \]

Таким образом, чтобы перейти в движущуюся систему отсчета, необходимо найти относительную скорость. Для этого от вектора скорости в лабораторной системе отсчета \(\vec{v}\text{абс}\) необходимо вычесть вектор скорости \(\vec{v}\text{пер}\) того тела, в чью систему отсчета мы хотим перейти.

При этом, когда мы переходим в подвижную СО, для нас она мысленно становится неподвижной, так как мы начинаем двигаться вместе с ней.

Стоит отметить, что для того чтобы казаться неподвижной, системе отсчета необходимо обладать большими размерами. Для понимания приведем распространенный пример. В задачах за неподвижную СО часто принимается поверхность Земли, хотя на самом деле сама планета подвижна и движется вокруг Солнца с большой скоростью. Поскольку и наблюдатель, и рассматриваемое в задаче тело находятся на поверхности подвижной Земли, для них эта СО «замораживается» и словно стоит на месте. Поэтому систему отсчета, связанную с поверхностью Земли, часто удобно принять за неподвижную.

Примеры решения задач

Задача 1

Пловец переплывает реку шириной \(L = 400\) м по прямой, перпендикулярной берегу, и возвращается обратно, затратив время \(t_1 = 30\) мин. Проплывая такое же расстояние \(L\) вдоль берега и возвращаясь обратно, затрачивает время \(t_2 = 50\) мин. Во сколько раз скорость пловца превышает скорость реки? * (Задача из сборника ВМК)*

Решение

Введем обозначения: \(v_\text{абс}\) — скорость движения пловца относительно берега, \(v_\text{отн}\) — скорость пловца относительно воды, \(v_\text{пер}\) — скорость течения. Тогда сделаем рисунок для первой ситуации:

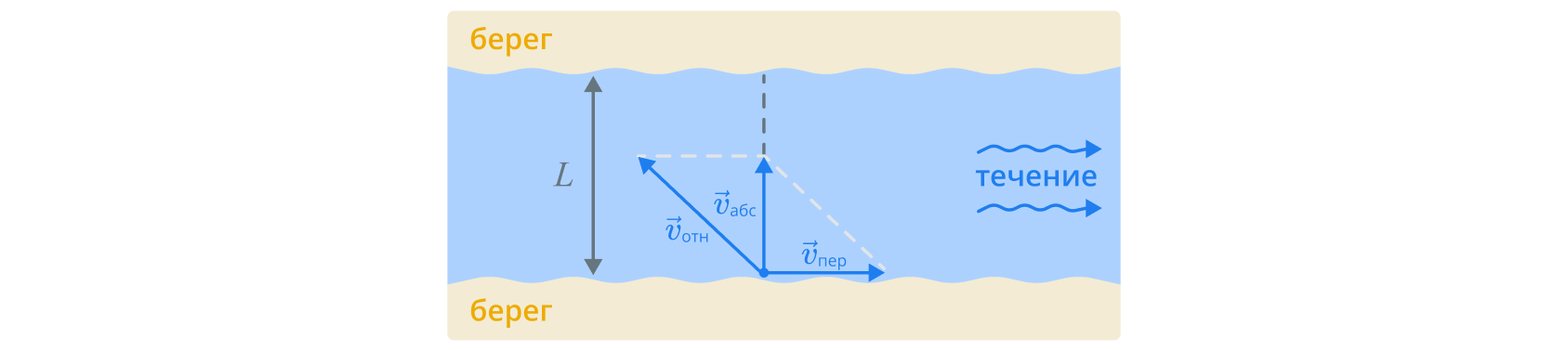
Запишем теорему Пифагора и выразим \(v_\text{абс}\):

\[ v_\text{абс} = \sqrt{v_\text{отн}^2 - v_\text{пер}^2} \]

Время \(t_1\), за которое пловец переплывает берег и возвращается назад:

\[ t_1 = \dfrac{2L}{v_\text{абс}} \]

Подставляя выражение для абсолютной скорости, получим:

\[ t_1 = \dfrac{2L}{\sqrt{v_\text{отн}^2 - v_\text{пер}^2}} \]

Теперь рассмотрим вторую ситуацию: движение вдоль берега. Изобразим движение пловца по направлению течения (\(v_\text{абс} = v_\text{отн} + v_\text{пер}\)) и против течения (\(v_\text{абс} = v_\text{отн} - v_\text{пер}\)).

Время \(t_2\), за которое пловец проплывает вдоль берега расстояние \(L\) туда и обратно:

\[ t_2 = \dfrac{L}{v_\text{отн} + v_\text{пер}} + \dfrac{L}{v_\text{отн} - v_\text{пер}} \]

Возведем формулу для \(t_1\) в квадрат:

\[ t_1^2 = \dfrac{4L^2}{v_\text{отн}^2 - v_\text{пер}^2} \;\; \Rightarrow \;\; v_\text{отн}^2 - v_\text{пер}^2 = \dfrac{4L^2}{t_1^2} \]

Преобразуем формулу для \(t_2\):

\[ \dfrac{2 v_\text{отн} L}{t_2} = v_\text{отн}^2 - v_\text{пер}^2 \]

Приравняем выражения:

\[ \dfrac{4L^2}{t_1^2} = \dfrac{2 v_\text{отн} L}{t_2} \]

Выразим отсюда относительную скорость пловца:

\[ v_\text{отн} = \dfrac{2 L t_2}{t_1^2} \]

Подставим в формулу \(v_\text{отн}^2 - v_\text{пер}^2 = 4L^2 / t_1^2\):

\[ \left(\dfrac{2 L t_2}{t_1^2}\right)^2 - v_\text{пер}^2 = \dfrac{4 L^2}{t_1^2} \]

Выразим скорость реки:

\[ v_\text{пер} = \dfrac{2 L}{t_1^2} \sqrt{t_2^2 - t_1^2} \]

Отношение скоростей:

\[ \dfrac{v_\text{отн}}{v_\text{пер}} = \dfrac{t_2}{\sqrt{t_2^2 - t_1^2}} = \dfrac{50\text{ мин}}{\sqrt{(50\text{ мин})^2 - (30\text{ мин})^2}} = 1,25 \]

Ответ: 1,25

Задача 2

Корабль \(A\) и торпеда \(B\) находятся на расстоянии \(l = 1\) км друг от друга. Скорость корабля \(v_1 = 10\) м/с, угол \(\alpha = 60^\circ\). Скорость торпеды \(v_2 = 20\) м/с. Угол \(\beta\) таков, что торпеда попадёт в цель. * (Задача с олимпиады «Физтех»)*

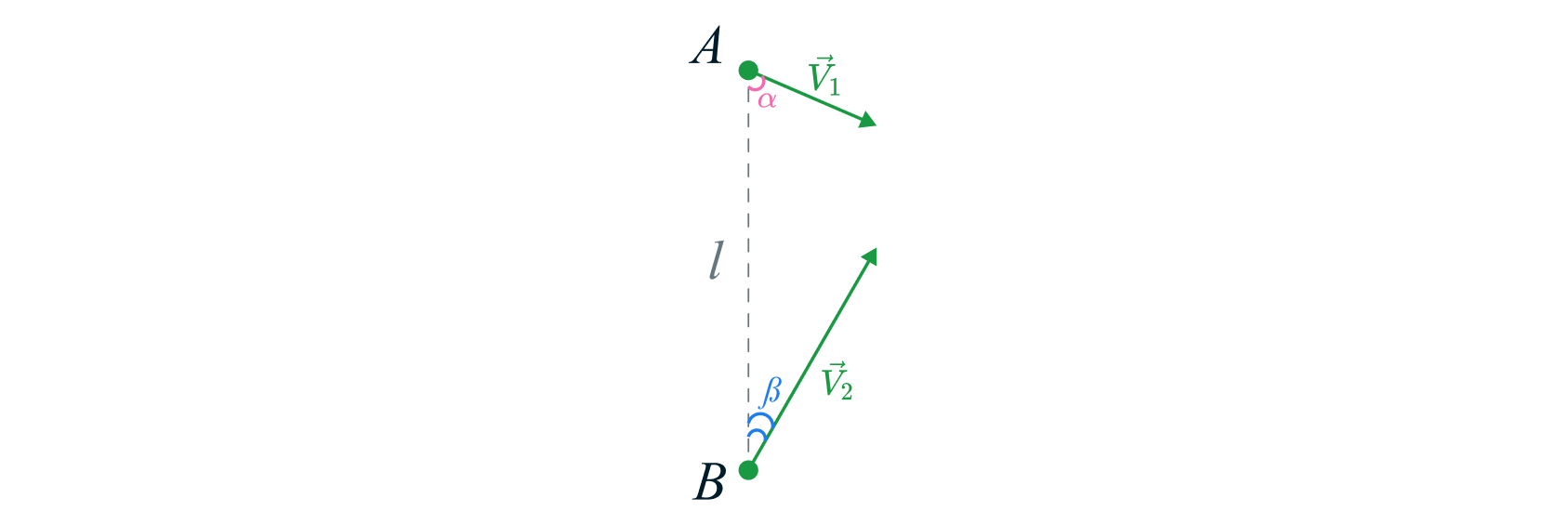
1) Найдите \(\sin \beta\).

2) Через какое время \(T\) расстояние между кораблём и торпедой составит \(S = 770\) м?

Решение

За неподвижную систему отсчета примем воду, а за подвижную систему — корабль \(A\). Отсюда скорость торпеды \(v_2\) — абсолютная скорость, а скорость корабля \(v_1\) — переносная.

Переносим вектор \(\vec{v_1}\) в точку \(B\) противоположно направлению изначального положения, получаем \(-\vec{v_1}\). Введем оси, одну из которых направим по линии \(AB\).

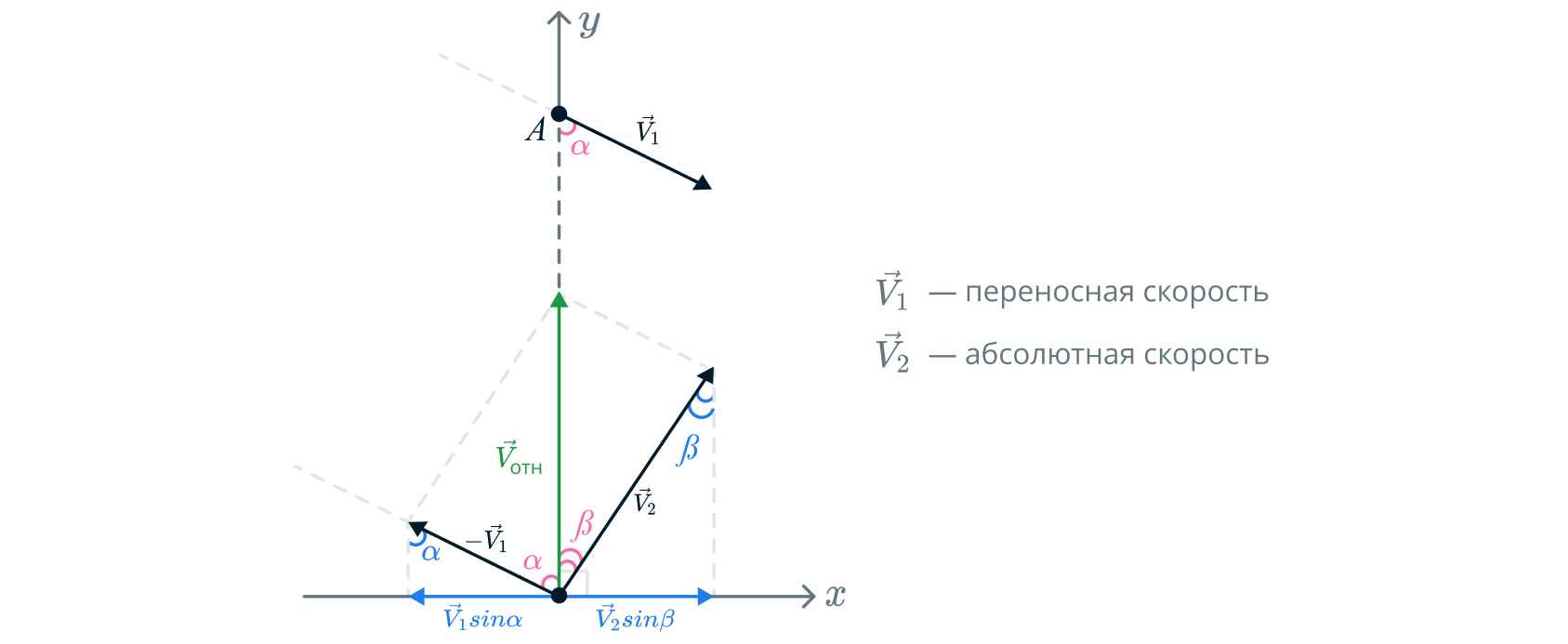
Вектор относительной скорости:

\[ \vec{v}\text{отн} = \vec{v}\text{абс} + (-\vec{v}_\text{пер}) \]

Проекция на ось \(x\):

\[ 0 = v_2 \sin \beta - v_1 \sin \alpha \;\; \Rightarrow \;\; \sin \beta = \sin \alpha \cdot \dfrac{v_1}{v_2} = \dfrac{\sqrt{3}}{4} \]

Проекция на другую ось, ищем время \(T\):

\[ T = \dfrac{l - S}{v_\text{отн}} \]

\[ v_\text{отн} = v_2 \cos \beta + v_1 \cos \alpha \]

\[ T = \dfrac{l - S}{v_2 \cos \beta + v_1 \cos \alpha} \]

\[ \cos \beta = \sqrt{1 - \dfrac{3}{16}} = \dfrac{\sqrt{13}}{4} \]

Подставляем численные значения:

\[ T = \dfrac{1000\text{ м} - 770\text{ м}}{20\;\dfrac{\text{м}}{\text{с}} \cdot \dfrac{\sqrt{13}}{4} + 10\;\dfrac{\text{м}}{\text{с}} \cdot \dfrac{1}{2}} \approx 10 \text{ с} \]

Ответ: 1) \(\dfrac{\sqrt{3}}{4}\); 2) 10 с