Механика

Механические колебания

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Механика

Теоретическая справка

#610

Основные формулы

Зависимость координаты от времени при колебаниях:

x(t)= A cos(ωt+ φ0)

Зависимость скорости от времени при колебаниях:

υ(t)= x′(t)= −A ωsin(ωt+ φ0)

Зависимость ускорения от времени при колебаниях:

a(t) =υ′(t)= − Aω2cos(ωt+ φ0)

Потенциальная энергия при гармонических колебаниях:

m ω2x2 Eпот =---2--

Полная энергия при гармонических колебаниях:

2 2 E = m-ω-A- 2

Максимальная скорость:

υmax = Aω

Максимальное ускорение:

amax =A ω2

Связь циклической частоты и «обычной»:

ω = 2πν

Период колебаний и частота:

T = 1 ν

Период математического маятника:

∘ -- T = 2π l g

Период пружинного маятника:

∘ m-- T = 2π k-

Длина волны:

υ- λ = υT = ν

Основные понятия

Понятие механических колебаний

Механические колебания — это движение, повторяющееся в пространстве и во времени точно или почти точно.

Для того, чтобы система тел могла находится в состоянии механических колебаний (совершать колебательное движение), необходимы следующие условия:

наличие в системе силы, стремящейся вернуть её в положение равновесия,
влияние внутренних сил трения и сопротивления на систему пренебрежимо мало.

Понятие периода и частоты механических колебаний

Период колебаний — это время, за которое система совершает одно полное колебание. Полное колебание означает, что система, дважды пройдя положение равновесия, возвращается в начальное положение.

Единицы измерения: $[T]=$ c (секунда).

Частота колебаний — это величина, обратная периоду. Частота показывает, сколько полных колебаний совершается в единицу времени.

Единицы измерения: $[ν]=$ об/с (обороты в секунду) $=$ c $−1 =$ Гц (Герц)

Гармонические колебания

Гармонические колебания — это механические колебания, при которых координата зависит от времени по гармоническому закону (по закону синуса или косинуса):

x(t)= A cos(ωt+ φ0)

Поговорим о физическом смысле коэффициентов $A$ , $ω$ .

$A$ определяется как амплитуда колебаний — это величина наибольшего отклонения системы от положения равновесия.
Единицы измерения: $[A]=$ м (метр).
Величина $ω$ определяется как циклическая частота — это число колебаний за $(2π)−1$ секунд:

$N- 2π- ω = 2πt = 2πν = T$

Единицы измерения: $[ω]=$ рад/с (радиан в секунду).
Аргумент косинуса $ωt+ φ0 = φ$ называется фазой колебаний, а величина $φ0$ , равная значению фазы при $t= 0$ , называется начальной фазой. Причем для начальной координаты тела имеем:

$x0 = A cosφ0$

Единицы измерения: $[φ]=$ рад (радиан).

Динамика гармонических колебаний

Найдем дифференциальное уравнение, решение которого соответствует зависимости координаты от времени $x(t)$ при гармонических колебаниях. Для этого вычислим производные функции $x(t)$ по времени.

Первая производная по времени:

x′ = − Aωsin(ωt+ φ0)

Вторая производная по времени:

x′′ = −Aω2cos(ωt+φ0) =− ω2x

Из сравнения полученных выражений следует основное уравнение динамики гармонических колебаний:

′′ 2 x + ω x= 0

Решением этого уравнения всегда будет функция вида:

x= A cos(ωt+ φ0)

Понятие свободных колебаний. Пружинный и математический маятники

Свободные колебания — колебания, вызванные внутренними силами системы (силами, с которыми тела системы взаимодействуют друг с другом).

Рассмотрим пример простейшей колебательной системы (осциллятора), совершающей свободные колебания — пружинный маятник.

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

$PIC$

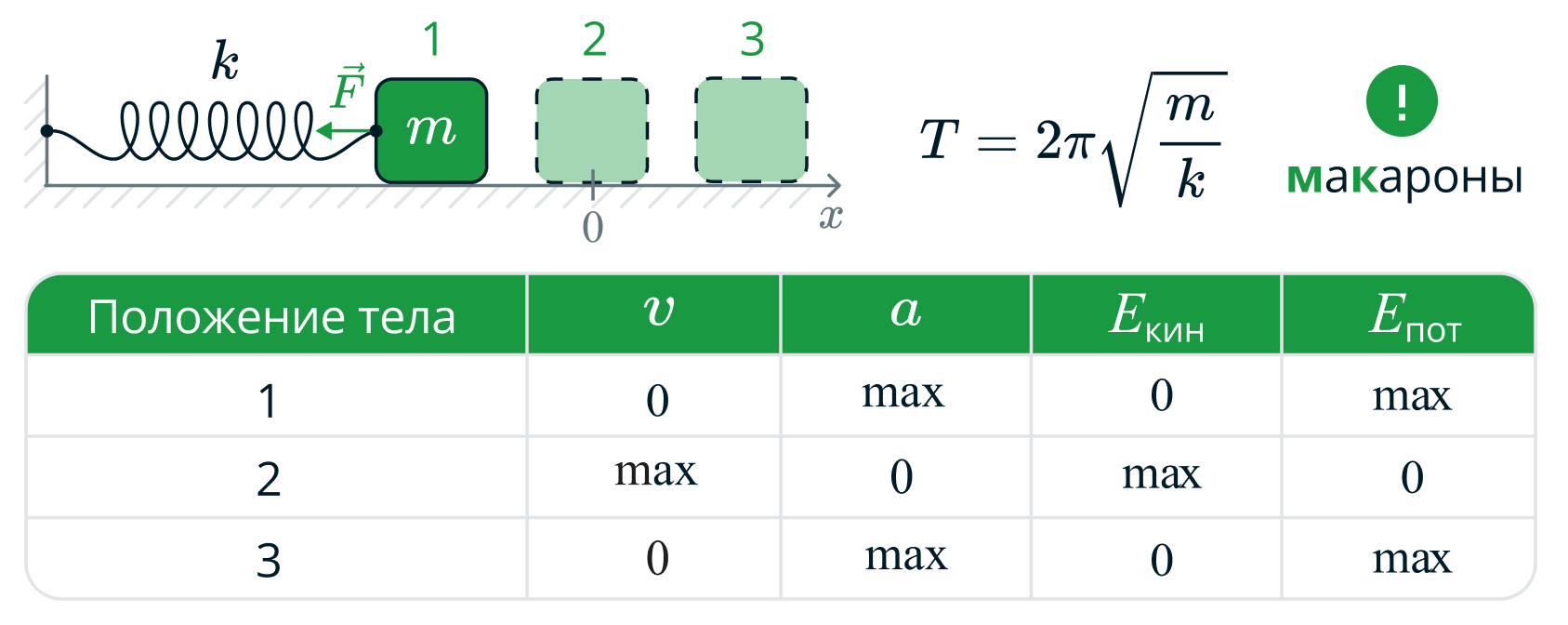
Будем считать, что пружинный маятник совершает малые горизонтальные колебания. Будем называть колебания малыми, если при них величина деформации пружины много меньше её размеров. Такое рассмотрение позволит нам воспользоваться законом Гука. Трением пренебрегаем. Пользуясь такой моделью, найдем период колебаний пружинного маятника.

Груз имеет массу $m$ , жёсткость пружины равна $k$ . Координате $x = 0$ отвечает положение равновесия, в котором пружина не деформирована. Величина деформации пружины равна модулю координаты груза. В горизонтальном направлении на груз действует только сила упругости $⃗F$ со стороны пружины. Второй закон Ньютона для груза в проекции на ось $x$ имеет вид:

max = − kx

Если $x >0$ (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону и $Fx < 0$ . Наоборот, если $x< 0$ , то $Fx > 0$ . Знаки $x$ и $Fx$ всё время противоположны, поэтому закон Гука можно записать так:

F = −kx x

Учитывая второй закон Ньютона:

max+ kx =0

Приведем полученное соотношение к виду, отвечающему основному уравнению динамики гармонических колебаний:

( ) ∘ k--2 ax+ m- ⋅x = 0

Отсюда можем написать выражение для квадрата циклической частоты:

ω2 =-k m

Из соотношения $T = 2π∕ω$ находим период горизонтальных колебаний пружинного маятника.

∘ --- T = 2π m- k

Математический маятник — это колебательная система, представленная материальной точкой, подвешенной на невесомой нерастяжимой нити или легком стержне. Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

$PIC$

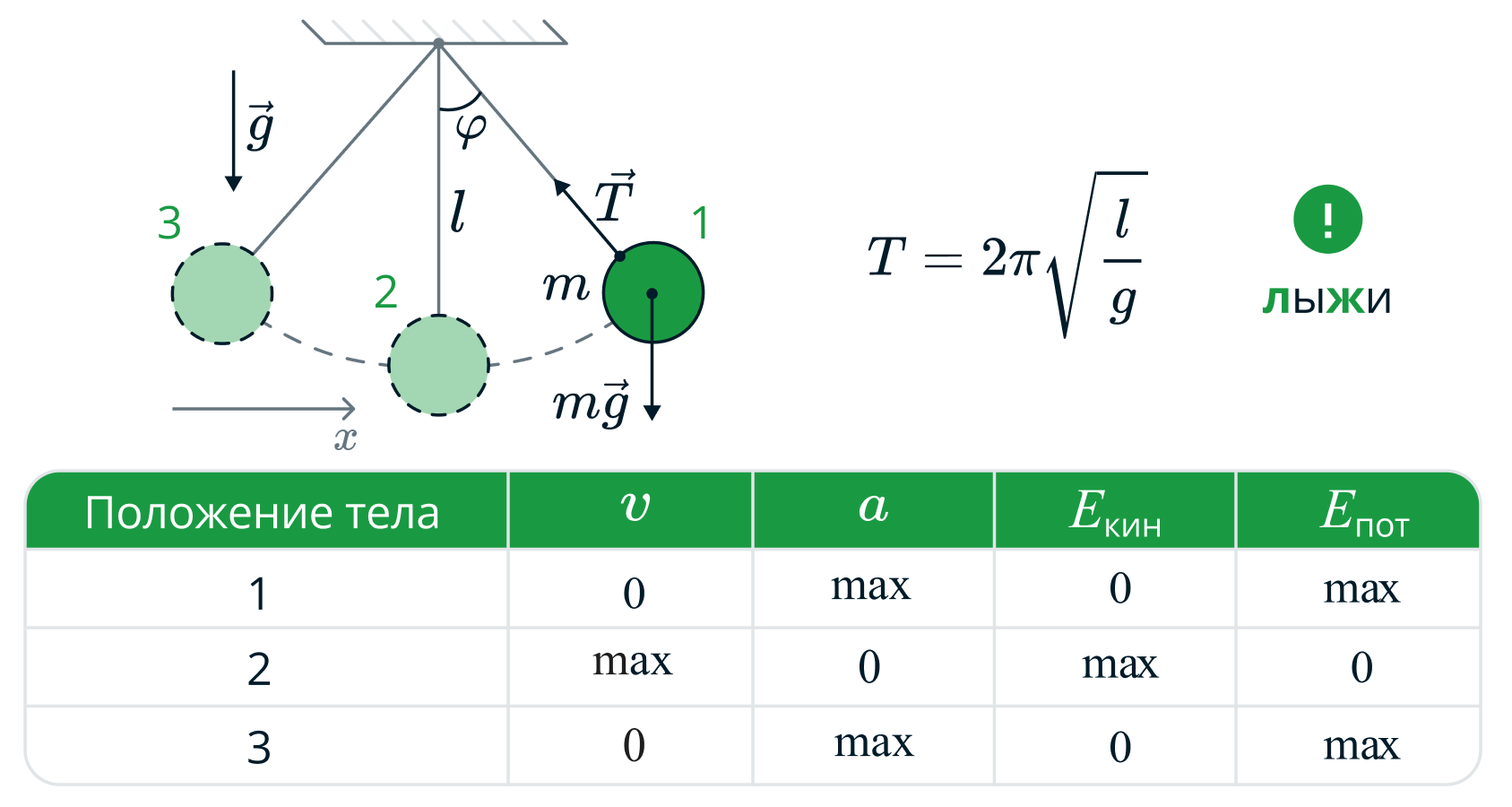
Пусть длина нити равна $l$ , координате $x =0$ соответствует положение равновесия, сопротивлением воздуха пренебрегаем. Найдём период малых колебаний математического маятника. Запишем для маятника второй закон Ньютона:

m⃗a =m ⃗g+ ⃗T

и спроектируем его на ось $x$ :

max = Tx

Если маятник занимает положение 1 ( $x >0$ ), то

Tx = −T sinφ = −Tx l

Если же маятник находится по другую сторону от положения равновесия (т.е. $x <0$ ), то:

x Tx = T sinφ = −T l

Итак, при любом положении маятника имеем

max = −T x l

Когда маятник покоится в положении равновесия, выполнено равенство $T = mg$ . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство $T ≈ mg$ . Воспользуемся им в предыдущей формуле:

max = −mg x ⇒ ax = −gx ⇒ ax +x g= 0 l l l

Это уравнение гармонических колебаний, в котором $g∕l$ называют квадратом циклической частоты:

ω2 = g l

Отсюда и из соотношения $T = 2π∕ω$ находим период математического маятника

∘ -- T = 2π l g

Энергия и её превращения при гармонических колебаниях

Кинетическая энергия гармонических колебаний

Кинетическая энергия для произвольной механической системы определяется выражением: $Eкин = mv2∕2$ . Нам уже удалось получить выражение для зависимости скорости от времени при гармонических колебаниях, подставим его в формулу для кинетической энергии:

2 2 Eкин = mA-ω-sin2(ωt+ φ0) 2

Видно, что кинетическая энергия при гармонических колебаниях изменяется по закону квадрата синуса.

Потенциальная энергия гармонических колебаний

В общем случае, потенциальная энергия гармонических колебаний определяется выражением:

m ω2x2 Eпот =---2--

Например, для потенциальной энергии деформированной пружины имеем выражение:

2 E пот = kx-, 2

где $ω2 = k∕m$ - уже известное нам соотношение для пружинного маятника.

Подставим в формулу для потенциальной энергии гармонических колебаний выражение для координаты $x(t)$ :

2 2 Eпот = mA-ω--cos2(ωt+ φ0) 2

По аналогии с кинетической энергией, потенциальная изменяется по закону квадрата косинуса. Обратите внимание на то, что кинетическая и потенциальная энергии изменяются в противофазе. Максимальному значению потенциальной энергии соответствует минимальное значение кинетической и наоборот. При этом период изменения энергии при гармонических колебаниях в 2 раза меньше периода колебаний $x,$ $v,$ $a$ :

$PIC$

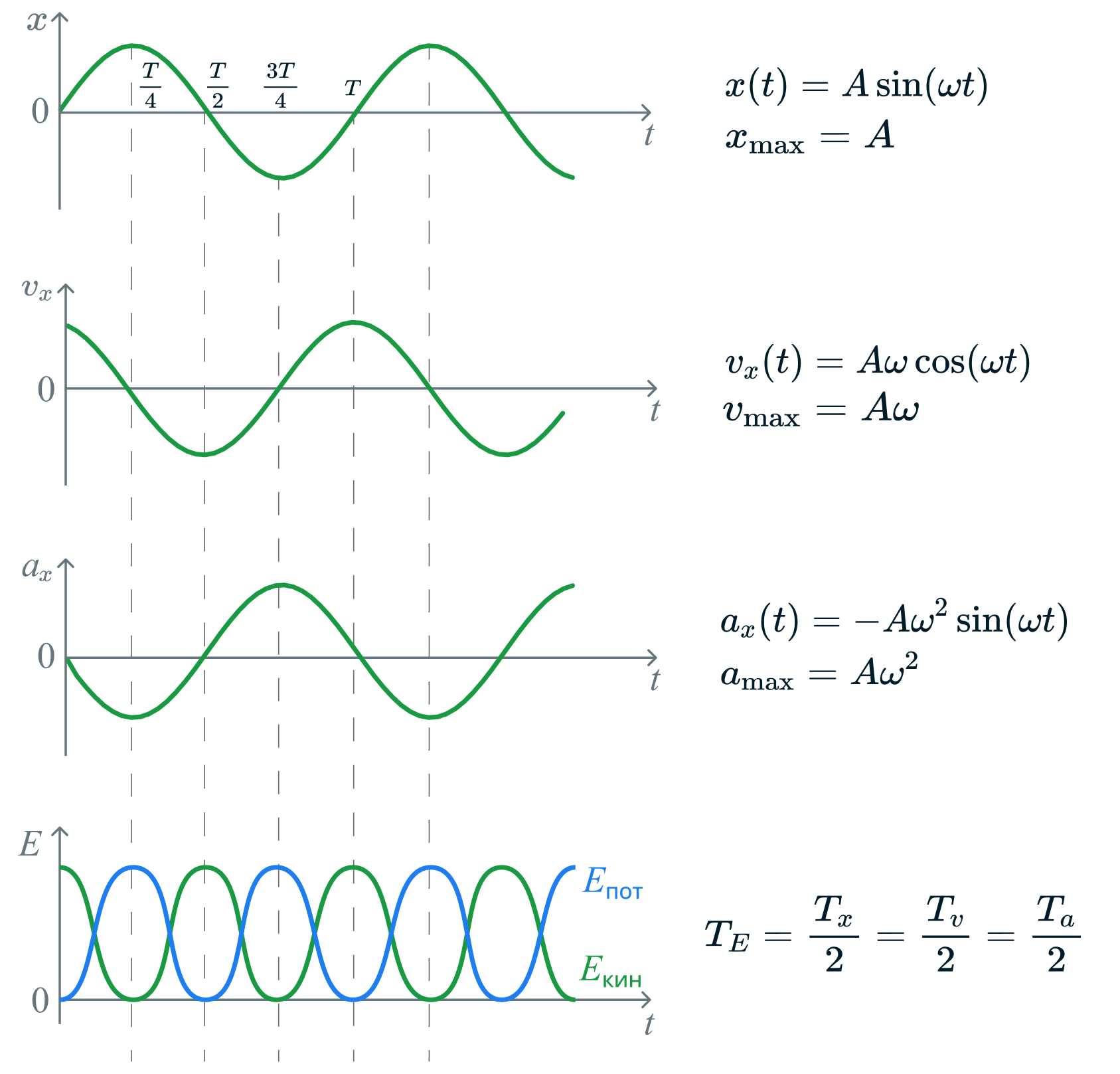
Полная энергия гармонических колебаний

Полная энергия системы определяется суммой кинетической и потенциальной энергий. Вспомним основное тригонометрическое тождество и получим выражение для полной энергии $E$ при гармонических колебаниях.

2 2 2 2 E = mA-ω-(sin2(ωt+ φ0)+cos2(ωt+ φ0))= mA--ω-. 2 2

Предыдущая справка

Следующая справка