Конденсаторы
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#616
Элементы электростатики
Рассмотрим бесконечную равномерно заряженную пластину. Пусть пластина заряжена положительно. Данная
бесконечная равномерно заряженная пластина создает вокруг себя однородное электрическое поле и
напряженность . Электрическое поле принято направлять от «плюса» к «минусу», покажем это на
рисунке.
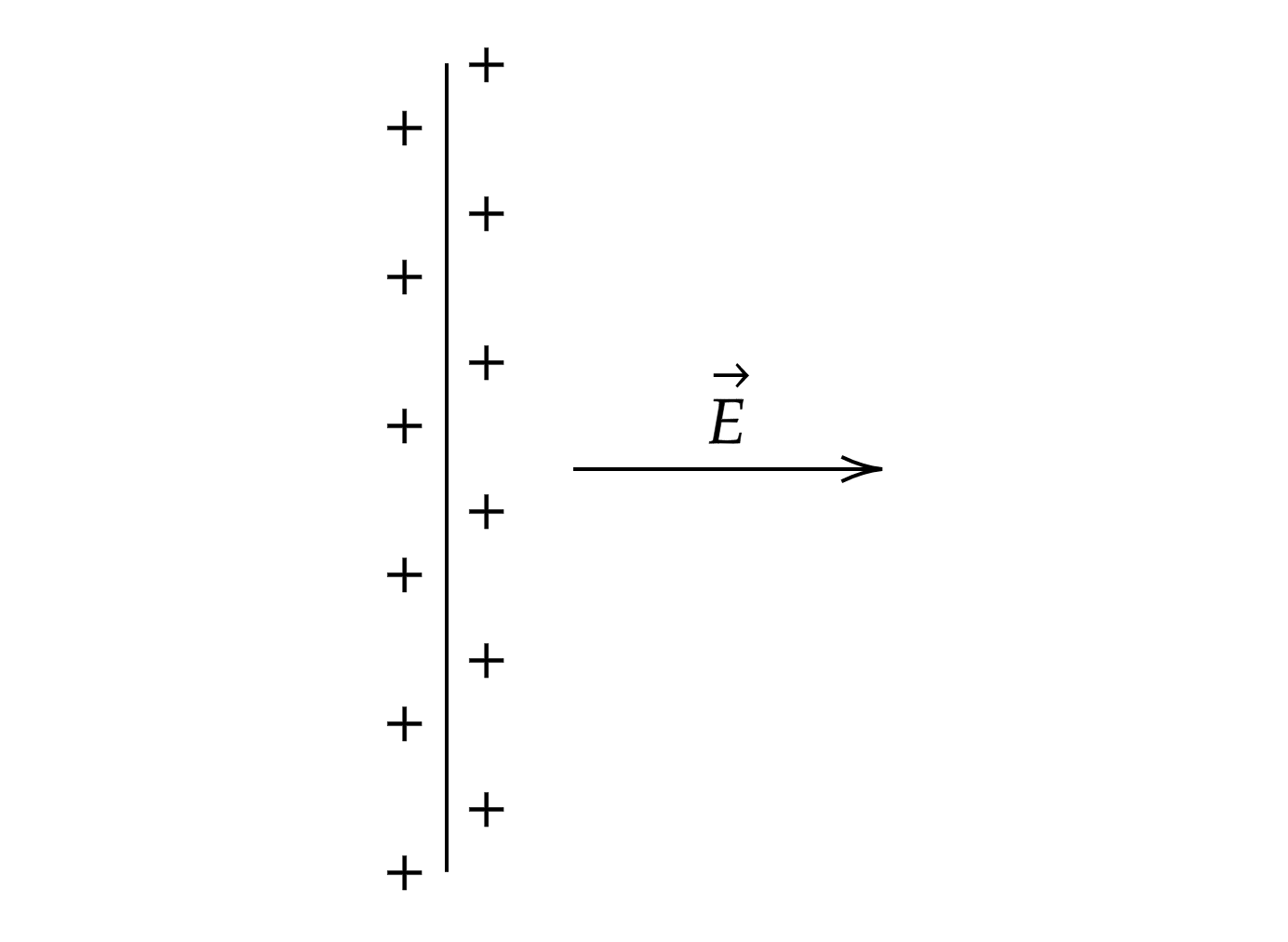
Для напряженности, создаваемой бесконечной равномерно заряженной пластиной, справедливо:
Буквой обозначена диэлектрическая проницаемость среды диэлектрика. Вокруг данной пластины может быть
диэлектрик, и величина
показывает, во сколько раз уменьшается электрическое поле в диэлектрике. Поверхностная
плотность заряда
— отношение малого заряда
к малой площади
, по которой он равномерно
распределен:
Итак, бесконечная равномерно заряженная пластина создает вокруг себя электрическое поле, и в каждой точке оно одинаково. Из последней формулы можно сделать вывод, что в данном случае электрическое поле является однородным и не зависит от расстояния.
Плоский конденсатор
Теперь рассмотрим систему из двух таких пластин, причем одну равномерно зарядим положительно, а вторую — отрицательно. Пусть расстояние между пластинами очень мало по сравнению с их длиной, тогда мы можем рассматривать эти пластины как бесконечные равномерно заряженные (то есть как модель, описанную выше).
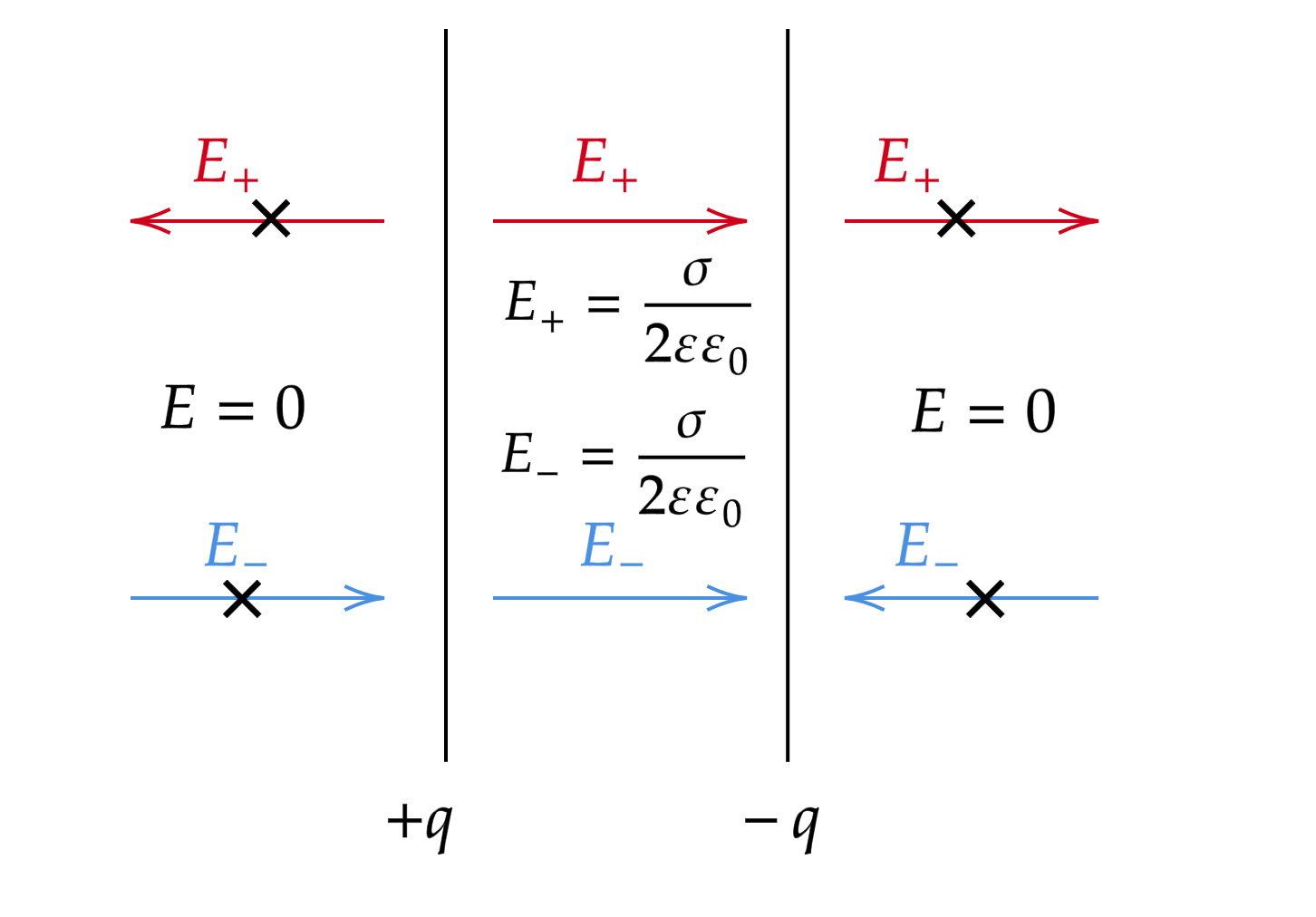
Пластина с положительным зарядом создает напряженность, направленную «от себя», а пластина с
отрицательным зарядом
создает напряженность, направленную «к себе». Заряды
и
равны по модулю.
Пусть площадь пластин одинакова. Из этих двух фактов следует, что поверхностная плотность заряда на пластинах
также одинакова. Следовательно, рассматриваемые пластины создают одинаковые напряженности и одинаковое
электрическое поле вокруг себя.
По бокам системы электрические поля взаимно уничтожают друг друга, то есть суммарное поле снаружи системы пластин равно нулю. Внутри же векторы напряженности сонаправлены, поэтому электрические поля суммируются.
Рассмотренная система пластин имеет свое название и очень часто встречается в задачах.
Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.
Электрическая емкость
Конденсатор предназначен для накопления заряда и энергии электрического поля и обладает емкостью. Введем для рассмотренной ранее системы из двух пластин понятие электрической емкости.
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение
заряда (по модулю) одного из проводников к разности потенциалов
между ними:
Единицы измерения:
фарад.
Эта формула дается электроемкости по определению. Ее можно объяснить, основываясь на принципах электростатики. Если на проводник помещают некоторый заряд, то на всем проводнике потенциал одинаковый — это свойство проводника. При увеличении заряда, помещаемого на проводник, потенциал увеличивается, то есть можно сказать, что потенциал прямо пропорционален помещенному на проводник заряду. Для данной зависимости коэффициентом пропорциональности является электроемкость.
Электроемкость плоского конденсатора
Поле конденсатора суммируется из двух полей, создаваемых каждой пластиной в отдельности. Примем, что каждая из пластин имеет одинаковую площадь и заряд, поэтому они создают одинаковую напряженность:
Распишем поверхностную плотность заряда по определению
Поле внутри конденсатора можно считать однородным, поэтому в данном случае справедливо, что
Приравняем напряженности конденсатора:
Из определения электроемкости имеем, что . С учетом этого запишем предыдущее выражение:
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и
обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком,
электроемкость конденсатора увеличивается в раз:
где — расстояние между пластинами,
— площадь пластины,
— диэлектрическая проницаемость,
—
электрическая постоянная.
Конденсаторы в электрической цепи
Пусть конденсатор емкостью подключен к источнику, ЭДС которого равна
. Полное электрическое
сопротивление цепи обозначим
. В цепи идет электрический ток
, благодаря которому на обкладках конденсатора
будет накапливаться электрический заряд.
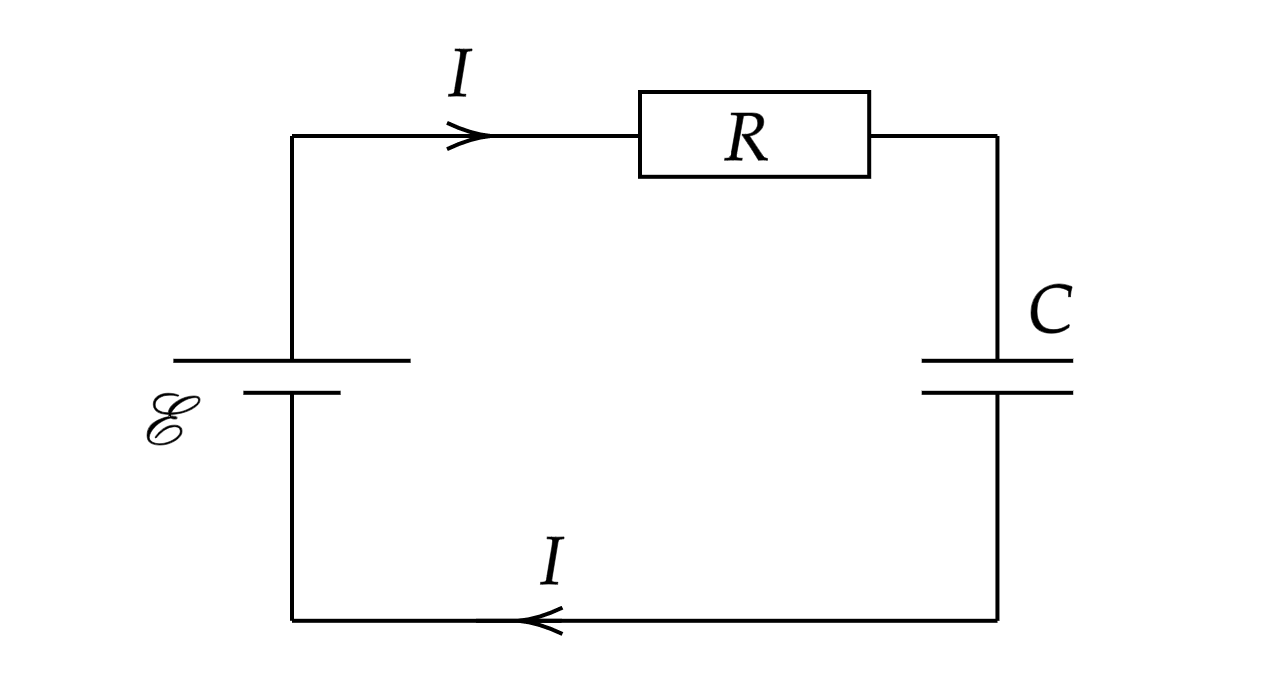
Исходя из того, что элементы в цепи соединены последовательно, сумма напряжений на конденсаторе и на
резисторе
равна ЭДС источника
Проанализируем полученную формулу с точки зрения рассматриваемой цепи.
При изначально замкнутой электрической цепи заряд на конденсаторе равен нулю, следовательно, напряжение на нем отсутствует и сила тока равна:
В процессе зарядки конденсатора заряд на нем увеличивается, следовательно, сила тока уменьшается. В конечный момент времени конденсатор может полностью зарядиться:
Обратите внимание, что эти рассуждения и формулы верны только для конкретной, рассматриваемой нами цепи. В других случаях эти формулы могут не работать. Теперь докажем важный факт, который верен всегда.
Установившийся режим цепи — состояние, при котором все параметры электрической цепи остаются неизменными с
течением времени. Чтобы выполнились эти условия, заряд на конденсаторе также должен быть постоянным
.
Сила тока, протекающего через конденсатор — изменение заряда на конденсаторе с течением времени:
При установившемся режиме заряд на конденсаторе не должен меняться. Следовательно, при установившемся режиме сила тока через конденсатор равна нулю:
При установившемся режиме ток через конденсатор не идет.
В задаче говорится именно об установившемся режиме, если:
- в условии это конкретно прописано;
- есть фраза «через длительный промежуток времени» или подобная;
- не дано описание какого-либо состояния в принципе.
Как правило, в задачах ЕГЭ всегда подразумевается, что мы должны рассчитать установившийся режим цепи.
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно.
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин.

Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
Сократив выражение на , получим формулу:
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
Параллельное соединение конденсаторов
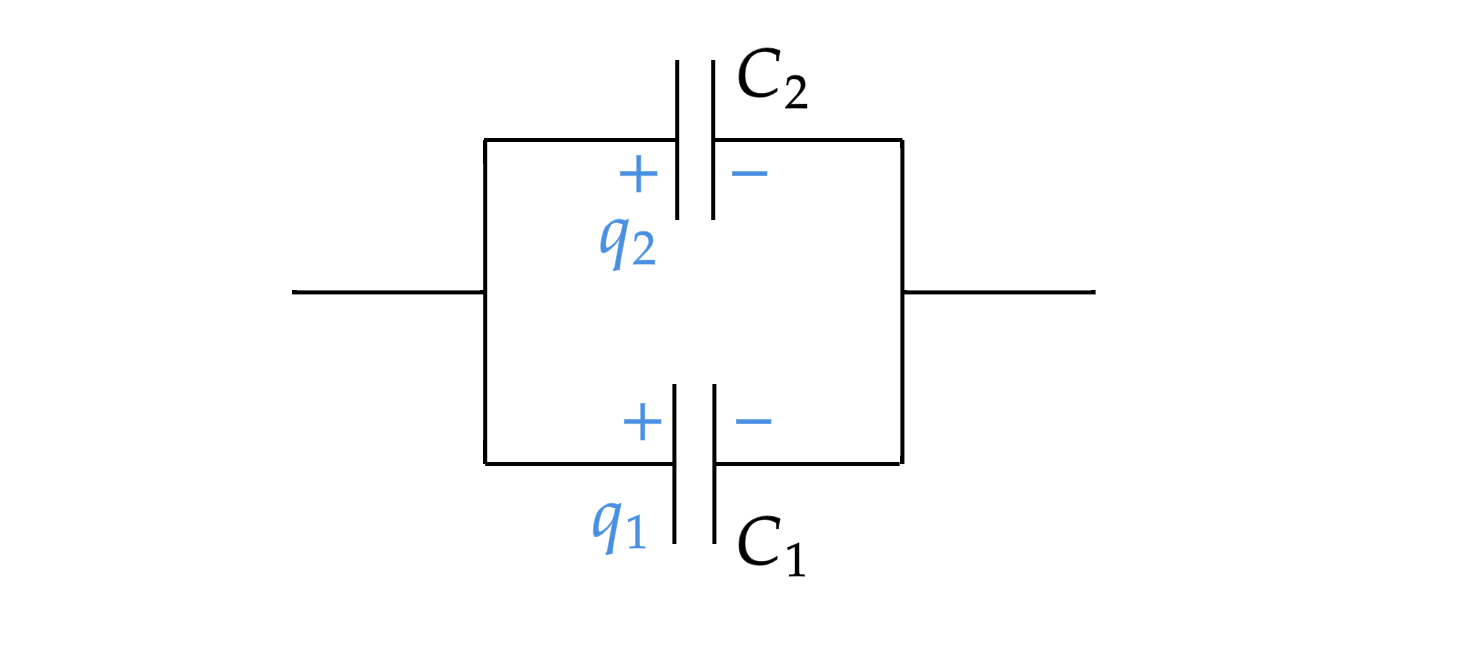
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
Так как заряд конденсатора
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
Расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. Вычислим эту энергию на примере плоского воздушного конденсатора.
Каждая из пластин создает свое электрическое поле. Так как пластины заряжены разноименно, то они
притягиваются друг к другу посредством электрической силы . Приложим против электрической силы некоторую
силу
и отставим пластины на расстояние
друг от друга.
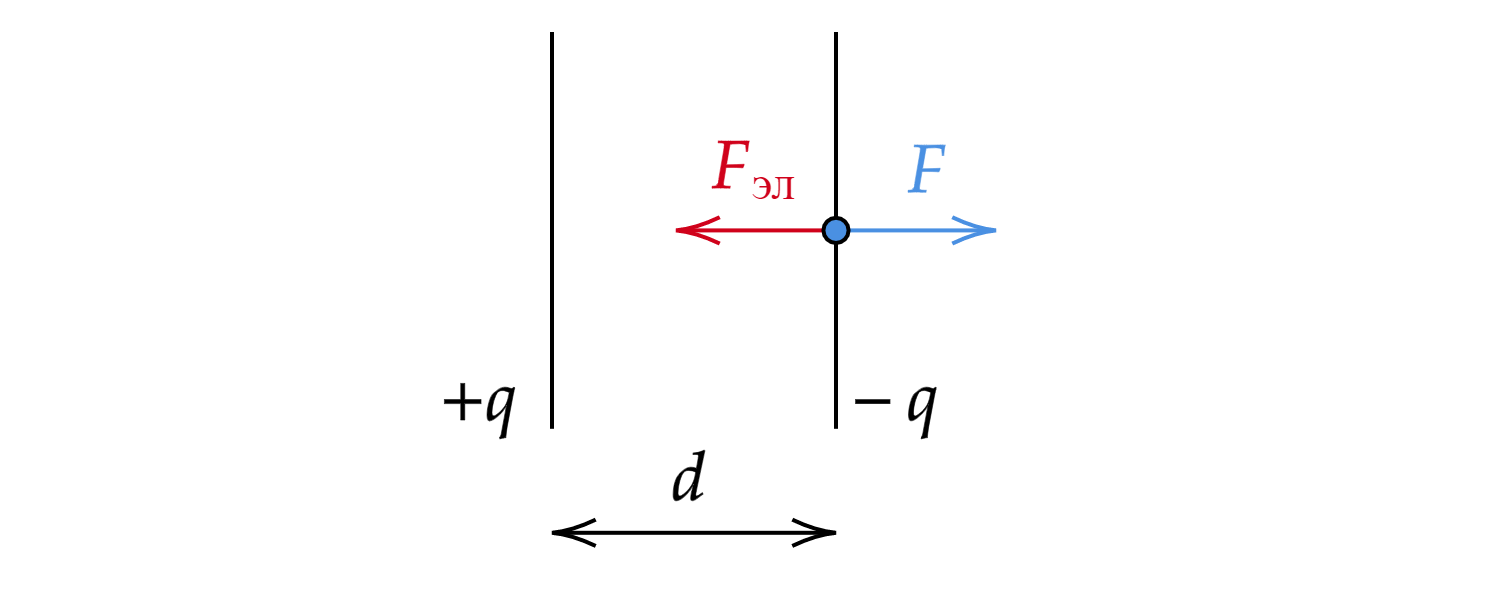
При разъединении пластин совершалась работа, которая равна
Электрическое поле конденсатора не зависит от емкости, а также от расстояния между его пластинами:
Следовательно, сила является постоянной и равна электрической силе по модулю:
В свою очередь сила электрическая характеризует взаимодействие одной пластины с электрическим полем второй:
где — энергия конденсатора.
Почему? Поле внутри конденсатора создается с помощью двух электрических полей от каждой пластины по
отдельности . Рассмотрим пластину с зарядом
(аналогично можно было рассмотреть пластину с
положительным зарядом). Пластина с зарядом
взаимодействует только с электрическим полем, создаваемым
пластиной с зарядом
, она не может взаимодействовать со своим же зарядом. Сила электрического
взаимодействия двух пластин конденсатора есть произведение заряда одной пластины (по модулю) и электрического
поля, создаваемого второй пластиной:
Вернемся к формуле работы, совершаемой при разъединении пластин, и учтем, что :
С учетом того, что емкость конденсатора , получаем еще две формулы для энергии:
Эти три формулы универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
Закон изменения энергии в электрической цепи
Сумма работ источника тока и механических сил равна сумме изменения энергии в цепи и количества теплоты, выделяемого в цепи.
Энергия в электрической цепи запасается в двух видах электрических элементов — в конденсаторе или/и в катушке индуктивности. То есть энергия электрической цепи — это суммарная энергия всех конденсаторов и катушек индуктивности.
1.Энергия, запасаемая в конденсаторе:
где — емкость конденсатора,
— напряжение на конденсаторе,
— заряд конденсатора.
Энергия, запасаемая в катушке индуктивности:
где — индуктивности катушки,
— сила тока, протекающего через катушку, Ф — магнитный поток, ее
пронизывающий.
2. Формула для работы источника вытекает из понятия ЭДС:
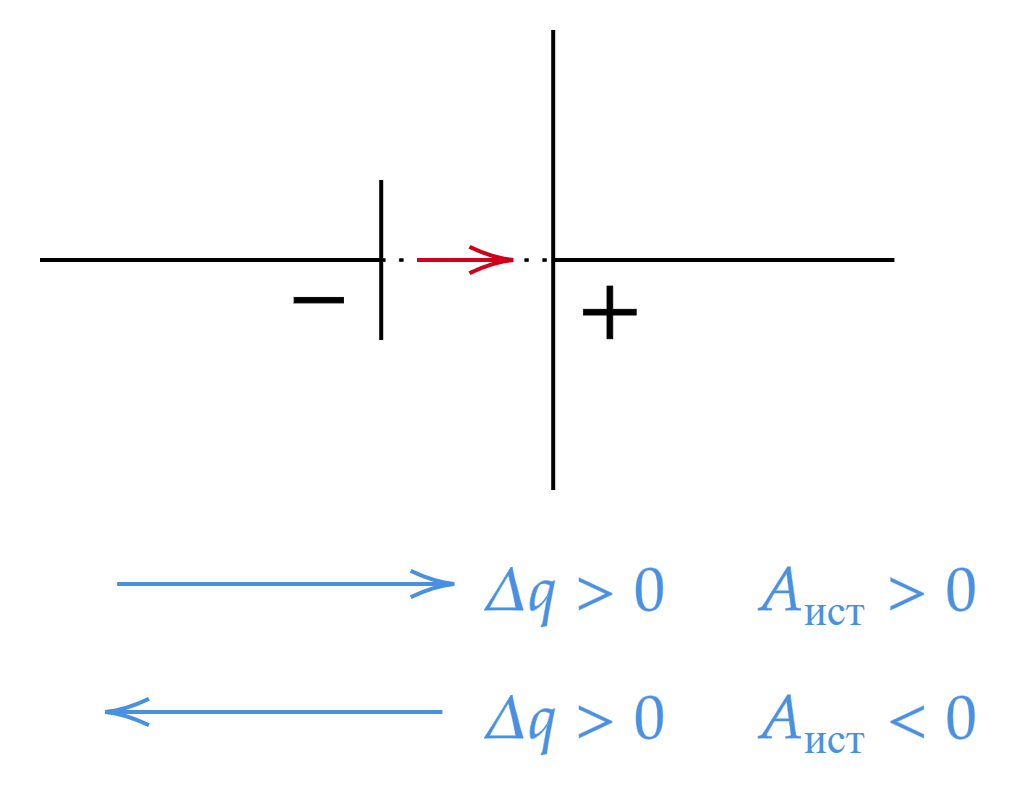
Если положительный заряд протекал по направлению действия сторонних сил этого источника, то источник совершил положительную работу
Если положительный заряд протекал по направлению, противоположному действию сторонних сил этого источника, то источник совершил отрицательную работу
Тепловая мощность при различных соединениях резисторов
Здесь рассматривается тепловая мощность, выделяемая за равные промежутки времени.
Последовательное соединение резисторов
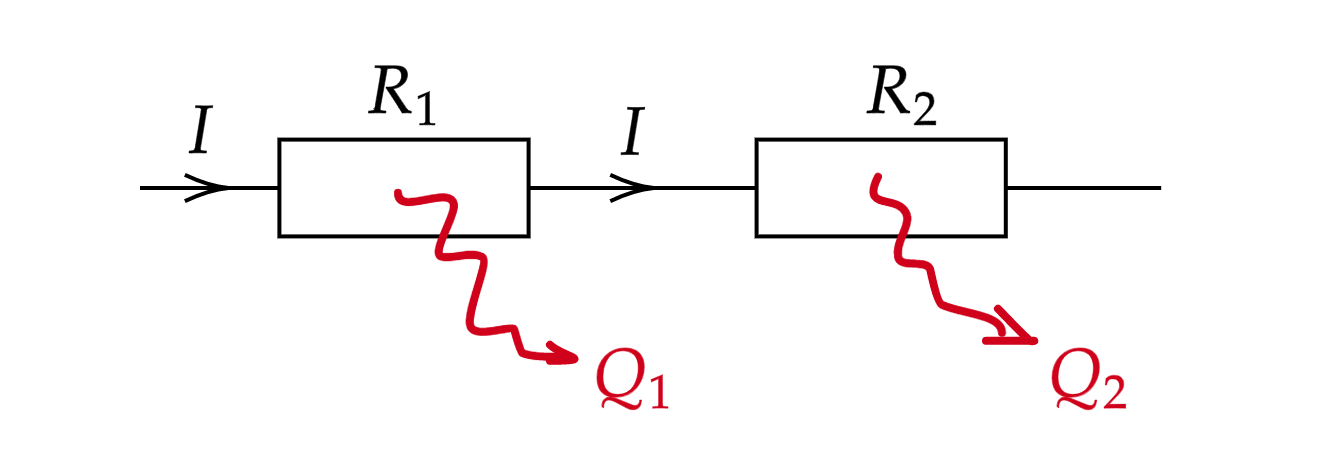
При последовательном соединении через резисторы протекает одинаковая сила тока.
Исходя из формулы для мощности , можем получить следующие соотношения:
Тепловая мощность прямо пропорциональна сопротивлениям.
Параллельное соединение резисторов
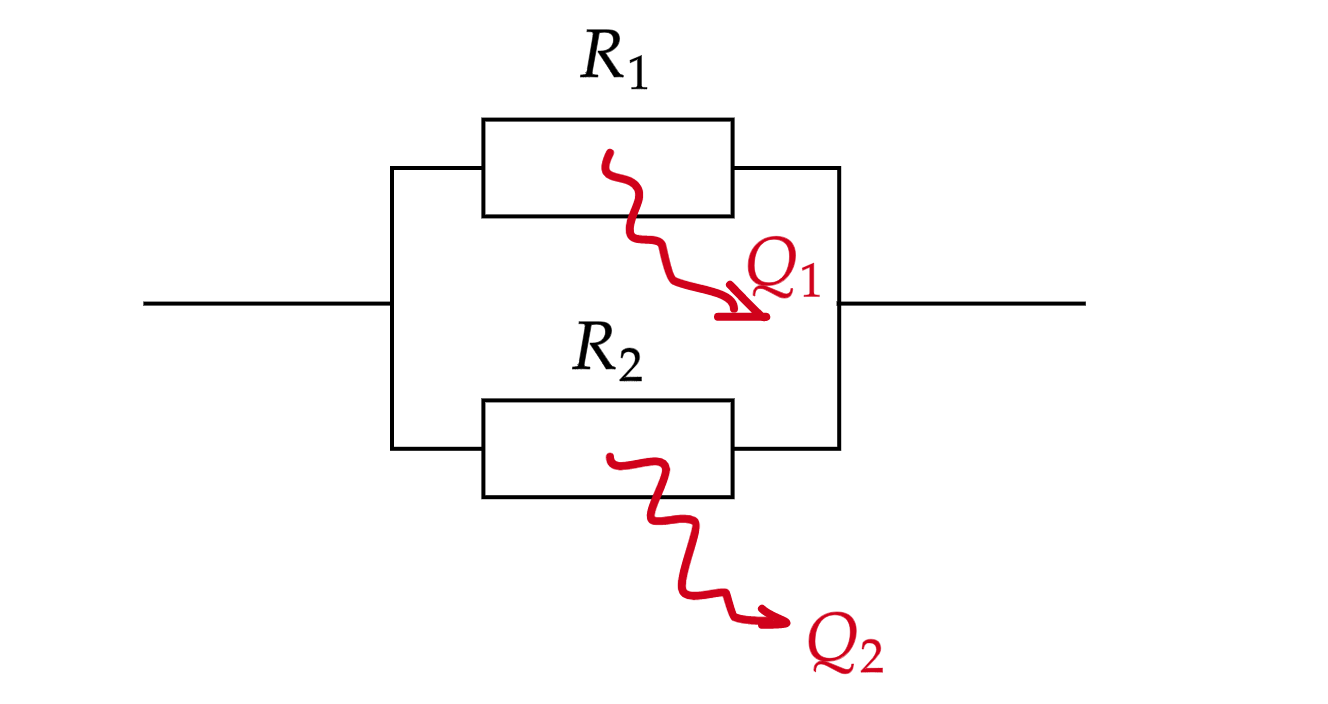
При параллельном соединении резисторов напряжение на них одинаково.
Исходя из формулы для мощности , можем получить следующие соотношения:
Тепловая мощность обратно пропорциональна сопротивлениям.
Общее количество теплоты:
