Катушка индуктивности
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#617
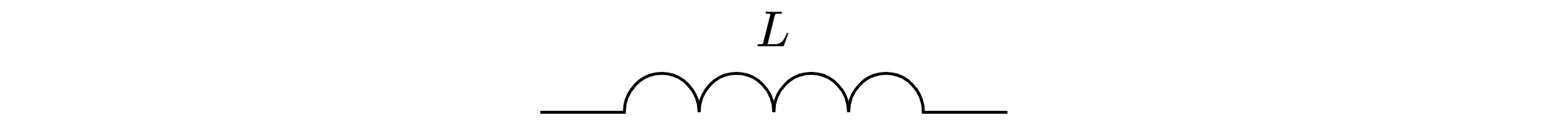
Пусть существует катушка индуктивности, обладающая индуктивностью . В катушке индуктивности возникает
ЭДС самоиндукции, определяющаяся по формуле:
Или упрощенно:
Напряжение в катушке индуктивности определяется выражением:
Ключевые свойства катушки индуктивности
- Ток не меняется скачком
Поскольку в катушке индуктивности напряжение определяется приведенной выше формулой, то сила протекающего в
ней тока не может резко меняться.
- При установившемся режиме сила тока в катушке постоянна
Таким образом, при установившемся режиме идеальную катушку индуктивности можно рассматривать как
провод.
- Энергия, запасенная в катушке индуктивности:
Пример №1
Разберем стандартную конструкцию — электрическую цепь, состоящую из источника и последовательно
подключенных резистора
и катушки индуктивности
.

Проанализируем зависимость силы тока от времени
и построим ее график.
Шаг 1: ключ разомкнут. В начальный момент времени (до замыкания ключа) сила тока на катушке индуктивности и в целом в цепи равна нулю.
Шаг 2: ключ только что замкнули. Замкнем ключ — начальная сила тока в цепи равна нулю ,
поскольку до замыкания ток был равен нулю и, исходя из свойств катушки индуктивности, не мог измениться
скачком.
ЭДС равна сумме напряжений на резисторе и на катушке индуктивности:
Напряжение на резисторе определяется формулой:
Напряжение в катушке индуктивности определяется выражением:
Тогда ЭДС равна:
Поскольку , то в начальный момент времени напряжение на резисторе также равно нулю, а напряжение на
катушке индуктивности максимально и равно ЭДС:
(при
).
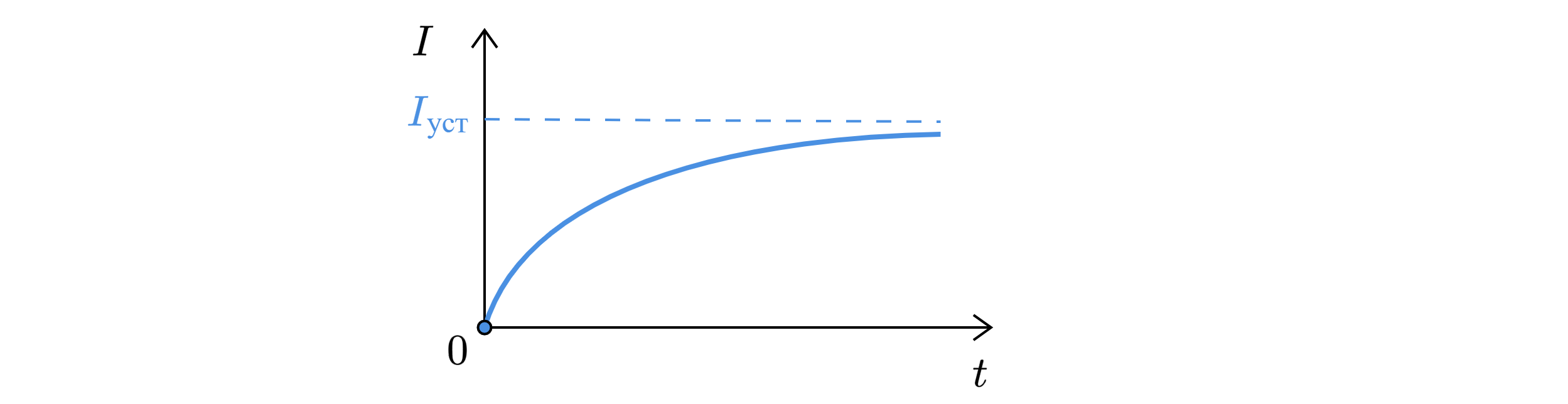
Шаг 3: ключ замкнули давно. С течением времени сила тока увеличивается, а скорость изменения
силы тока уменьшается.

Сила тока плавно увеличивается до установившегося значения . Поскольку при установившемся режиме
идеальную катушку индуктивности можно рассматривать как провод, напряжение в ней равно нулю
. Тогда
установившееся значение силы тока в цепи равно:
Пример №2
Рассмотрим электрическую цепь, состоящую из источника с внутренним сопротивлением
и параллельно
подключенных резистора
и катушки индуктивности
.
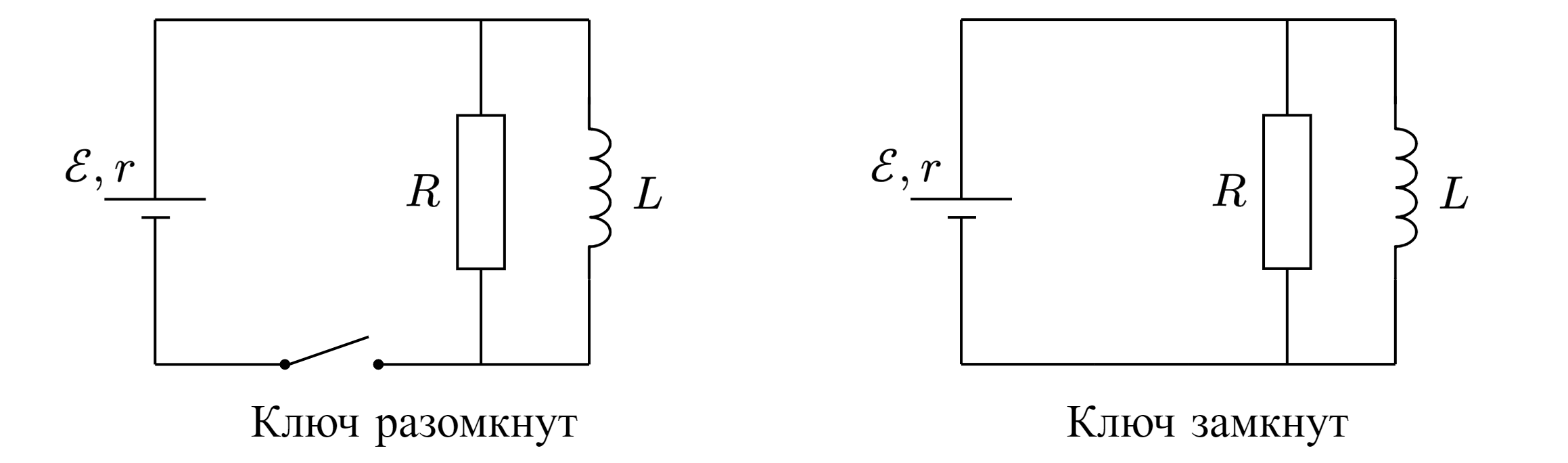
Шаг 1: ключ разомкнут. В начальный момент времени (до замыкания ключа) сила тока на катушке индуктивности и в целом в цепи равна нулю.
Шаг 2: ключ только что замкнули. Сразу после замыкания ключа сила тока в катушке равна нулю
, поскольку, исходя из свойств катушки индукутивности, сила тока в ней не меняется скачком. В резисторе
же сила тока может резко меняться и поэтому ток в цепи сразу после замыкания ключа будет протекать по синему
контуру (см. рисунок ниже).
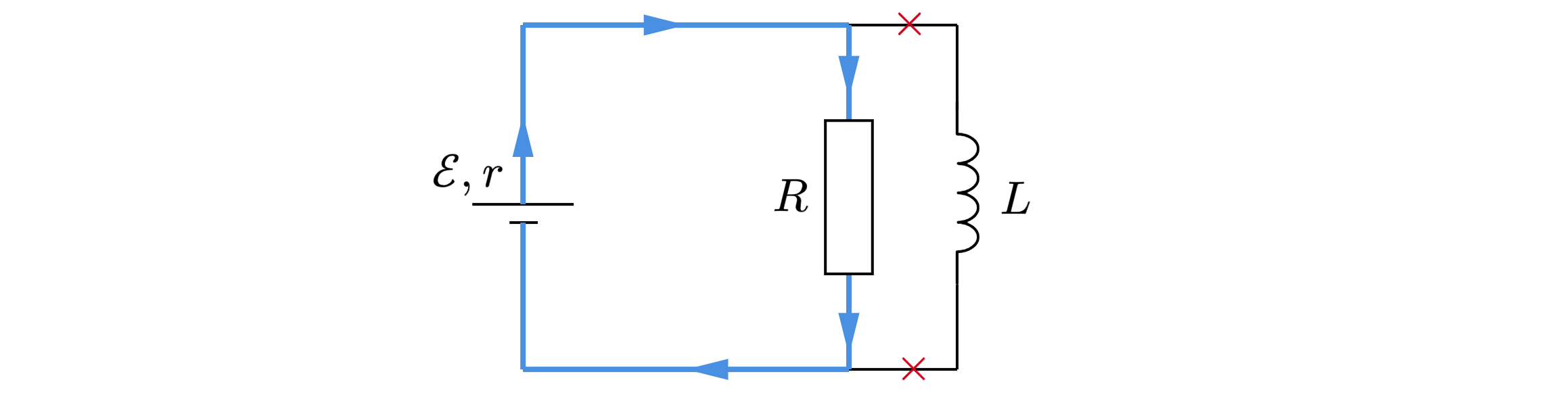
Таким образом, ток через источник в начальный момент времени определяется законом Ома для данной цепи:
Напряжение на катушке равно напряжению на резисторе, поскольку данные элементы соединены параллельно:
Шаг 3: ключ замкнут давно. Исходя из свойств катушки индуктивности, при установившемся режиме (= через длительный промежуток времени) сила тока в катушке постоянна и напряжение равно нулю:
При установившемся режиме напряжение на резисторе также равно напряжению на катушке, поскольку данные элементы соединены параллельно:
То есть при установившемся режиме ток через резистор не идет, а протекает по зеленому контуру (см. рисунок ниже).
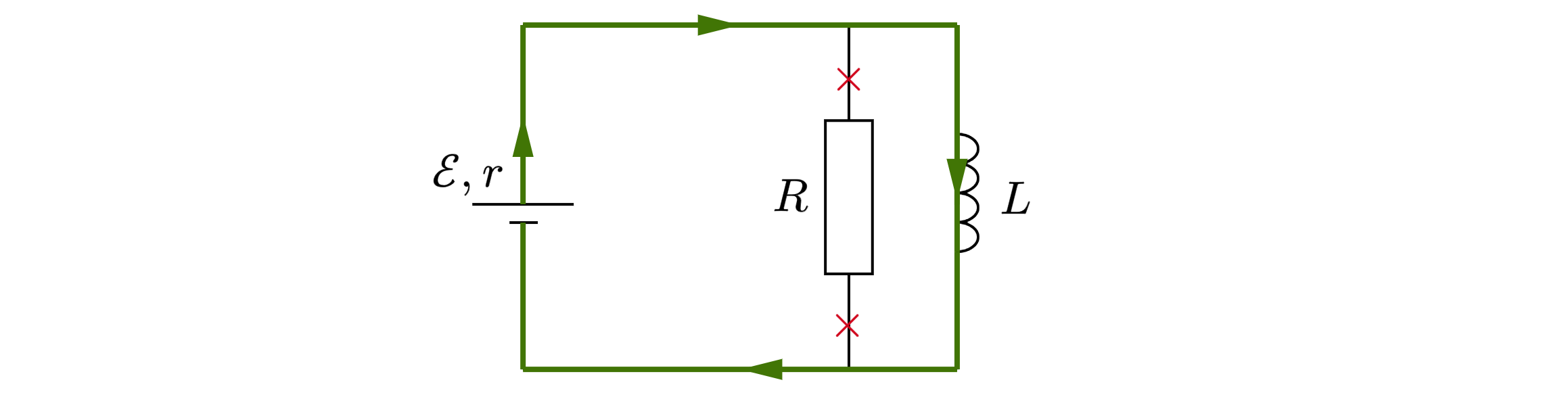
Сила тока в цепи при установившемся режиме равна:
Вывод формулы энергии, запасенной в катушке индуктивности
ЭДС самоиндукции есть работа сторонних сил по перемещению заряда:
Работа сторонних сил в свою очередь:
Полная работа сторонних сил:
Посчитаем сумму графически — построим график вида :
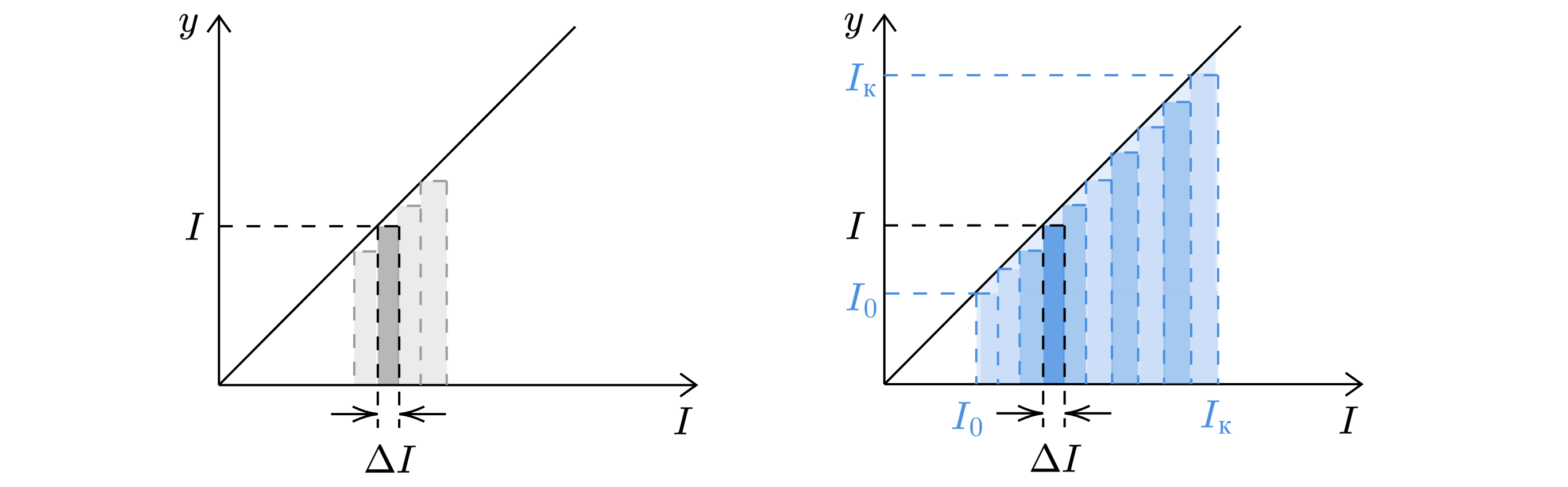
Компоненты и
назовем начальной и конечной энергией, запасенной в катушке индуктивности,
соответственно:
Тот же результат можно получить при помощи интегрирования:
