Математика в физике

Производная

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Математика в физике

Теоретическая справка

#890

Аналитический смысл производной

Определения и свойства

Производная функции $f(x)$ — это тоже некоторая функция, обозначаемая как $f′(x),$ которая определенным образом характеризует функцию $f(x).$ Как именно производная характеризует функцию и как ее находить, мы разберем дальше.

Если взять любое $x0$ из области определения функции $f(x)$ и подставить в производную $′ f(x),$ то мы получим некоторое конкретное число $f′(x0),$ равное значению производной в точке $x0.$

Следует также сказать, что не у любой функции есть производная и не в любой точке $x0$ производная существует. Далее мы будем рассматривать только такие функции, которые имеют производную во всех точках области определения.

Что мы можем понять о функции $f(x),$ зная ее производную или зная, как выглядит график ее производной?

1) Если производная $f′(x)$ функции $f (x)$ положительна на промежутке $(a;b),$ то функция $f(x)$ на этом промежутке возрастает.

2) Если производная $f′(x)$ функции $f (x)$ отрицательна на промежутке $(a;b),$ то функция $f (x)$ на этом промежутке убывает.

Для остальных свойств нам понадобится ввести еще несколько определений.

Определение: Точка $x0$ называется точкой экстремума функции $f(x),$ если в некоторой её окрестности, которая не включает в себя саму точку $x0,$ выполняется либо неравенство $f(x0) >f (x)$ (тогда точка называется точкой максимума), либо $f(x0)< f(x)$ (тогда точка называется точкой минимума).

Рассмотрим условия, при которых точка является точкой экстремума. Если в точке $x0$ функция меняется с возрастающей на убывающую или наоборот, то точка $x0$ является точкой экстремума. Причем точки, в которых при проходе слева направо функция меняет свой характер монотонности с возрастания на убывание, являются точками максимума $(xmax),$ а точки, в которых — с убывания на возрастание, являются точками минимума $(xmin).$

Вот как на графике функции $f(x)$ выглядят точки экстремума:

$PIC$

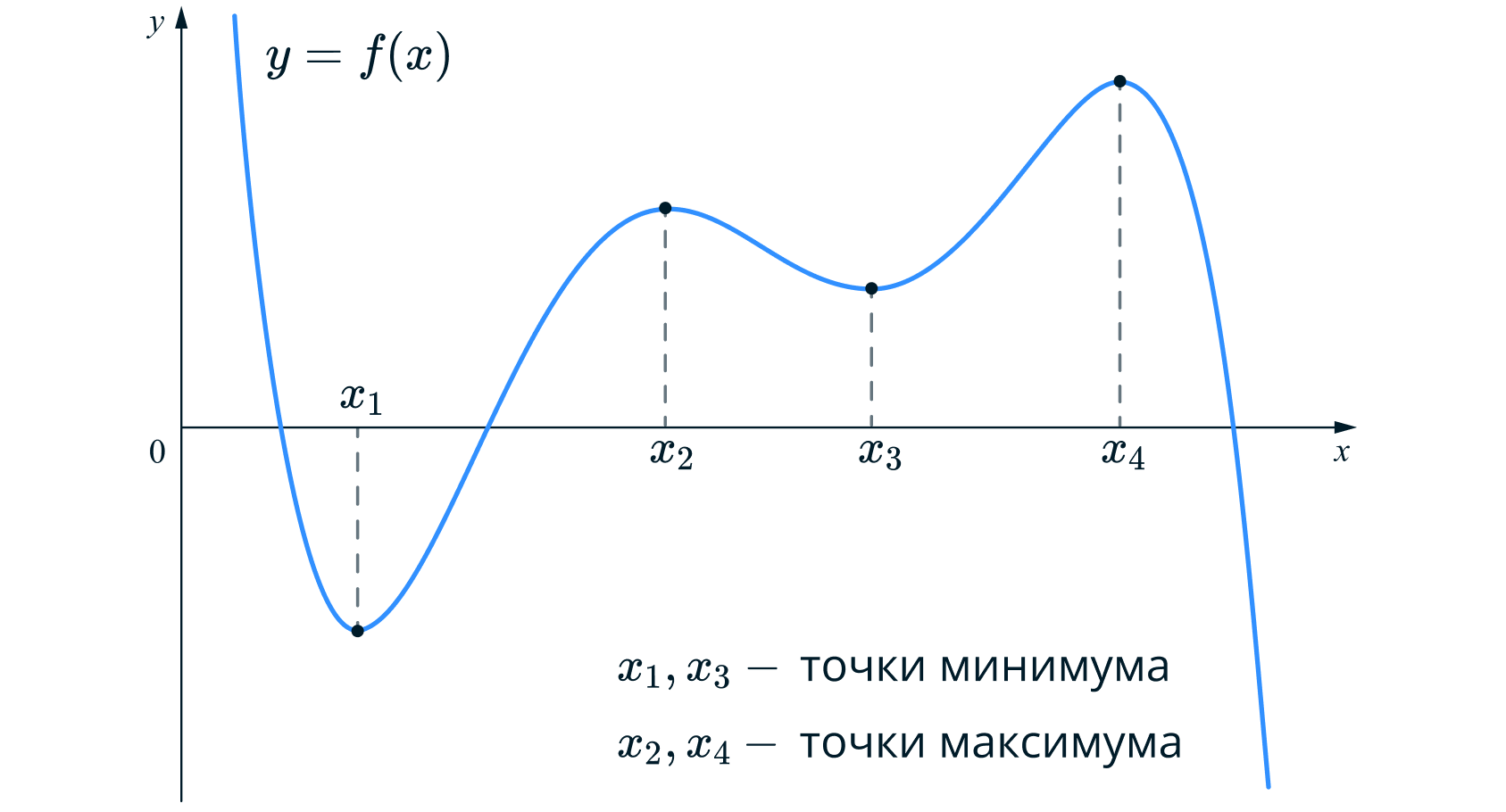
Теперь давайте подумаем. Если в точке максимума функция меняется с возрастающей на убывающую, то, учитывая свойства 1) и 2), производная, проходя через эту точку, меняется с положительной на отрицательную. Значит, в точке максимума $xmax$ производная равна нулю.
Аналогично в точке минимума $xmin$ производная равна нулю, но меняет свои значения уже с отрицательных на положительные (если смотреть слева направо).
Вот как на графике производной $f′(x)$ выглядят точки экстремума функции $f(x)$ :

$PIC$

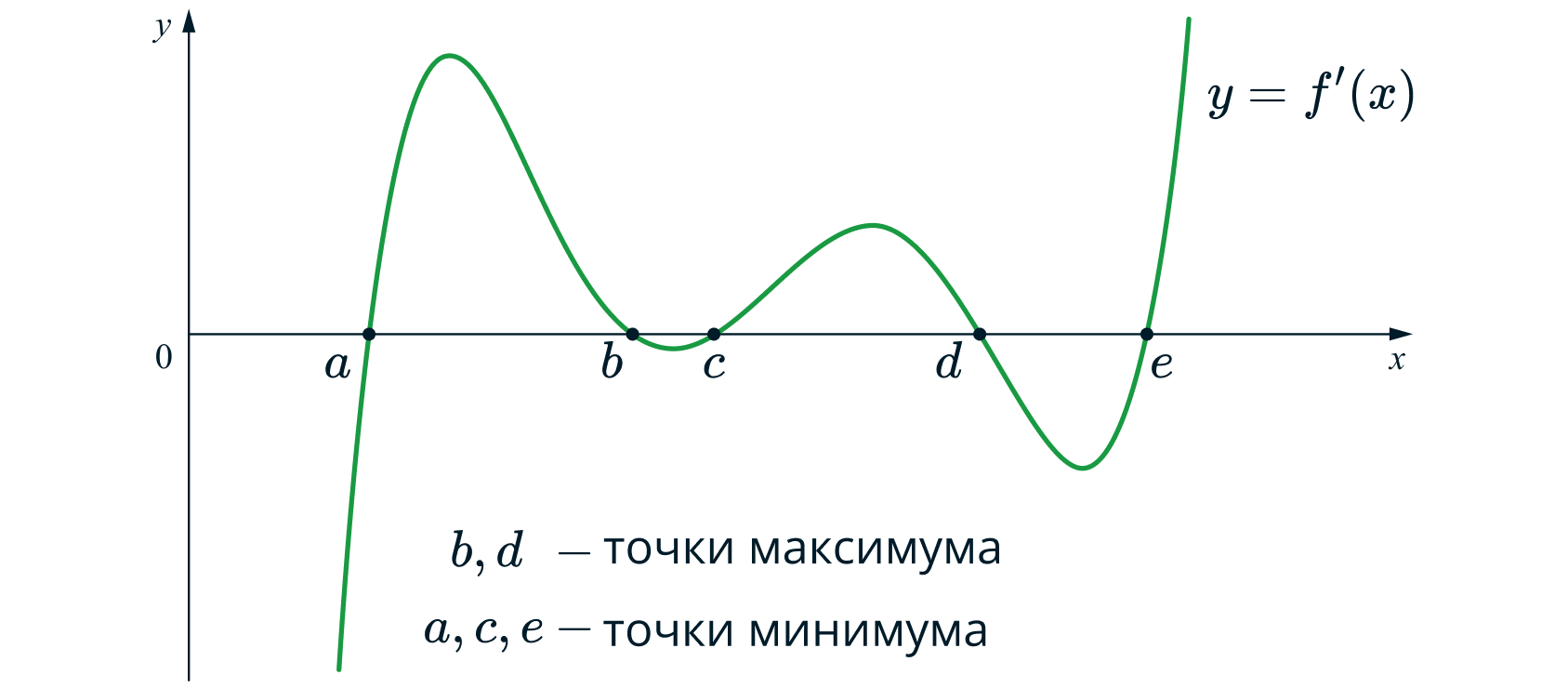
Таким образом, получаем еще два свойства:
3) Если производная $f′(x)$ в точке $x0$ равна нулю и меняет свой знак с « $+$ » на « $−$ » (то есть график пересекает ось абсцисс «сверху вниз»), если смотреть слева направо, то точка $x0$ — точка максимума функции $f(x).$

4) Если производная $f′(x)$ в точке $x 0$ равна нулю и меняет свой знак с « $−$ » на « $+$ » (то есть график пересекает ось абсцисс «снизу вверх»), если смотреть слева направо, то точка $x0$ — точка минимума функции $f(x).$
Обобщая все вышесказанное, отметим важные пункты, на которые стоит обратить внимание.

Если при решении задач вам дан график, обязательно обратите внимание на то, график чего вам дан: функции $f(x)$ или ее производной $f′(x)!$
При работе с производной мы обращаем внимание только на то, где производная $f′(x)$ положительна, отрицательна и равна нулю.
При работе с самой функцией мы обращаем внимание на то, где функция $f(x)$ возрастает, убывает и где она имеет экстремум.
Во фразе «производная функции $f(x)$ » речь идет о производной.

Краткий справочник

$PIC$

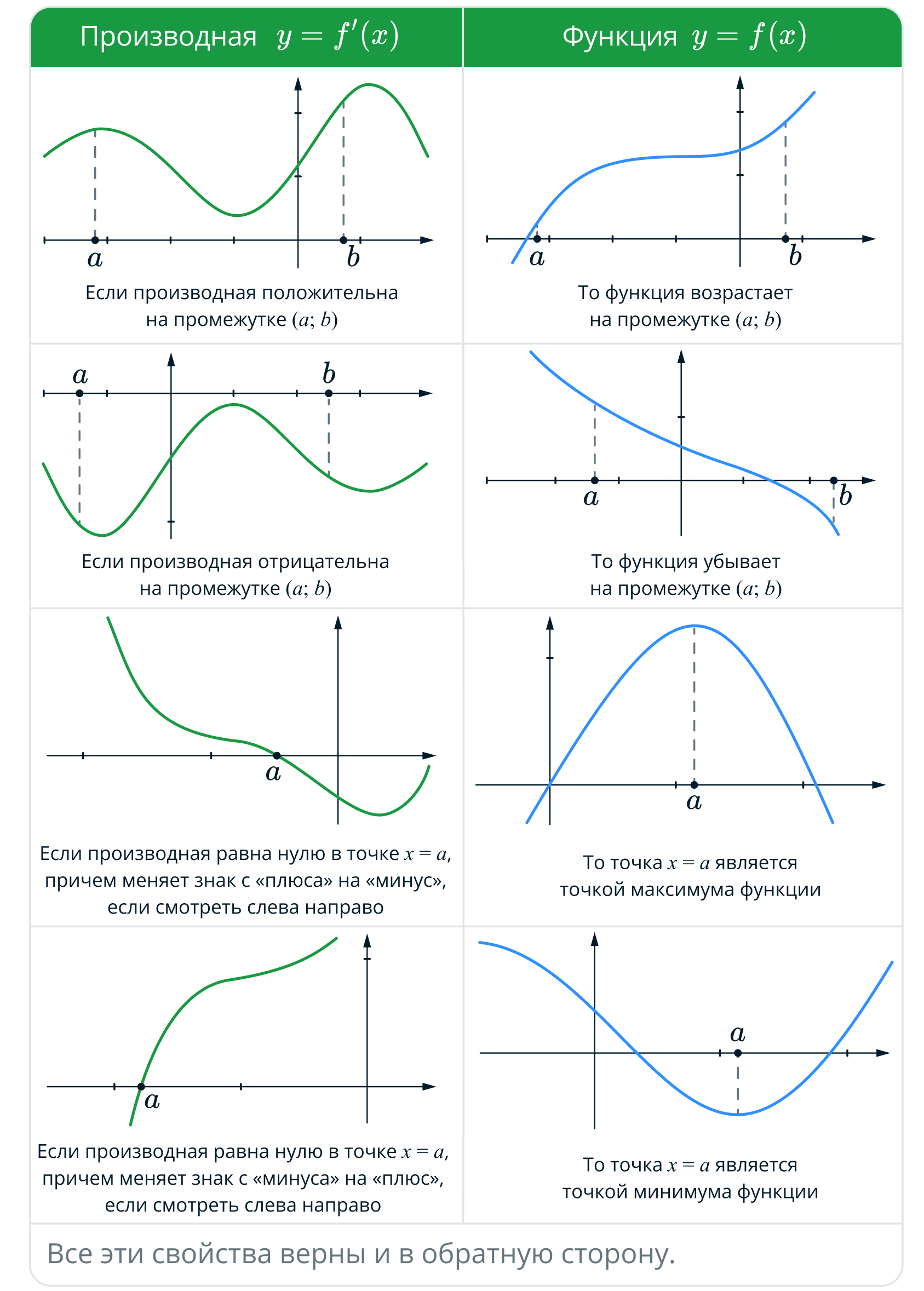
Геометрический смысл производной

Определения и свойства

Перейдем к геометрическому смыслу производной. Для начала вспомним некоторые факты об уравнениях прямых.

Линейная функция — функция вида $f(x)= kx+ b,$ где $k,$ $b$ — некоторые числа.
Графиком линейной функции является прямая.
Если $b= 0,$ то прямая проходит через начало координат.
Графиком $x= a$ является прямая, параллельная оси $Oy.$
Графиком $y = b$ является прямая, параллельная оси $Ox.$
Если две прямые $y =k1x +b1$ и $y =k2x +b2$ параллельны, то $k1 = k2.$
Для $f(x) =kx + b$ угловой коэффициент $k$ равен тангенсу угла наклона прямой к положительному направлению оси $Ox$ (сокращенно будем говорить «угол наклона»).

$PIC$

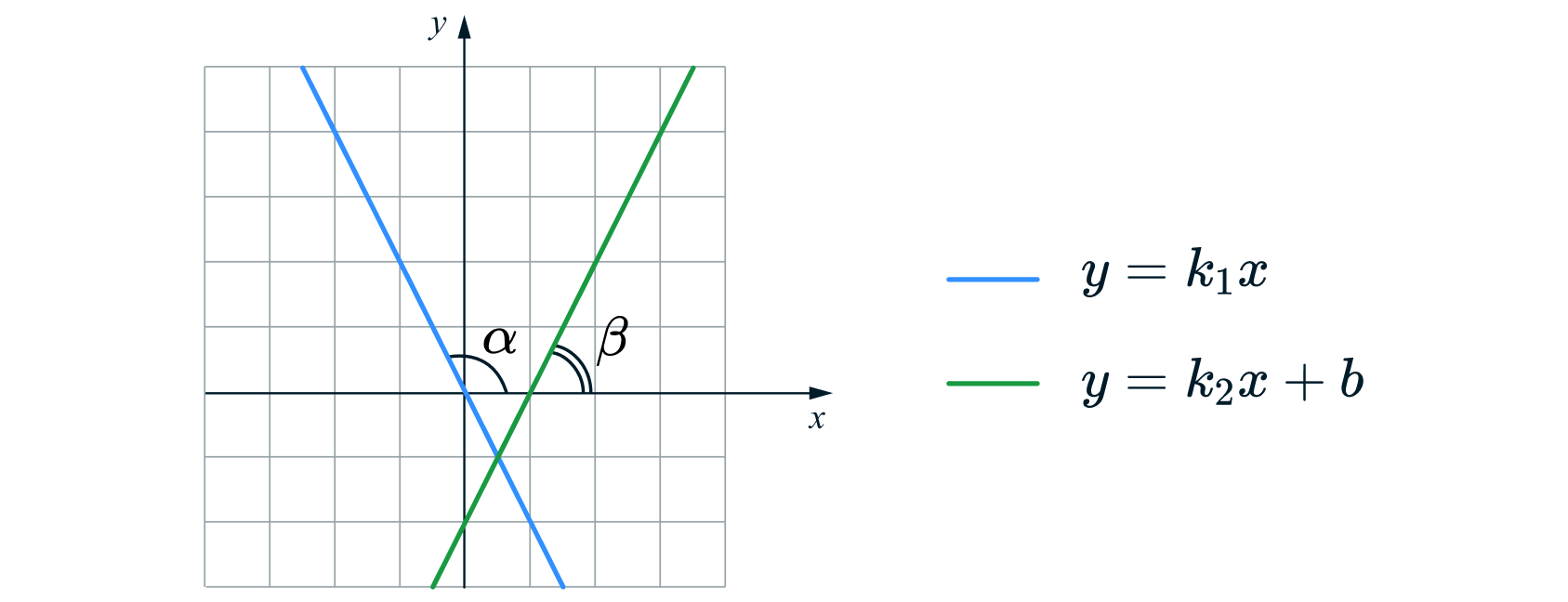
Таким образом, на картинке выше $k1 = tg α,$ $k2 = tgβ.$

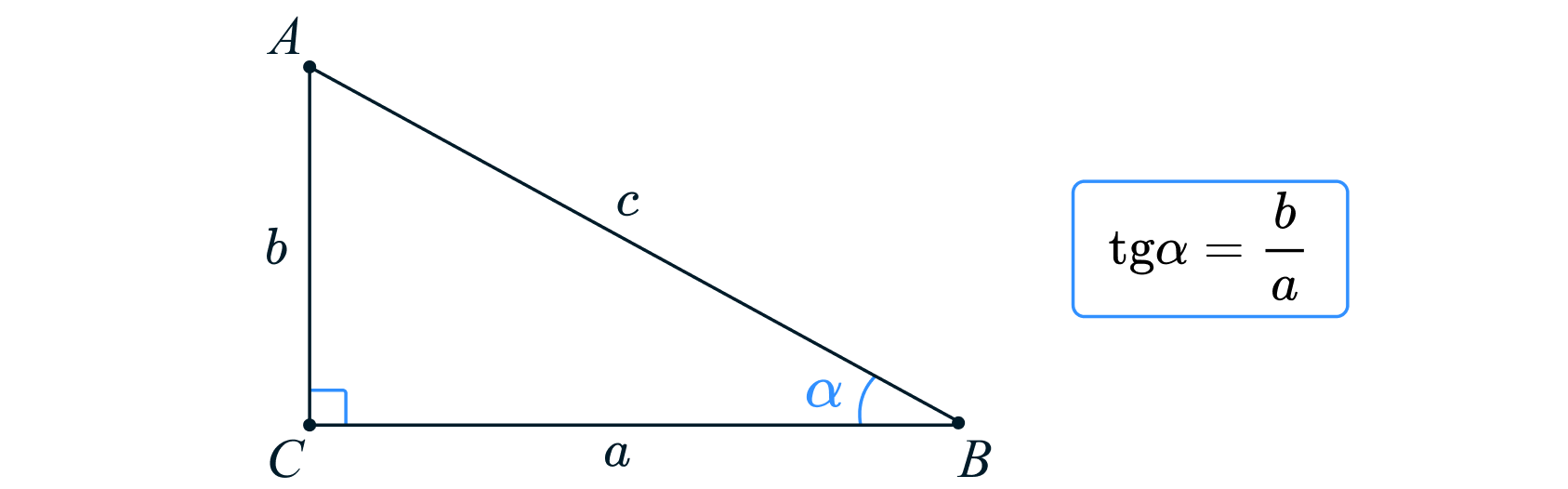
Напомним, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:

$PIC$

Итак, каков геометрический смысл производной? Если функция в точке $x0$ имеет производную, то это значит, что в этой точке можно провести касательную к графику данной функции. Касательная — это некоторая прямая, которая касается графика функции в точке $x0,$ это выглядит так:

$PIC$

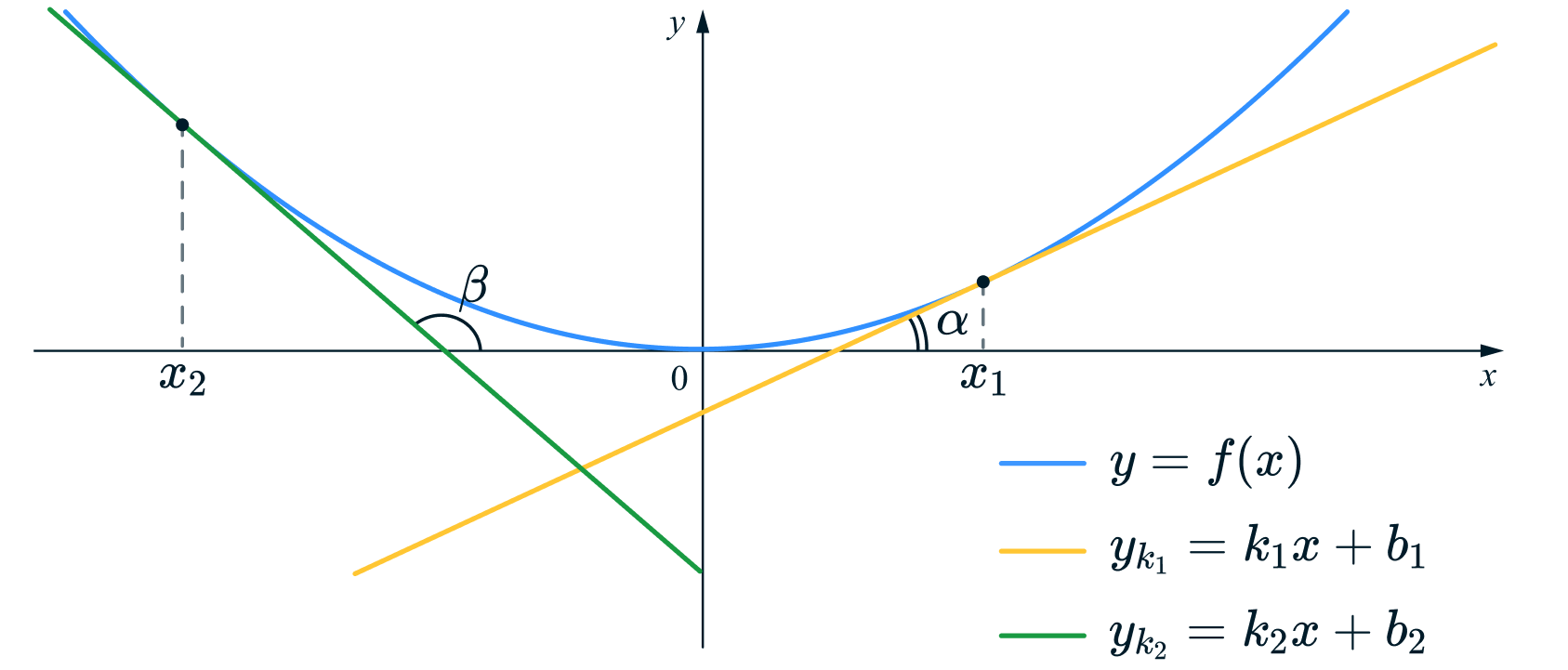
На чертеже изображены две различные касательные $yk1$ и $yk2,$ проведенные к графику функции $f(x)$ в точках $x1$ и $x2.$
Угол наклона касательной $yk1$ равен $α,$ угол наклона касательной $yk2$ равен $β.$
Если нам известно уравнение $y = f(x)$ функции, то, выбрав точку $x0,$ в которой мы хотим провести касательную к графику этой функции, можно записать уравнение этой касательной:

yk = f(x0)+ f′(x0)⋅(x− x0)

Если переписать уравнение касательной так, чтобы первое слагаемое было $kx,$ то есть записать в виде $yk = f′(x0)⋅x +f (x0)− f′(x0)⋅x0,$ то получим

( { k = f′(x0) ( b= f(x0)− f ′(x0)⋅x0

Таким образом, с одной стороны, угловой коэффициент $k$ касательной, как и любой прямой, равен тангенсу угла наклона $α.$ С другой стороны, если эта прямая касается графика функции $f(x)$ в точке $x0,$ то угловой коэффициент $k$ также равен числу $f′(x0).$ Тогда получаем

tgα = k = f′(x ) 0

Таким образом, геометрический смысл производной заключается в следующем: если к графику функции $f(x)$ в некоторой точке $x 0$ проведена касательная, то значение производной в точке касания равно тангенс угла наклона касательной, то есть $′ f (x0 ) = tgα.$

Физический смысл производной

Если положение точки при ее движении по прямой задается функцией $x= x(t),$ где $t$ — время движения, a $x$ — расстояние от движущейся точки до точки $x= 0,$ то производная функции $x$ — это функция скорости, то есть

x′(t)= v(t).

Вторая производная функции $x$ (или первая производная функции $v$ ) — это функция ускорения, то есть

x′′(t) =v′(t)= a(t).

Предыдущая справка

Следующая справка