Функция квадратного корня
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#889
Функция квадратного корня
Исследуем свойства функции а затем построим график этой функции.
-
Из определения квадратного корня следует, что область определения и множество значений этой функции — множество неотрицательных вещественных чисел.
Тогда график функции
будет расположен в первой четверти системы координат.
- Функция ограничена снизу. Она не имеет наибольшего значения, а наименьшее значение равно нулю.
- Функция не является ни четной, ни нечетной.
- Функция непериодическая.
- График функции пересекает оси
и
в точке
-
является нулем функции.
Функция принимает положительные значения на промежутке
Отрицательные значения функция не принимает.
- Если
то
то есть функция возрастает на всей области определения.
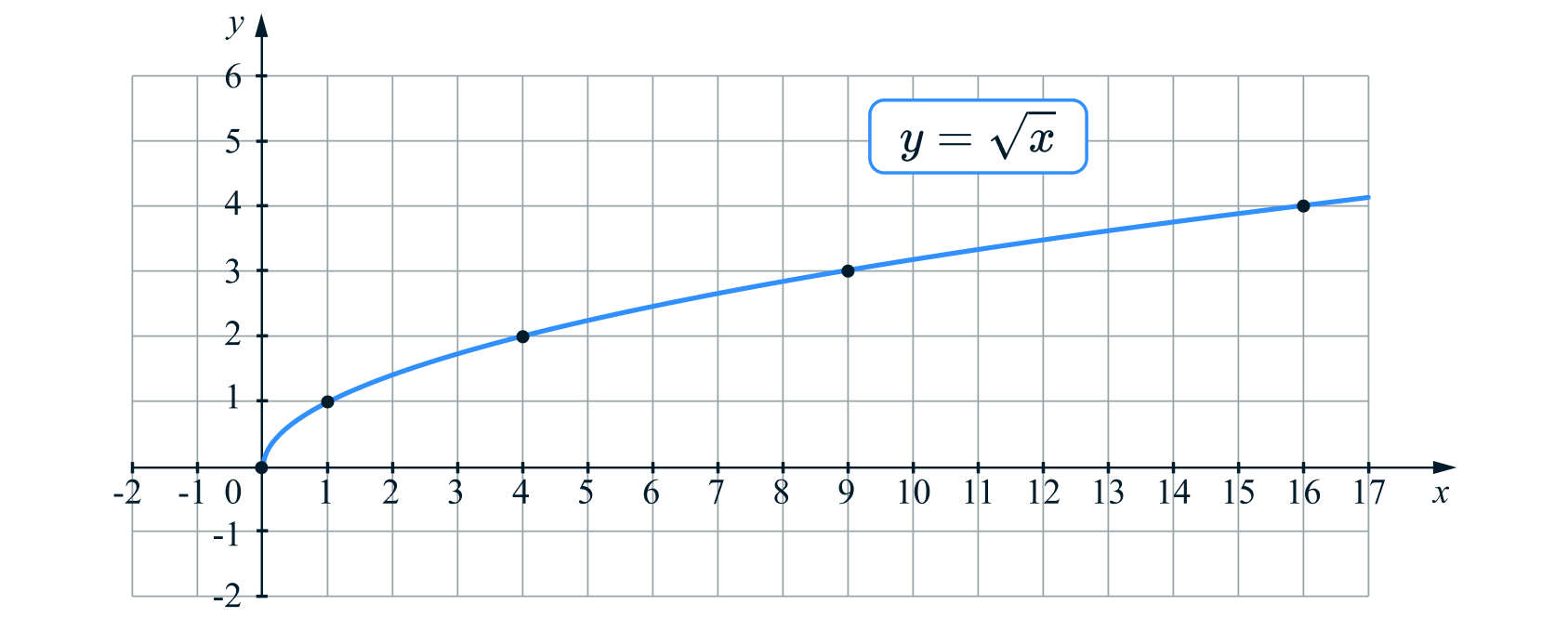
Теперь построим график функции Составим таблицу значений:
| | | | 4 | 9 | 16 |
| | 0 | 1 | 2 | 3 | 4 |
Отметим полученные точки в системе координат и соединим их плавной линией, учитывая вышеперечисленные свойства: