Кинематика. Равноускоренное прямолинейное движение
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#957
Основные формулы
Равномерное прямолинейное движение
Перемещение:
|
|
Зависимость координаты от времени:
|
|
Равноускоренное прямолинейное движение
Ускорение тела:
|
|
Зависимость скорости от времени:
|
|
Зависимость координаты от времени:
|
|
Перемещение:
|
|
Перемещение, «формула без времени»:
|
|
Перемещение, «формула без ускорения»:
|
|
Механическое движение
Механическое движение тела — изменение положения тела в пространстве относительно других тел с течением времени. При механическом движении тела взаимодействуют по законам механики.
Кинематика описывает геометрические свойства движения без учета причин, которые его вызывают. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел во времени.
Материальная точка — это тело, размеры которого очень малы по сравнению с расстоянием, которое оно прошло, поэтому этими размерами можно пренебречь. В кинематике все тела принято рассматривать как материальные точки.
Основные понятия
- Траектория — линия, вдоль которой движется тело.
- Путь — длина участка траектории, пройденного телом за определенный промежуток времени.
- Радиус-вектор — вектор, проведенный из начала координат в место расположения материальной точки. Положение материальной точки в пространстве задается радиус-вектором.
- Перемещение — вектор, соединяющий начальное и конечное положение тела.
- Система отсчета — тело отсчета (начало координат) вместе с жестко связанной с ним системой координат и часами.
Для лучшего понимания разницы между понятиями пути и перемещения снизу изображен поясняющий рисунок.

Кинематические характеристики движения материальной точки
Перемещение — вектор, соединяющий два последовательных положения материальной точки на траектории. Перемещение является вектором-разностью радиус-векторов конечного и начального положений тела.
Графический метод нахождения перемещения и пройденного пути: для определения проекции
перемещения нужно найти численно равную ей площадь под графиком проекции скорости
.
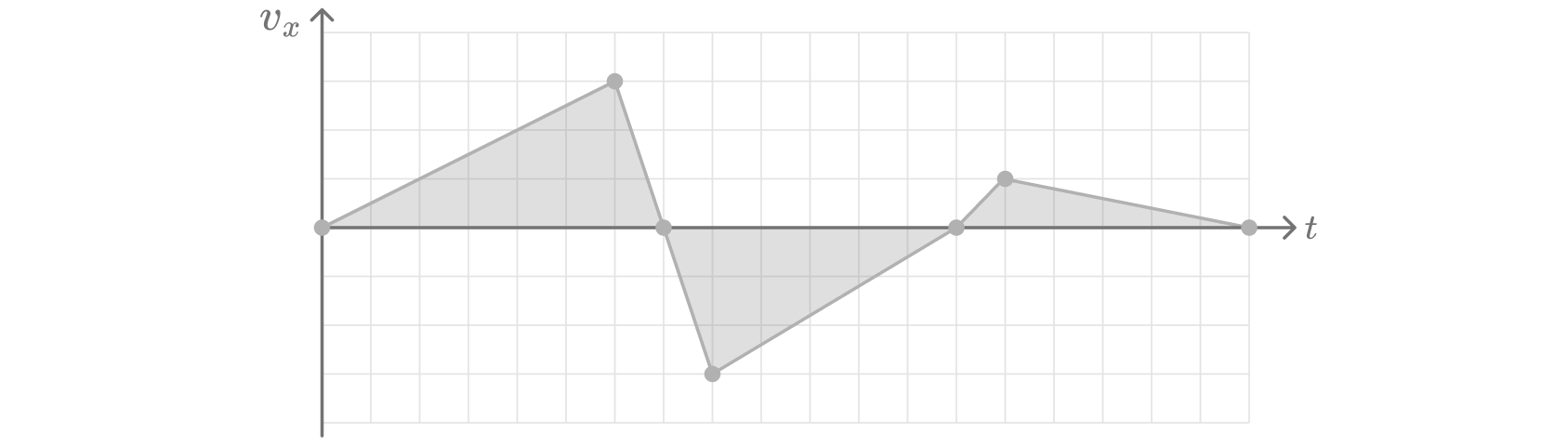
Скорость — векторная физическая величина, которая характеризует быстроту изменения положения материальной точки в пространстве с течением времени.
|
|
Единицы измерения:
м/с (метр в секунду).
Вектор скорости — это первая производная от радиус-вектора по времени.
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости по величине и по направлению.
|
|
где и
— конечная и начальная скорость соответственно.
В проекции на ось :
|
|
где и
— проекция конечной и начальной скорости на ось
соответственно.
Единицы измерения:
(метр в секунду за секунду).
Вектор ускорения — это первая производная от скорости по времени и вторая производная от радиус-вектора по времени.
Вектор ускорения сонаправлен с вектором скорости при равноускоренном движении и противоположно направлен при равнозамедленном движении.
Прямолинейное равномерное движение
Прямолинейное равномерное движение (ПРД) — движение, при котором тело за равные промежутки времени совершает одинаковые перемещения.
Траектория ПРД — прямая. При этом скорость остается постоянной .

Уравнение движения материальной точки:
|
|
Скорость движения материальной точки:
|
|
Ускорение материальной точки:
|
|
Пройденный путь:
|
|
Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение (ПРУД) материальной точки — движение с постоянным
вектором ускорения . Траекторией ПРУД является парабола.
Уравнение движения материальной точки:
|
|
Скорость движения материальной точки:
|
|
Ускорение материальной точки:
|
|
Перемещение:
|
|
Перемещение, «формула без времени»:
|
|
Перемещение, «формула без ускорения»:
|
|
Выведем все формулы для перемещения при ПРУД. Для этого вспомним определение ускорения:
|
|
Данная зависимость является линейной, потому что переменная имеет первую степень. То есть
график будет иметь вид прямой. Сравним с общим видом уравнения прямой
.
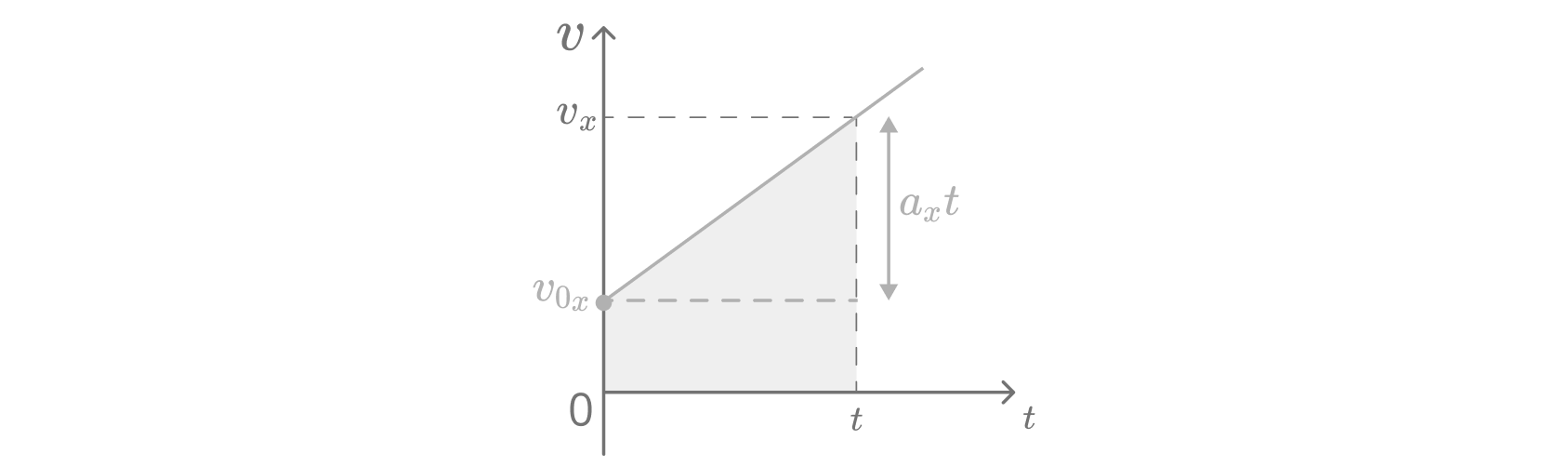
Отрезок от до
равен разности этих скоростей:
. Мы уже знаем, что перемещение
при ПРУД можно найти как площадь фигуры под графиком. Разобьем синюю фигуру на две части —
прямоугольник со сторонами
и
и треугольник с основанием
и высотой
. Теперь найдем
площадь каждой фигуры и найдем сумму площадей.
|
|
Получим формулу для перемещения при ПРУД материальной точки:
|
|
Теперь посмотрим на синюю фигуру под графиком как на трапецию и найдем ее площадь (полусумма оснований на высоту). Тогда получим «формулу без ускорения»:
|
|
Обе формулы работают и в векторном представлении. Осталась еще одна формула для перемещения при ПРУД. Чтобы ее получить, запишем уравнение для перемещения при, выведенное ранее, в векторном виде:
|
|
Домножим обе части на вектор :
|
|
Представим как разность векторов конечной и начальной скоростей:
|
|
Можно заметить, что выражение можно упростить, используя формулу разности квадратов:
|
|
Произведение двух векторов называется скалярным и расписываются как
, где угол
является углом между вектором ускорения
и перемещения
. Скалярные произведения
и
расписываются как
и
соответственно. Тогда:
|
|
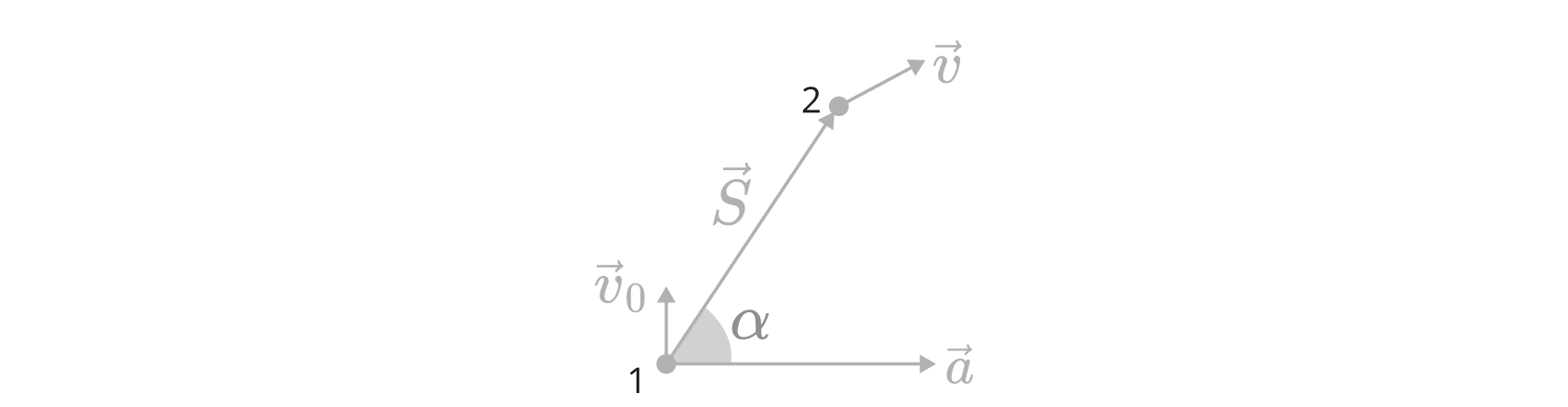
Для одной оси эта формула записывается в проекциях:
|
|
