Движение по окружности
Готовиться с нами - ЛЕГКО!
Теоретическая справка
#959
Равномерное движение по окружности
Равномерное движение по окружности — частный случай криволинейного движения, когда вектор скорости тела не изменяется по модулю (длина вектора постоянна), а изменяет лишь свое направление.
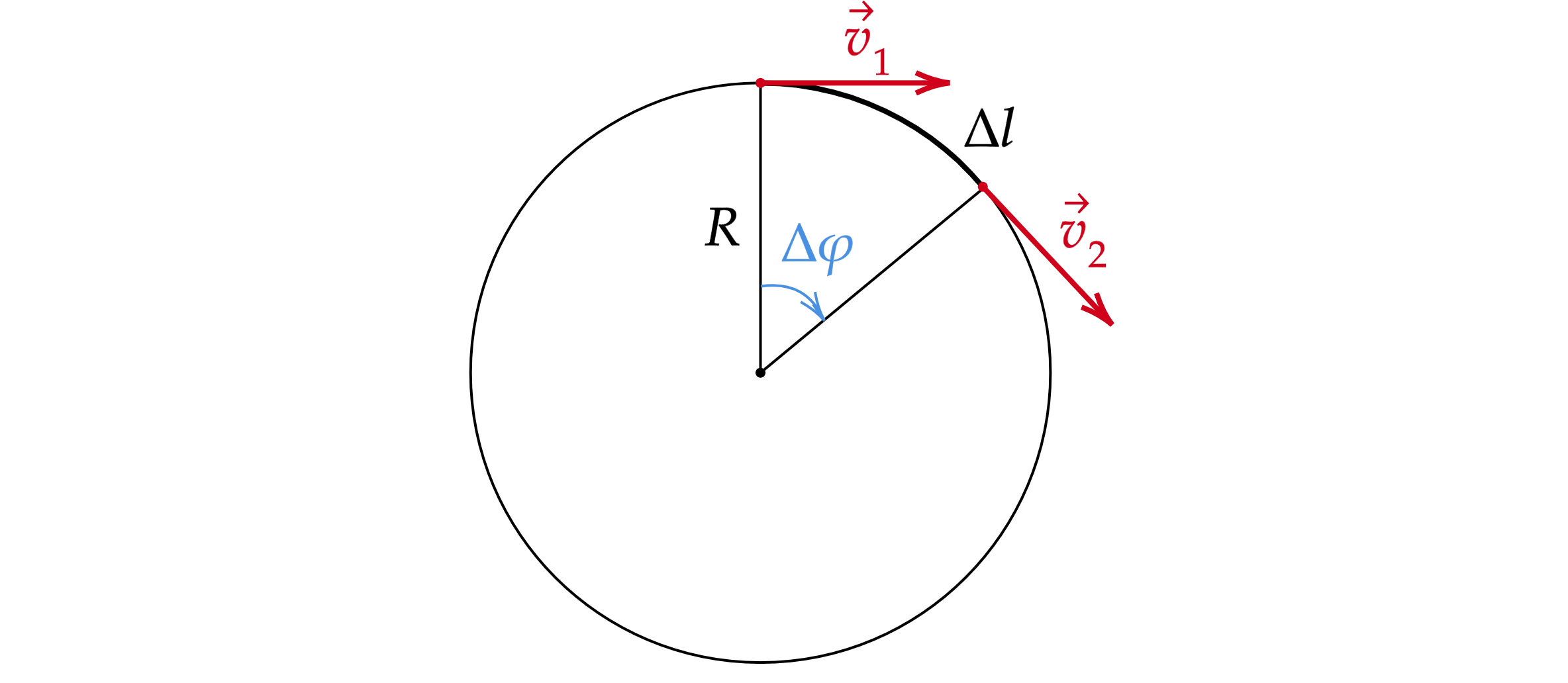
Угловая скорость в случае равномерного движения по окружности — отношение угла поворота радиуса за некоторый промежуток времени:
При неравномерном движении по окружности угловая скорость вводится как производная угла поворота по времени:
Единицы измерения: (радиан в секунду)
Связь линейной и угловой скорости
Угол поворота в радианной мере есть отношение длины дуги к радиусу:
Поскольку движение равномерное, длину дуги можно выразить через линейную скорость и время движения:
Выразим линейную скорость:
Отсюда связь линейной и угловой скорости:
Период обращения — это время одного полного оборота, то есть отношение времени обращения к числу оборотов:
Единицы измерения: (секунда).
При равномерном движении по окружности период определяется по формуле:
Частота обращения — это величина, обратная периоду. Частота показывает, сколько полных оборотов совершается в единицу времени.
Единицы измерения: (оборот в секунду)
(герц) =
Отсюда угловая скорость, выраженная через частоту и период:
Центростремительное ускорение
При равномерном движении по окружности с изменением направления вектора скорости возникает
центростремительное ускорение, направленное перпендикулярно вектору скорости в центр
окружности.
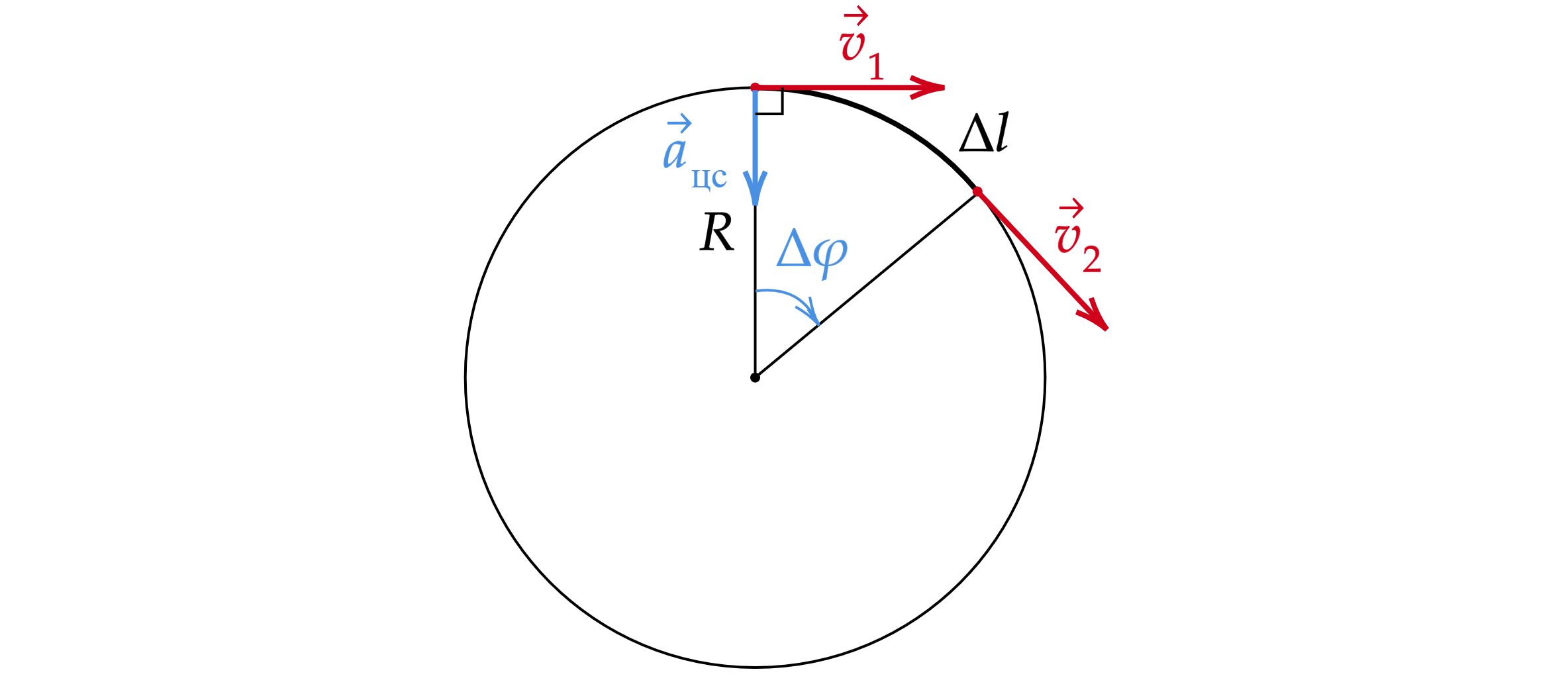
Центростремительное ускорение вычисляется по формуле:
Вывод формулы для центростремительного ускорения
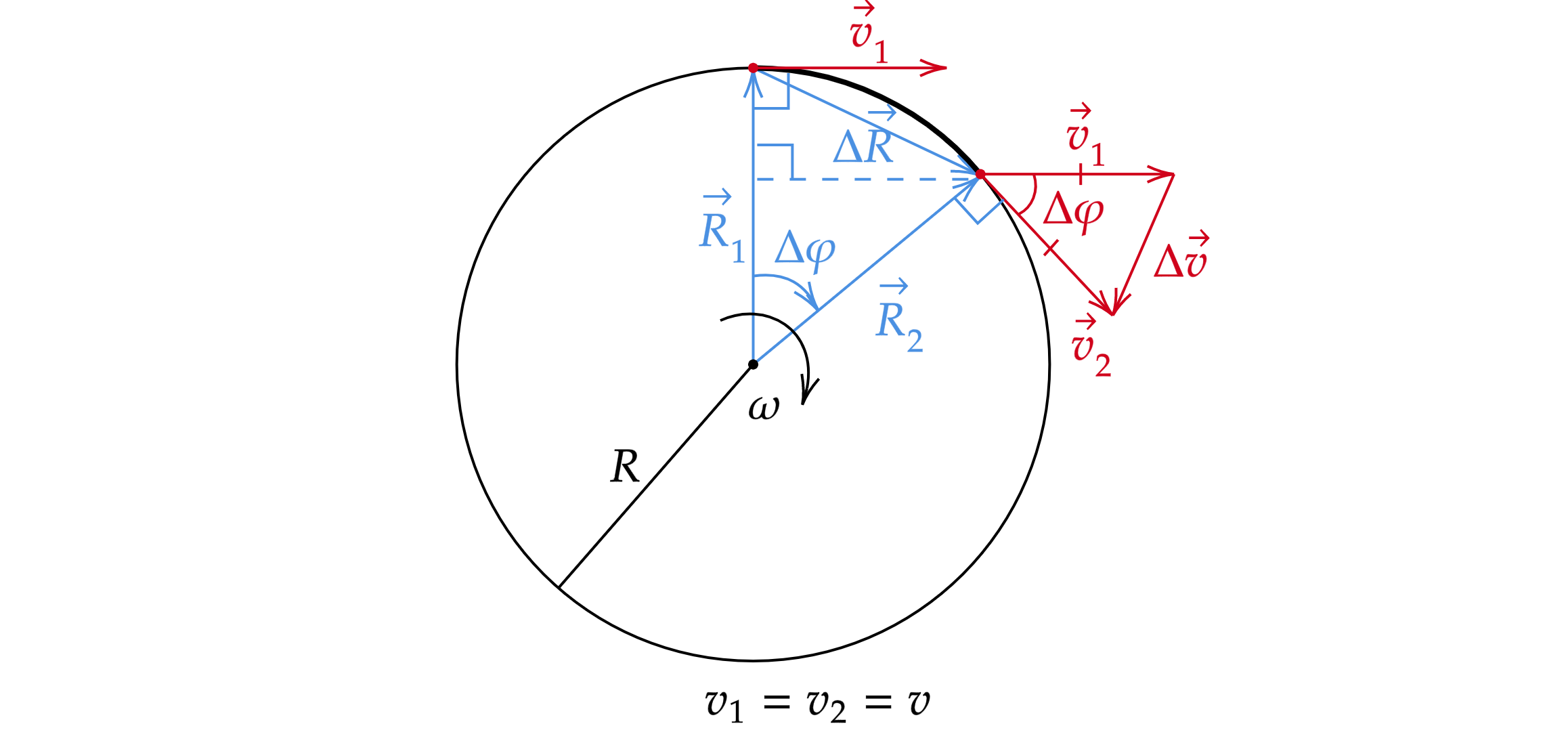
Поскольку движение по окружности равномерное, модуль линейной скорости постоянен:
Из подобия треугольников:
Преобразуем выражение и разделим обе части на :
Ускорение по определению:
Модуль ускорения равен:
С учетом этого:
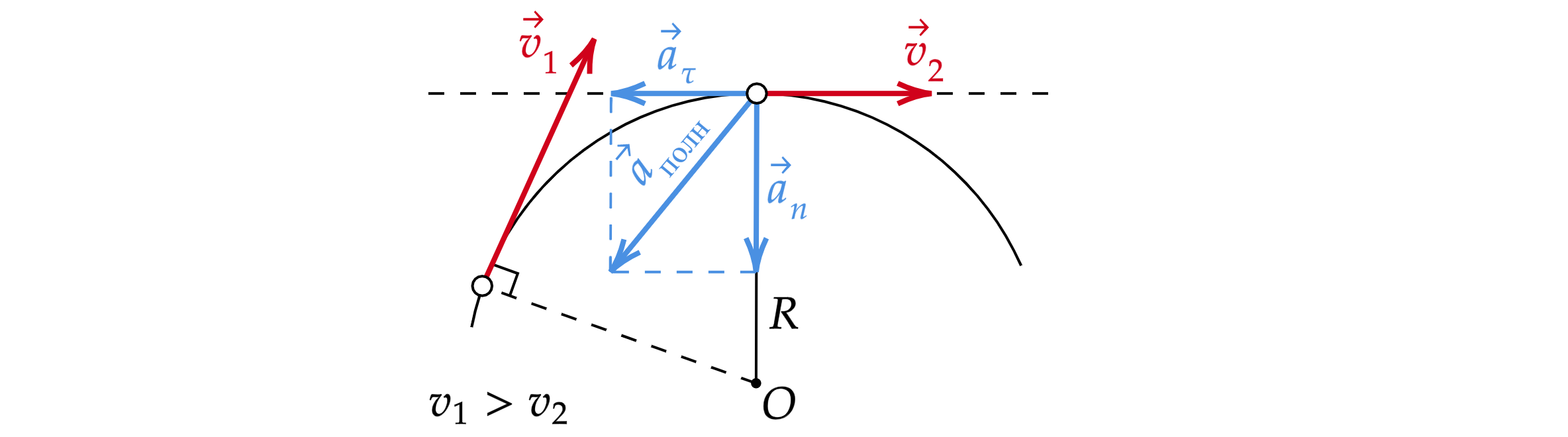
Ускорение при криволинейном движении
При криволинейном движении скорость изменяется по величине и по направлению, поэтому полное ускорение имеет две компоненты — нормальное ускорение и тангенциальное ускорение.
-
Нормальное (центростремительное) ускорение — компонента ускорения, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной, направленное перпендикулярно (по нормали) вектору скорости к центру кривизны траектории.
Единицы измерения:
(метр в секунду за секунду).
-
Тангенциальное ускорениe — компонента ускорения, направленная по касательной к траектории движения. Если модуль скорости увеличивается, то тангенциальное ускорение
направлено по касательной в направлении скорости. Если модуль скорости уменьшается, то тангенциальное ускорение
направлено по касательной в противоположном скорости направлении.
Единицы измерения:
(метр в секунду за секунду).
-
Полное ускорение тела, движущегося по окружности, равно векторной сумме тангенциального и нормального ускорений.
Или по теореме Пифагора:
Обобщим все, что касается нормального, тангенциального и полного ускорений в одной таблице.
Кинематические соотношения при движении по окружности
Соотношение 1: диск
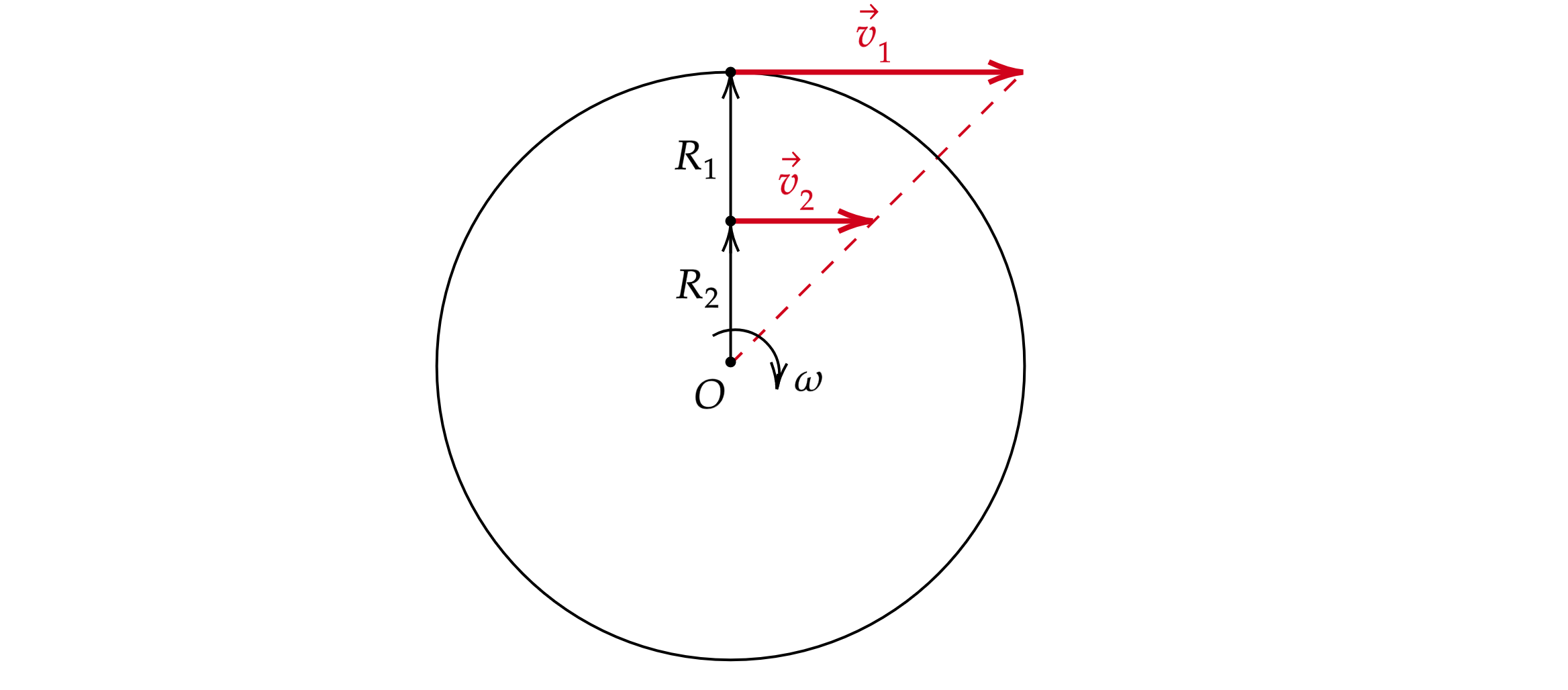
Все точки, принадлежащие одному и тому же диску, вращаются с одинаковой угловой скоростью
С учетом связи линейной и угловой скорости можно сделать вывод, что линейные скорости точек относятся прямо пропорционально их радиусам:
Чем ближе точка к центру окружности, тем меньше ее скорость, чем дальше от центра — тем скорость точки
больше. Сам же центр окружности неподвижен
.
Соотношение 2: ременная передача

Поскольку шкивы соединены ремнем и ремень не растягивается и не сжимается, линейные скорости всех точек ремня одинаковы:
Угловые скорости точек ремня могут быть разными или одинаковыми
(в зависимости от условия
задачи).
Соотношение 3: имеется точка контакта
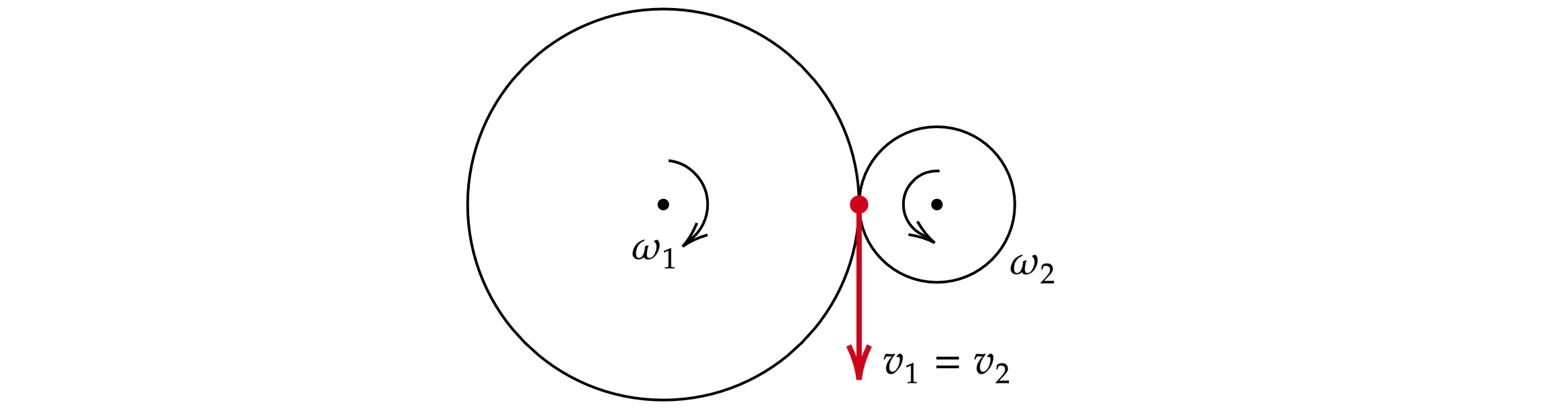
В точке контакта («зацепа») линейные скорости равны:
Угловые скорости точек «зацепа» могут быть разными или одинаковыми
(в зависимости от
условия задачи).
