Механика

Механические колебания

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Механика

Теоретическая справка

#965

Понятие о колебательном движении. Период и частота колебаний

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия.
Положением равновесия называется такое положение системы, в котором она может оставаться сколь угодно долго (будучи помещенной в это положение в состоянии покоя).
Период колебаний $T$ — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды. Единицы измерения: [ $с$ ] (секунда).
Частота колебаний $ν$ — это величина, обратная периоду:

|------| | 1-| -ν =-T-|

Частота показывает, сколько полных колебаний совершается за одну секунду. Единицы измерения: [ $Гц$ ] (герц).

Гармонические колебания. Смещение, амплитуда и фаза при гармонических колебаниях

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

|----------------| -x =-A-cos(ωt-+-φ0)

где $A$ — амплитуда колебаний тела — величина его наибольшего отклонения от положения равновесия, единицы измерения: [ $м$ ] (метр); $ω$ — циклическая частота,единицы измерения: [ $рад/с$ ] (радиан в секунду).

2π-- ω = T = 2π ν

Аргумент косинуса $(ωt + φ0)$ называется фазой колебаний. Величина $φ0$ , равная значению фазы при $t = 0$ , называется начальной фазой. Начальная фаза отвечает начальной координате тела: $x0 = A cosφ0$ .

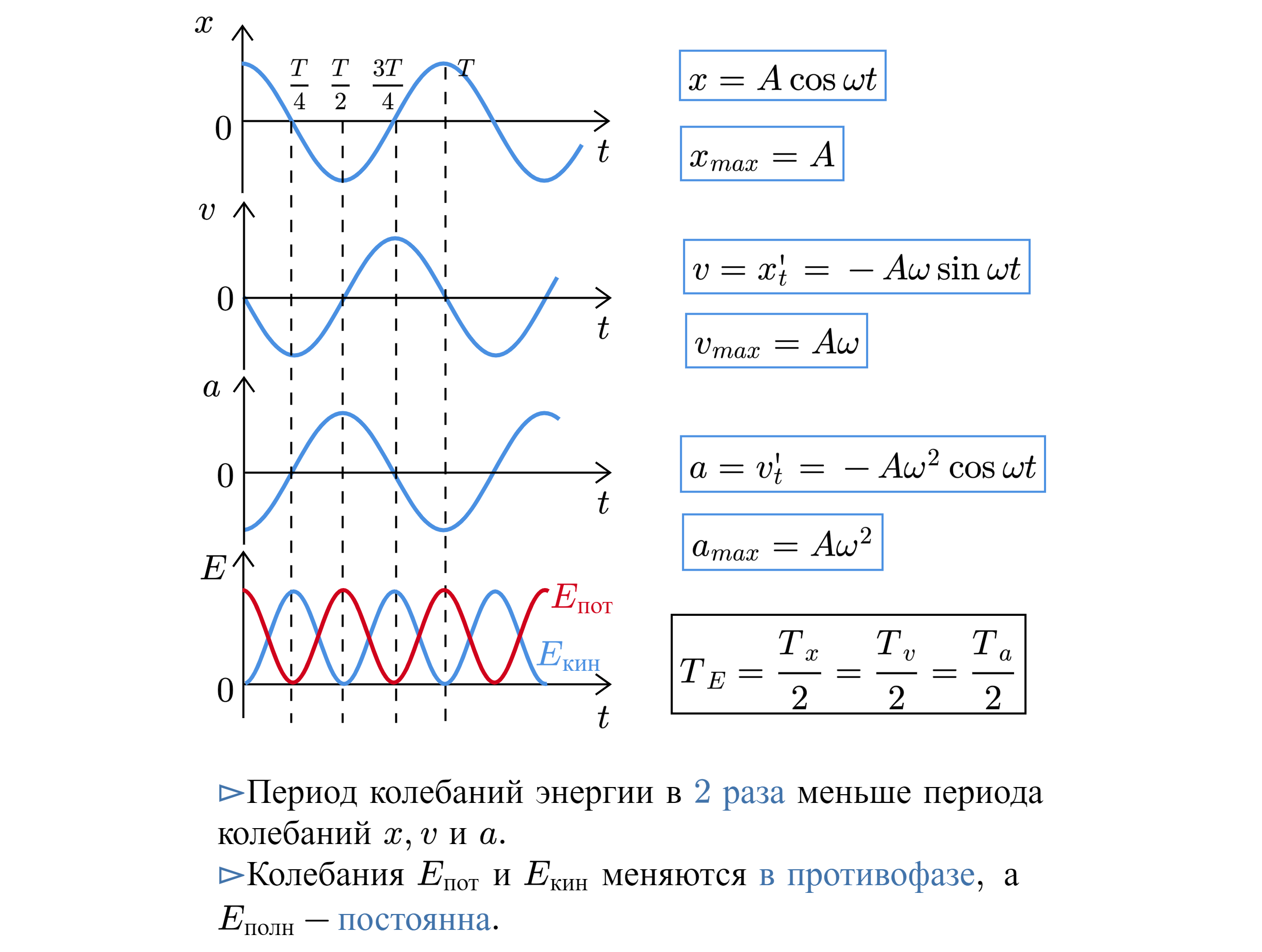
Динамика гармонических колебаний

Найдем дифференциальное уравнение, которое описывает гармонические колебания. Для этого вычислим производные функции $x = A cos(ωt +φ0 )$ по времени.

Первая производная по времени:

x′t = − Aω sin(ωt+ φ0)

Вторая производная по времени:

′′ 2 2 xtt = − A ω cos(ωt + φ0) = − ω ⋅x

Из сравнения полученных выражений следует основное уравнение динамики гармонических колебаний:

|-′′----2-----| -xtt +-ω-x =-0

Решение этого уравнения всегда будет выражение вида:

|----------------| -x =-A-cos(ωt-+-φ0)

Свободные колебания. Превращение энергии при гармонических колебаниях.

Свободные колебания — колебания системы, предоставленные самой себе (при постоянных внешних условиях).

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

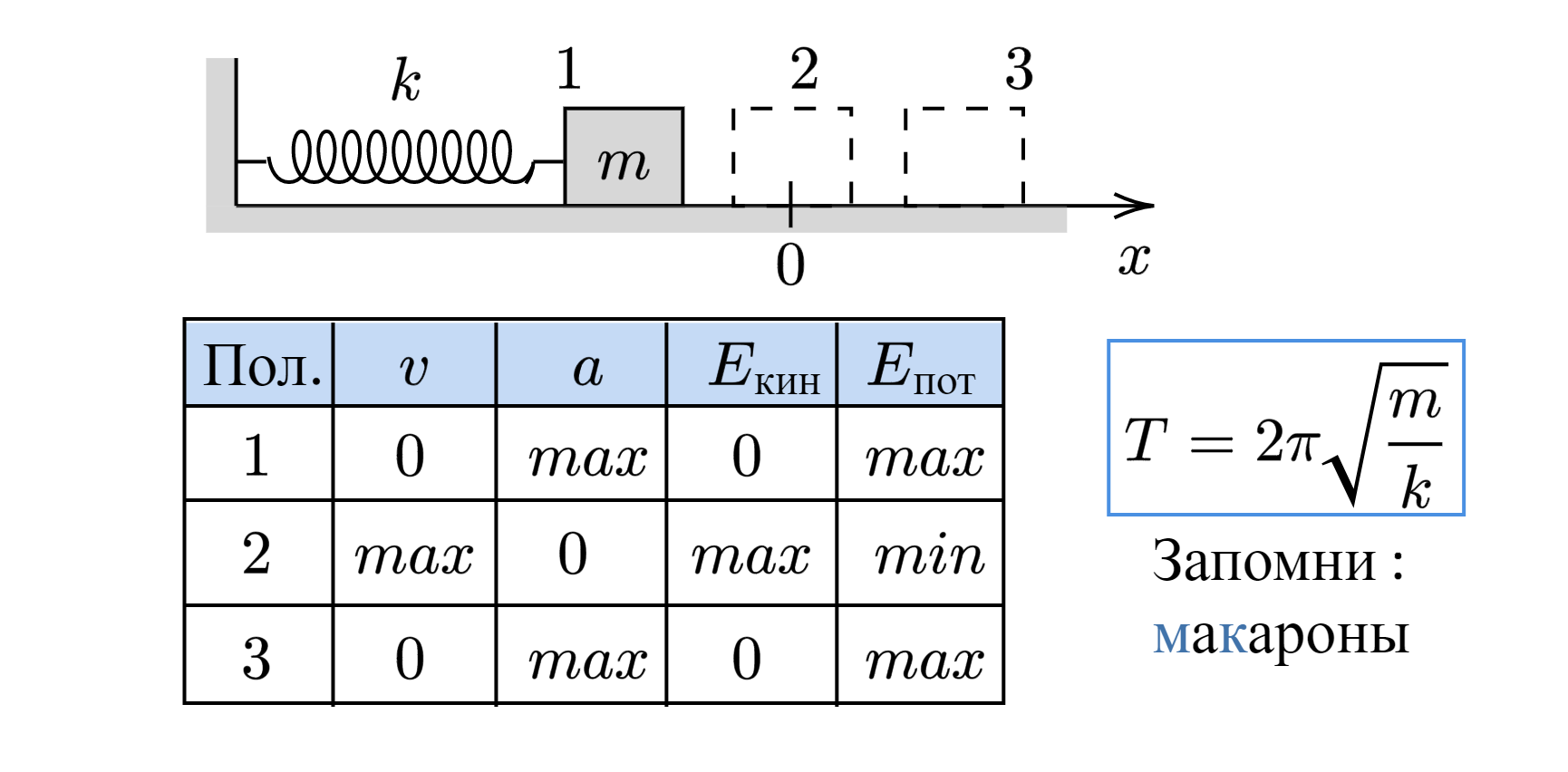
Найдём период малых горизонтальных колебаний пружинного маятника. Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу $m$ , жёсткость пружины равна $k$ . Координате $x = 0$ отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза. В горизонтальном направлении на груз действует только сила упругости $F⃗$ со стороны пружины. Второй закон Ньютона для груза в проекции на ось X имеет вид

max = Fx

Если $x > 0$ (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону и $Fx < 0$ . Наоборот, если $x < 0$ , то $Fx > 0$ . Знаки $x$ и $Fx$ всё время противоположны, поэтому закон Гука можно записать так:

F = − kx x

max = − kx

отсюда можем написать выражение для определения циклической частоты

2 k- ω = m

Отсюда и из соотношения $2π T = --- ω$ находим период горизонтальных колебаний пружинного маятника.

|------∘---| |T = 2π m-| ---------k--

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити. Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

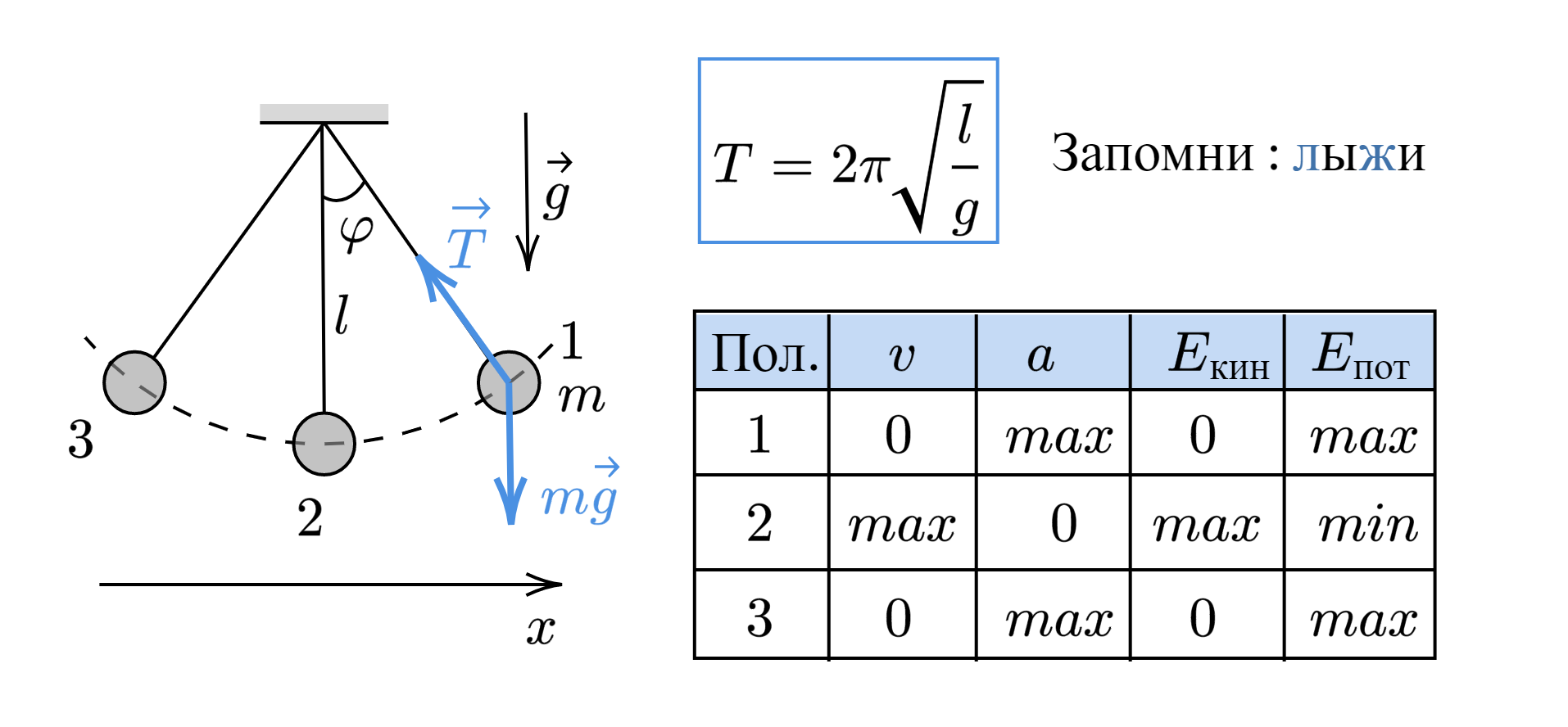
Найдём период малых колебаний математического маятника. Длина нити равна $l$ . Сопротивлением воздуха пренебрегаем. Запишем для маятника второй закон Ньютона:

m⃗a = m ⃗g+ ⃗T

и спроектируем его на ось X:

max = Tx

Если маятник занимает такое положение, как на рисунке (т.е. $x > 0$ ), то

x Tx = − T sin φ = − T l

Если же маятник находится по другую сторону от положения равновесия (т.е. $x < 0$ ), то

T = T sinφ = − T x x l

Итак, при любом положении маятника имеем

x- max = − T l

Когда маятник покоится в положении равновесия, выполнено равенство
$T = mg$ . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство $T ≈ mg$ . Воспользуемся им в предыдущей формуле:

x- max = − mg l

или

x ax = − g-l

Это уравнение гармонических колебаний, в котором

2 g ω = l

Отсюда и из соотношения $2π T = --- ω$ находим период математического маятника

|------∘---| |T = 2π l | ---------g-|

Превращение энергии при гармонических колебаниях

При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия — это энергия упругих деформаций пружины. Для математического маятника — это энергия в поле тяготения Земли.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д. Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Предыдущая справка

Следующая справка