Оптика

Основы геометрической оптики

Запоминайте формулы по каждой теме

Осваивайте новые концепции ежедневно

Вдумывайтесь в теоретические материалы

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела: Оптика

Теоретическая справка

#971

Понятие геометрической оптики

Геометрическая оптика изучает законы распространения света в прозрачных средах, отражения света от зеркально-отражающих поверхностей и принципы построения изображений при прохождении света в оптических системах без учета его волновых свойств. В рамках геометрической оптики свет распространяется как луч. Все законы геометрической оптики могут быть выведены из одного постулата, который называется принципом Ферма.

Принцип Ферма: свет всегда стремится попасть из одной точки в другую за экстремальное — наибольшее или наименьшее — время.

Как правило, в рамках школьной программы рассматриваются оптические системы, которые соответствуют только второму случаю. С учетом этого можно упростить данный принцип и свести его к следующему: «Свет всегда стремится попасть из одной точки в другую за наименьшее время».

Обратите внимание, что в задачах ЕГЭ чаще всего нужно опираться не на сам принцип Ферма, а на законы, которые из него следуют. Рассмотрим эти законы.

Законы геометрической оптики

1. Закон о прямолинейном распространении света: в однородной прозрачной среде свет распространяется прямолинейно.

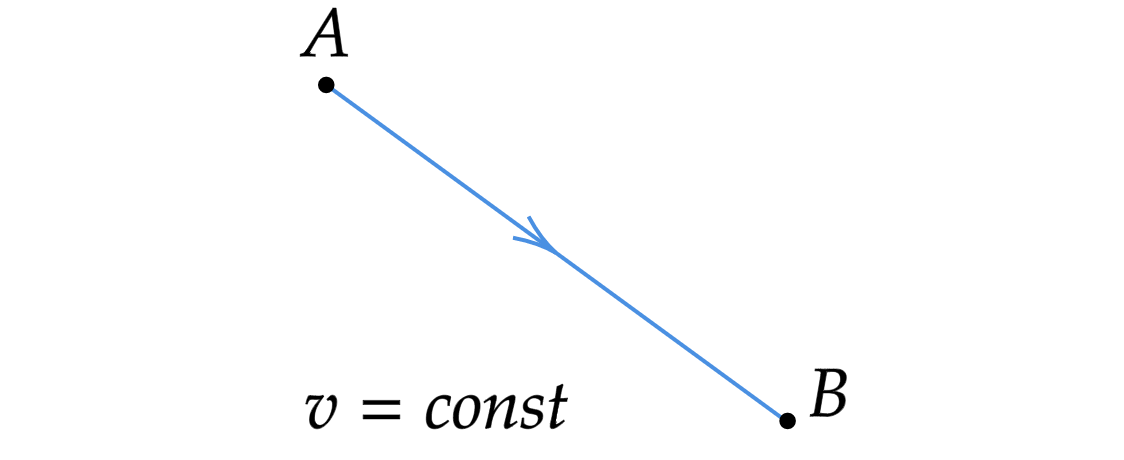
В однородной прозрачной среде свет распространяется с постоянной скоростью. Чтобы попасть из точки $A$ в точку $B$ за наименьшее время (исходя из принципа Ферма), свету необходимо распространяться прямолинейно.

2. Законы отражения:

1) При отражении падающий луч, отраженный луч и перпендикуляр к границе раздела двух сред, проведенный в точке падения луча, лежат в одной плоскости.

2) Угол отражения равен углу падения.

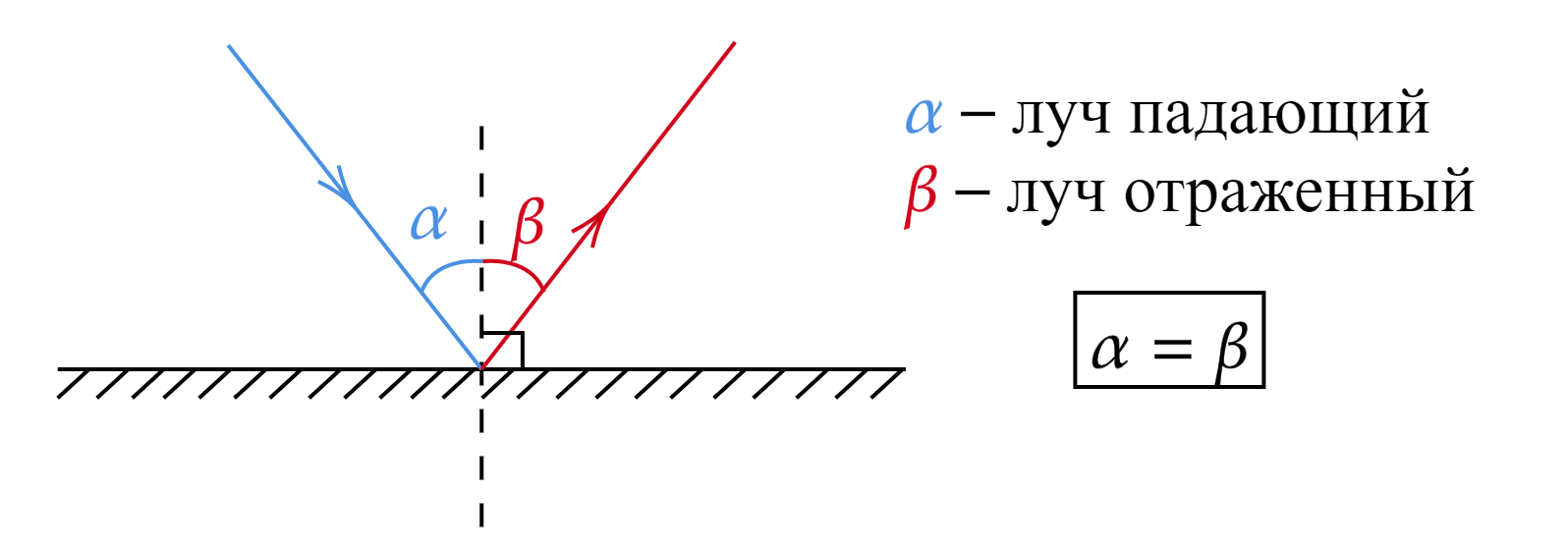
Обратите внимание, что углом падения называется угол между падающим лучом и перпендикуляром к поверхности. Углом отражения называется угол между отраженным лучом и перпендикуляром к поверхности.

3. Закон преломления (Закон Снеллиуса)

Соотношение между углами падения, преломления и абсолютными показателями преломления сред:

|---------------| n1sinα-=-n2sin-γ--

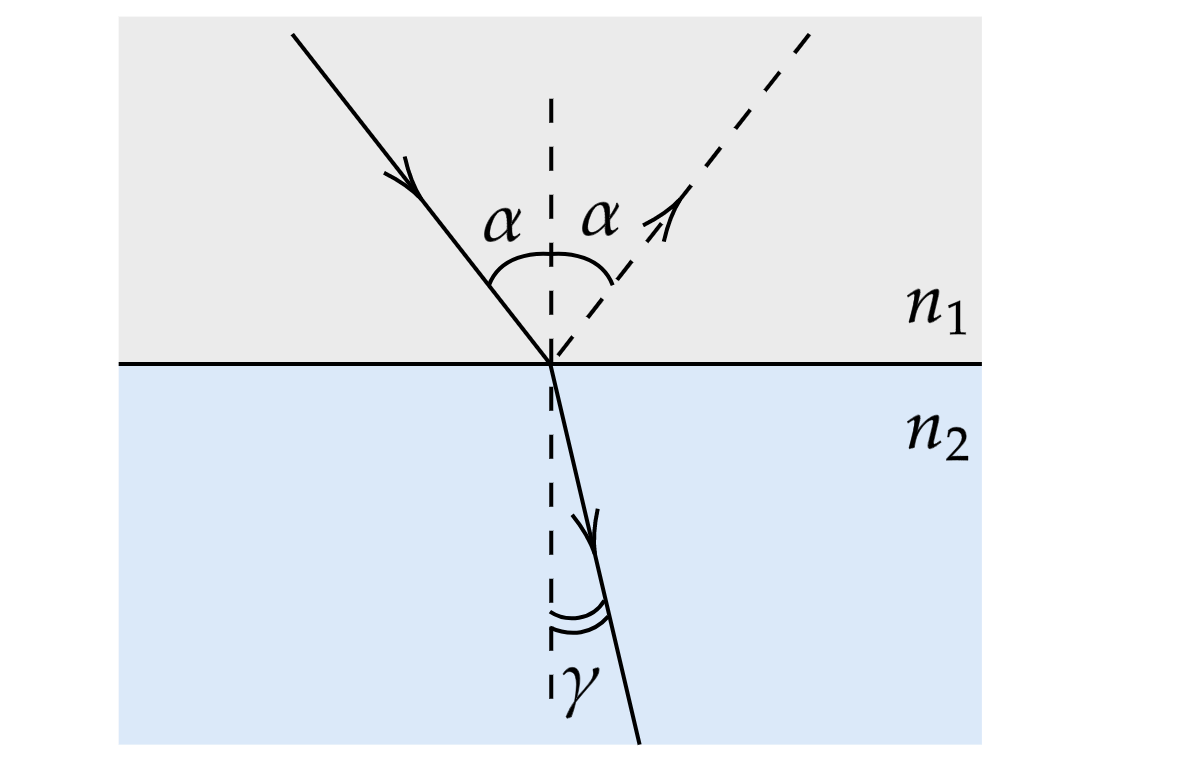
Абсолютный показатель преломления

В вакууме свет распространяется со скоростью $c = 3⋅108$ м/c. В любой другой среде свет распространяется со скоростью меньшей, чем в вакууме. Чтобы показать, во сколько раз изменяется его скорость, в физике вводят величину, которая называется абсолютным показателем преломления. Физический смысл абсолютного показателя преломления — отношение скорости распространения света $c$ в вакууме к его скорости $v$ в данной среде:

|----c-| |n = v | -------

Абсолютный показатель преломления всегда больше или равен 1: $n ≥ 1$ . Для воздуха принято $nвозд = 1$ , то есть в воздухе свет распространяется с той же скоростью $c = 3⋅108$ м/с, что и в вакууме.

Относительный показатель преломления

Относительный показатель преломления двух сред — это отношение абсолютных показателей преломления данных сред:

|------| n = n2 | ----n1--

Частные случаи для закона Снеллиуса

Переход из оптически менее плотной среды в оптически более плотную среду

$PIC$

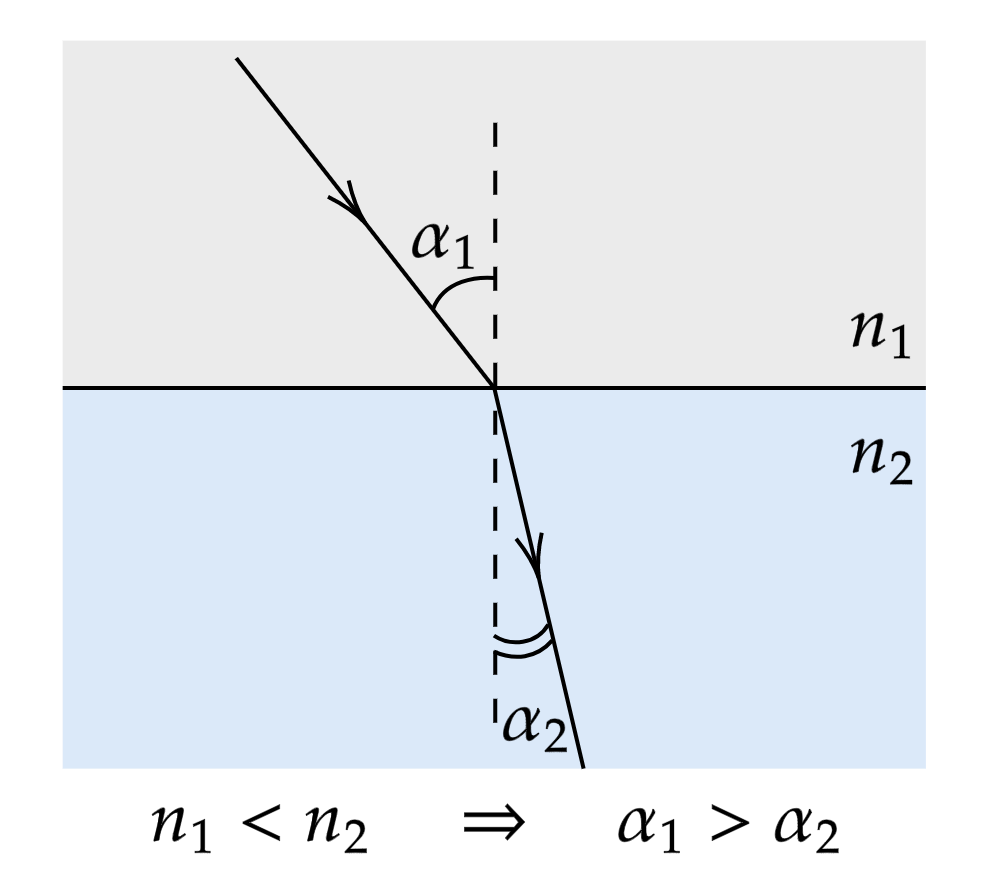
При $n1 < n2$ закон Снеллиуса $n1sinα1 = n2sin α2$ выполняется, если:
$sinα1 > sinα2$
Функция синуса возрастает от 0 до 90 градусов. То есть чем больше угол $α$ , тем больше его синус $sinα$ , поэтому
$α1 > α2$
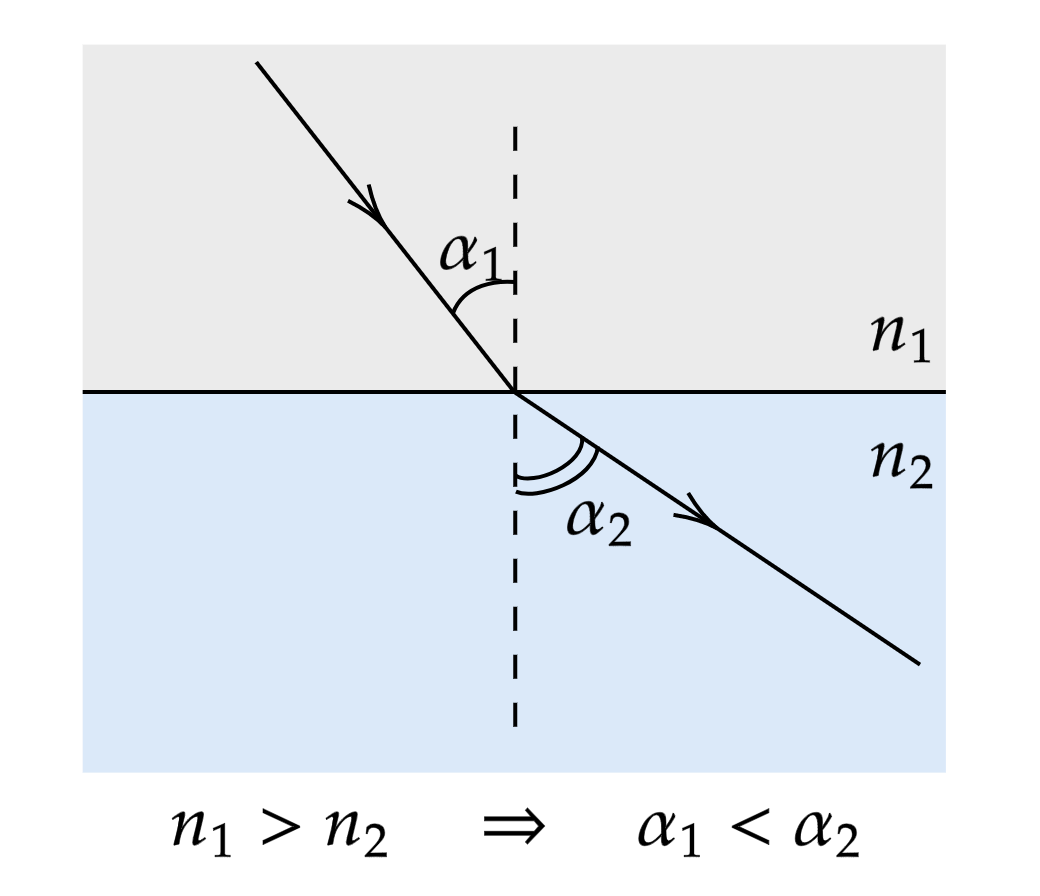
При переходе из оптически менее плотной среды в оптически более плотную среду угол преломления меньше угла падения.
Переход из оптически более плотной среды в оптически менее плотную среду

$PIC$

При $n1 > n2$ закон Снеллиуса $n1sinα1 = n2sin α2$ выполняется, если:
$sinα < sinα 1 2$
Функция синуса возрастает от 0 до 90 градусов. То есть чем больше угол $α$ , тем больше его синус $sinα$ , поэтому
$α1 < α2$
При переходе из оптически более плотной среды в оптически менее плотную среду угол преломления больше угла падения.
Луч падает перпендикулярно поверхности раздела сред

$PIC$

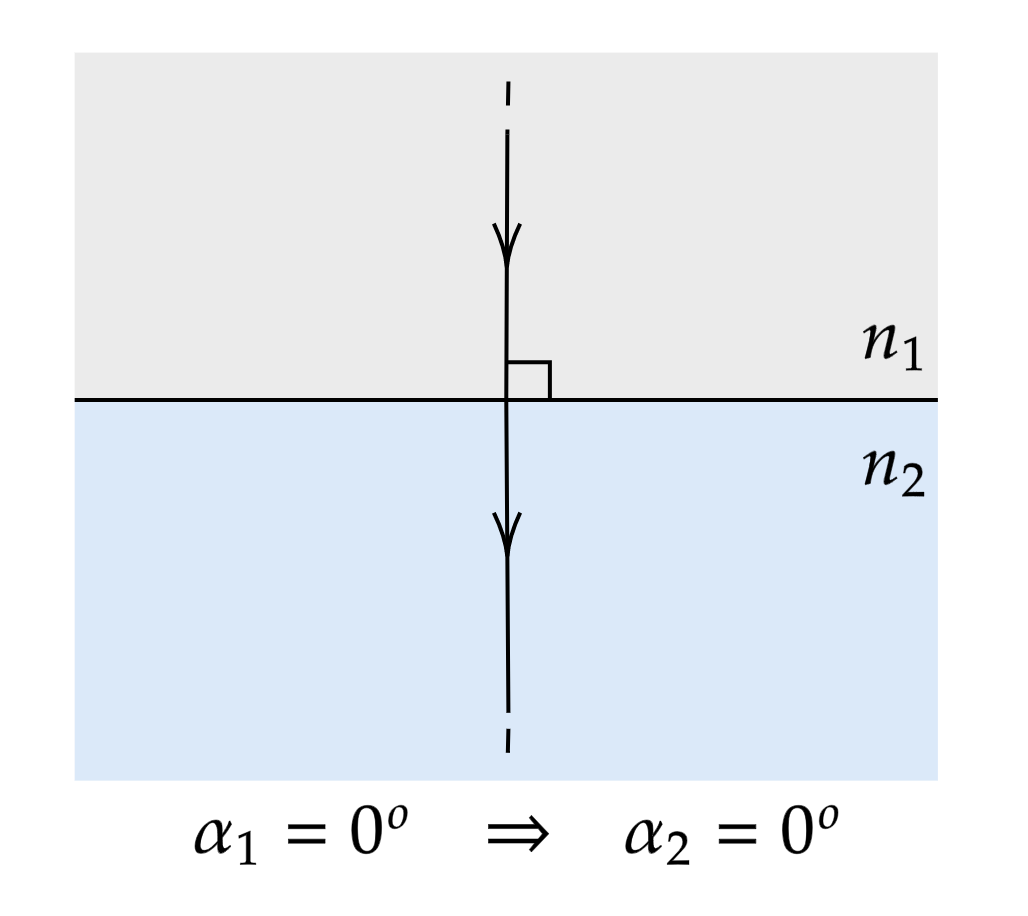
Угол между падающим лучом и перпендикуляром к поверхности равен 0 $o$ , то есть угол падения $α1 = 0o$ . Запишем закон Снеллиуса для этого случая:
$o n1 sin0 = n2sin α2$

$n ⋅0 = n sinα 1 2 2$
Чтобы закон выполнялся, синус угла преломления $sinα2$ также должен быть равен нулю, а значит и сам угол $α2$ должен быть равен нулю. Из этих рассуждений можно сделать вывод, что луч, падающий перпендикулярно границе раздела двух сред, не преломляется.

Полное внутреннее отражение

В законе полного внутреннего отражения рассматривается ситуация, когда свет переходит из оптически более плотной среды $n1$ в оптически менее плотную среду $n2$ . Для $n1 > n2$ угол преломления, как известно из частных случаев для закона Снеллиуса, больше угла падения. Если постепенно увеличивать угол падения при переходе света в оптически менее плотную среду, то угол преломления также будет увеличиваться.

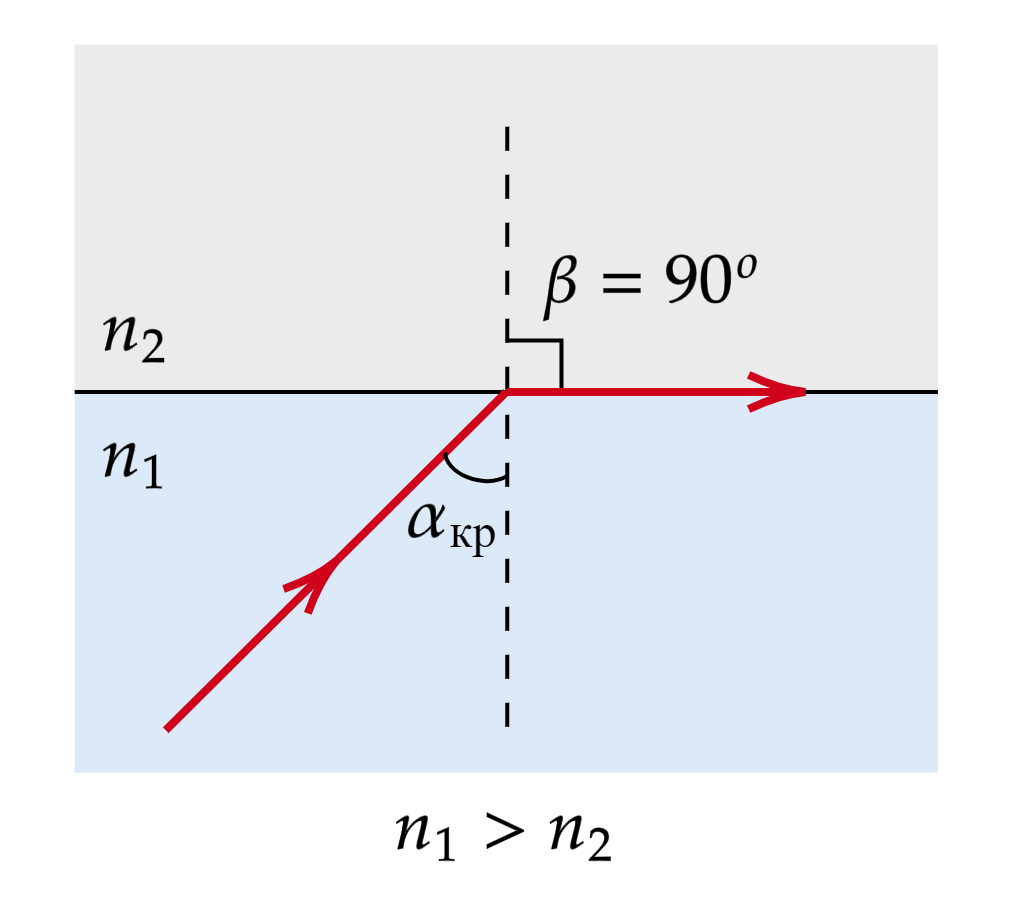
При некотором (критическом) значении угла падения $αкр$ угол преломления станет равен 90 $o$ .

Луч идет из среды $n 1$ под углом $α кр$ и выходит в среду $n 2$ под углом преломления, равным 90 $o$ . С учетом этого запишем закон Снеллиуса:

o o n1sin αкр = n2sin90 , причем sin90 = 1

n sinα = n 1 кр 2

Отсюда закон полного внутреннего отражения:

|----------| sinα = n2| ----кр---n1-

При углах падения больше критического $αкр$ преломленного луча не существует.

Закон Снеллиуса: вывод через принцип Ферма

Пусть имеется точка $A$ и точка $B$ . Примем, что в первой среде $n1$ свет распространяется со скоростью $v1$ , а во второй $n2$ — со скоростью $v2$ . По принципу Ферма свет попадает из точки $A$ в точку $B$ за наименьшее время.

Время распространения луча из точки $A$ в точку $B$ складывается из времени прохождения отрезка $AO$ и времени прохождения отрезка $OB$ :

t(x ) = AO + OB-- v1 v2

Пусть мы точно знаем положение точек $A$ и $B$ , то есть расстояния $h$ , $H$ и $L$ фиксированы. По теореме Пифагора из прямоугольных треугольников можно сделать замены для $OA$ и $OB$ :

√ -2---2- ∘H2--+-(L-−-x)2 t(x) =--h-+-x- + -------------- v1 v2

Чтобы найти минимальное время, найдем производную от функции времени $t(x )$ по $x$ (все остальные величины воспринимаем как константы, то есть как некоторые числа) и приравняем ее к нулю:

′ 1 1 1 1 t(x) = v1-⋅2√h2-+-x2-⋅2x + v2 ⋅2∘H2--+-(L-−-x)2 ⋅2(L − x )⋅(− 1) = 0

1- ----x---- 1- ----L-−-x----- v1 ⋅√ h2 + x2 = v2 ⋅ ∘ H2 +(L − x)2

Еще раз вспомним теорему Пифагора и сделаем обратные замены:

1-⋅-x- = -1 ⋅ L−-x- v1 AO v2 OB

Заметим, что отношения $x AO-$ и $L− x OB---$ из геометрического определения синуса (отношение противолежащего катета к гипотенузе) можно заменить как $sin α1$ и $sinα2$ соответственно: