12.09 Поиск наибольшего/наименьшего значения у произведения
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции
1) Найдем производную:
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна
или не существует):
(так как при любом
и на этот множитель можно поделить обе части уравнения).
Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства :

3) Эскиз графика :
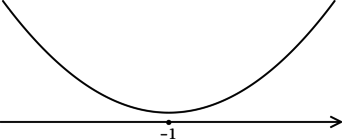
Таким образом, — точка минимума и наименьшее значение функции
равно
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции
1) Найдем производную:
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна 0 или не существует):
2) Найдём промежутки знакопостоянства и промежутки монотонности
:

3) Эскиз графика :
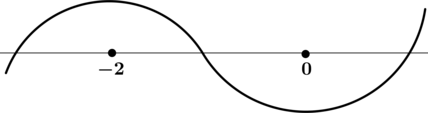
По полученному эскизу нельзя сказать наверняка, действительно ли в точке локального минимума
значение функции наименьшее, или же при каком-то отрицательном
значение функции
окажется меньше, чем при
. Найдём
:
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции на отрезке
Функция определена при всех Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем
ее производную:
Найдем нули производной:
Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:
При производная отрицательна, то есть функция
убывает. При
производная
положительна, то есть функция возрастает. Следовательно, наименьшее значение функция принимает в точке
Ошибка.
Попробуйте повторить позже
Найдите наибольшее значение функции
на отрезке
Функция определена при всех . Исследуем функцию и найдем ее промежутки возрастания и убывания, для этого найдем ее
производную:
Найдем нули производной:
Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков:
При производная положительна, то есть функция
возрастает; при
производная отрицательна, то есть
функция убывает. Следовательно, наибольшее значение функция принимает в точке
, и оно равно
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции .
1) .
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :

3) Эскиз графика :
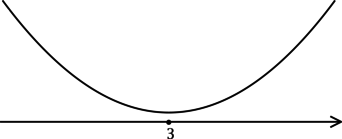
Таким образом, – точка минимума функции
.
,
Итого: наименьшее значение функции равно
.
Ошибка.
Попробуйте повторить позже
Найдите наибольшее значение функции .
1) .
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :
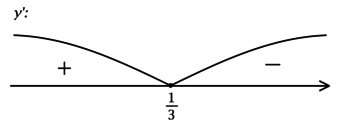
3) Эскиз графика :
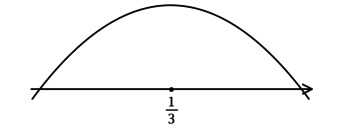
Таким образом, – точка максимума функции
.
,
Итого: наибольшее значение функции равно
.
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции .
1) .
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :

3) Эскиз графика :

Таким образом, – точка минимума функции
.
,
Итого: наименьшее значение функции равно
.
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции на отрезке
1) Найдем производную:
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна 0 или не существует):
Отсюда находим корни
Таким образом,
Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства и промежутки монотонности
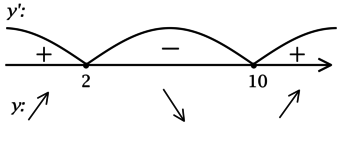
3) Найдём промежутки знакопостоянства и промежутки монотонности
на отрезке
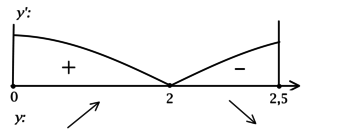
4) Эскиз графика на отрезке
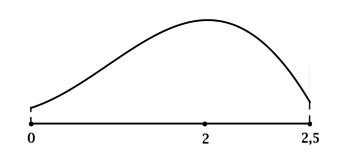
Таким образом, — точка локального максимума функции
и наименьшего значение на отрезке
функция
достигает в точке
или в точке
Сравним значения функции в этих точках:
Так как то
Тогда наименьшее значение функции на отрезке
равно 34.
Ошибка.
Попробуйте повторить позже
Найдите наибольшее значение функции .
1) .
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :

3) Эскиз графика :

Таким образом, – точка максимума функции
.
,
Итого: наибольшее значение функции равно
.
Ошибка.
Попробуйте повторить позже
Найдите наибольшее значение функции
Для того, чтобы найти наибольшее значение функции на отрезке, нужно схематично изобразить график
функции.
Для этого найдем производную:
Отметим нули на вещественной прямой и найдем знаки производной:

Следовательно, схематично график функции выглядит следующим образом:

Следовательно, наибольшее значение на отрезке
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции
на отрезке
Найдем критические точки заданной функции, для этого вычислим её производную:
Далее найдем нули производной:
Так как при любом вещественном
то критическими являются точки
Но точка не входит в отрезок
. Тогда для того, чтобы определить наименьшее значение функции
на данном отрезке, нужно сравнить значения функции в критической точке и на концах отрезка:
Значит, наименьшее значение функции на отрезке равно .
Ошибка.
Попробуйте повторить позже
Найдите наибольшее значение функции на отрезке
.
Анализируя производную на отрезке , видно, что
—
единственная точка экстремума, причём при
производная
отрицательная, а при
производная положительная. Тогда
— точка максимума функции на отрезке. Тогда наименьшее значение
функции на отрезке равно
.
Ошибка.
Попробуйте повторить позже
Найдите наибольшее значение функции на отрезке
Функция определена при всех Найдем промежутки возрастания/убывания
функции, для этого вычислим ее производную:
Таким образом, производная при всех
следовательно, функция
возрастает на
и на
то есть возрастает на отрезке
Следовательно, наибольшее значение функция принимает в точке
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции на отрезке
Исследуем функцию на области определения Найдем ее производную:
Нули производной:
Нули производной и точки, в которых она не существует, разбивают область определения производной на промежутки, на каждом из которых она непрерывна и принимает значения одного знака. Найдем знаки производной на каждом из таких промежутков.
Таким образом, — точка минимума и в ней функция принимает свое
наименьшее значение:
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции на
.
ОДЗ: . Решим на ОДЗ:
Заметим, что - просто число, тогда
1) .
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :
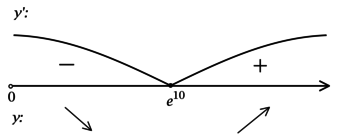
3) Найдём промежутки знакопостоянства на рассматриваемом отрезке
:

4) Эскиз графика на отрезке :
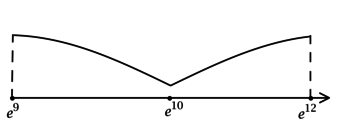
Таким образом, - точка минимума функции
на
и наименьшее значение функция
достигает в ней.
.
Итого: – наименьшее значение функции
на
.
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение функции на отрезке
.
1)
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
2) Найдём промежутки знакопостоянства :
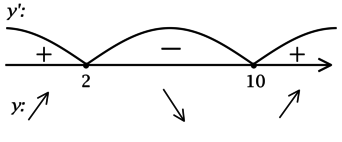
3) Найдём промежутки знакопостоянства на рассматриваемом отрезке
:

4) Эскиз графика на отрезке :
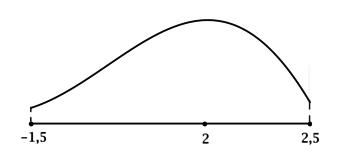
Таким образом, наименьшее значение на отрезке функция
достигает или в
,
или в
. Сравним эти значения:
,
.
Остаётся сравнить данные значения: так как , то
. Итого:
– наименьшее значение функции
на отрезке
.



