04 Законы сохранения в механике - Каталог заданий по ЕГЭ

Ошибка.
Попробуйте повторить позже

Задача 81#96069Максимум баллов за задание: 4

Пластилиновый шарик в момент $t = 0$ бросают с горизонтальной поверхности земли с некоторой начальной скоростью под углом $α$ к горизонту. Одновременно с некоторой высоты над поверхностью земли начинает падать из состояния покоя другой такой же шарик. Шарики абсолютно неупруго сталкиваются в воздухе. Сразу после столкновения скорость шариков направлена горизонтально. В момент времени $τ$ шарики падают на землю. Какова начальная скорость $⃗v0$ шарика, брошенного под углом к горизонту? Сопротивлением воздуха пренебречь.

Источники: Демидова 2019

Показать ответ и решение

Обоснование
Инерциальную систему отсчета свяжем с Землей. Шарики будем считать материальными точками, поскольку их размерами в условиях задачи можно пренебречь. Так как сопротивление воздуха не учитывается, то шарики до и после столкновения находятся в свободном падении и можно использовать формулы кинематики для тела, брошенного под углом к горизонту, и для тела, падающего вертикально. Для абсолютно неупругого столкновения шариков можно использовать закон сохранения импульса, так как время столкновения мало и действием внешней силы тяжести за это время можно пренебречь.

Решение
1. Первый шарик начинает движение из начала координат, а второй – из точки А. До и после столкновения (в точке В) шарики свободно падают. Поэтому до столкновения для первого шарика

y (t)= v t− gt2= v sin αt− gt2, 1 0y 2 0 2

v1y(t) =v0sinα− gt,

а для второго шарика

v2y(t)= −gt.

2. Шарики сталкиваются в момент $t1$ , при этом импульс системы двух шариков сохраняется: $m ⃗v1+ m⃗v2 = 2m ⃗u0$ , а скорость $⃗u0$ шариков после удара согласно условию горизонтальна. Поэтому $v1y(t1)+ v2y(t1) = 0$ , или $(v0sinα − gt1)+ (− gt1)= 0$ , откуда $t1 = v0s2ingα.$
3. Столкновение шариков происходит на высоте

gt2 v2sin2α v2sin2α 3 v2sin2α h= y1(t1)= v0sin α⋅t1− 21-= -02g---− -08g---= 8 ⋅-0g---.

4. Поскольку скорость шариков после удара горизонтальна, интервал времени $t2$ от столкновения шариков до их падения на землю находится из условия $h = gt22- 2$ , откуда $t = ∘ 2h= √3-⋅ v0sinα. 2 g 2g$

5. Шарики упадут на Землю в момент

v0sinα √ - τ = t1 +t2 =-2g-- ⋅(1+ 3)

6. Выразим начальную скорость:

v0 = ---2gτ-√--- sinα(1+ 3)

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 82#96197Максимум баллов за задание: 4

От груза, неподвижно висящего на невесомой пружине жёсткостью $k,$ отделился с начальной скоростью, равной нулю, его фрагмент массой $m = 0,6 кг.$ После этого при возникших колебаниях оставшаяся часть груза поднималась на максимальную высоту $h = 3 см$ относительно первоначального положения. Какова жесткость пружины?

Источники: Демидова 2019

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Кубик массой $M$ и $m$ имеет малые размеры по сравнению с пружиной и движутся поступательно, поэтому описываем кубики моделью материальной точки. Так как тела являются материальными точками, то описывать их движение в ИСО будем с помощью второго закона Ньютона

3. Так как изменения механической энергии тела в ИСО равно работе всех непотенциальных сил, приложенных к телу, а в данном случае таких сил нет, (сопротивлением воздуха пренебрегаем, трения нет) полная механическая энергия кубика при его движении сохраняется.

4. Так как деформации упругие, то применим закон Гука для нахождения силы упругости, действующей на тело во время возникших колебаний.

Решение В начальном положении тело находилось в равновесии, то есть сила тяжести уравновешивает силу Гука

⃗FН +(M + m )⃗g = 0,

где $FН = ky0$ – сила Гука. Или в проекции на ось $x$

(m + M )g = ky0 (1)

Так как начальная скорость куска $m$ равна нулю, то и скорость $M$ после отделения также равна нулю. После отделения части груза, будут совершаться гармонические колебания, значит по закону сохранения энергии

2 2 ky20 = k(y0−2-h)-+ Mgh

Раскроем скобки

ky2 k(y2− 2y0h +h2) kh -20= ---0---2------ +Mgh ⇒ ky0 =-2 +Mg (2)

kh+ Mg = mg + Mg ⇒ mg = kh 2 2

Отсюда

2mg- 2-⋅0,6⋅10 k = h = 0,03 = 400 Н/м

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 83#96377Максимум баллов за задание: 4

Снаряд, движущийся со скоростью $⃗v0,$ разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину $ΔE.$ Скорость осколка, движущегося вперёд по направлению движения снаряда, равна $v1.$ Найдите массу $m$ осколка.

Источники: Демидова 2019

Показать ответ и решение

Обоснование

Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью Земли. Будем считать все тела материальными точками. Трением снаряда и осколков о воздух пренебрежём.

Поскольку время разрыва снаряда мало, импульсом внешних сил (сил тяжести) можно пренебречь, а значит, для решения задачи можно воспользоваться законом сохранения импульса.

Так как при решении задачи мы пренебрегаем силой трения, то можно использовать закон сохранения энергии для снаряда с учётом энергии разрыва.

Решение

Кинетическая энергия тела находится по формуле:

2 Ek = mv-, 2

где $m$ – масса тела, $v$ – его скорость.

Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения энергии

( 2 2 2 |{ 2mv0-+ ΔE = mv1-+ mv2- |( 2 2 2 2mv0 = mv1 − mv2

где $v0$ начальная скорость гранаты.

Выразим начальную скорость гранаты из второго уравнения.

v0 = v1−-v2 2

Подставим в первое уравнение системы

2m-(v1-− v2)2+ ΔE = mv21+ mv22 4⋅2 2 2

Выразим изменение кинетической энергии за счет взрыва

m-(2v21-+2v22 −-v21 +-2v1v2−-v22) m-(v1+v2)2 ΔE = 4 = 4

Выразим искомую массу:

4ΔE m = (v-+-v)2 1 2

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 84#98910Максимум баллов за задание: 4

От груза, неподвижно висящего на невесомой пружине жёсткостью $k =400 Н/м,$ без начальной скорости отделился его фрагмент массой $600 г.$ На какую максимальную высоту относительно первоначального положения поднялась оставшаяся часть груза? Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.

Источники: Резервная волна 2024

Показать ответ и решение

Обоснование

1. Введем инерциальную систему отсчета (ИСО) связанную с Землей.

2. Кубик массой $M$ и $m$ имеет малые размеры по сравнению с пружиной и движутся поступательно, поэтому описываем кубики моделью материальной точки. Так как тела являются материальными точками, то описывать их движение в ИСО будем с помощью второго закона Ньютона

3. Так как изменения механической энергии тела в ИСО равно работе всех непотенциальных сил, приложенных к телу, а в данном случае таких сил нет, (сопротивлением воздуха пренебрегаем, трения нет) полная механическая энергия кубика при его движении сохраняется.

4. Так как деформации упругие, то применим закон Гука для нахождения силы упругости, действующей на тело во время возникших колебаний.

Решение

$PIC$

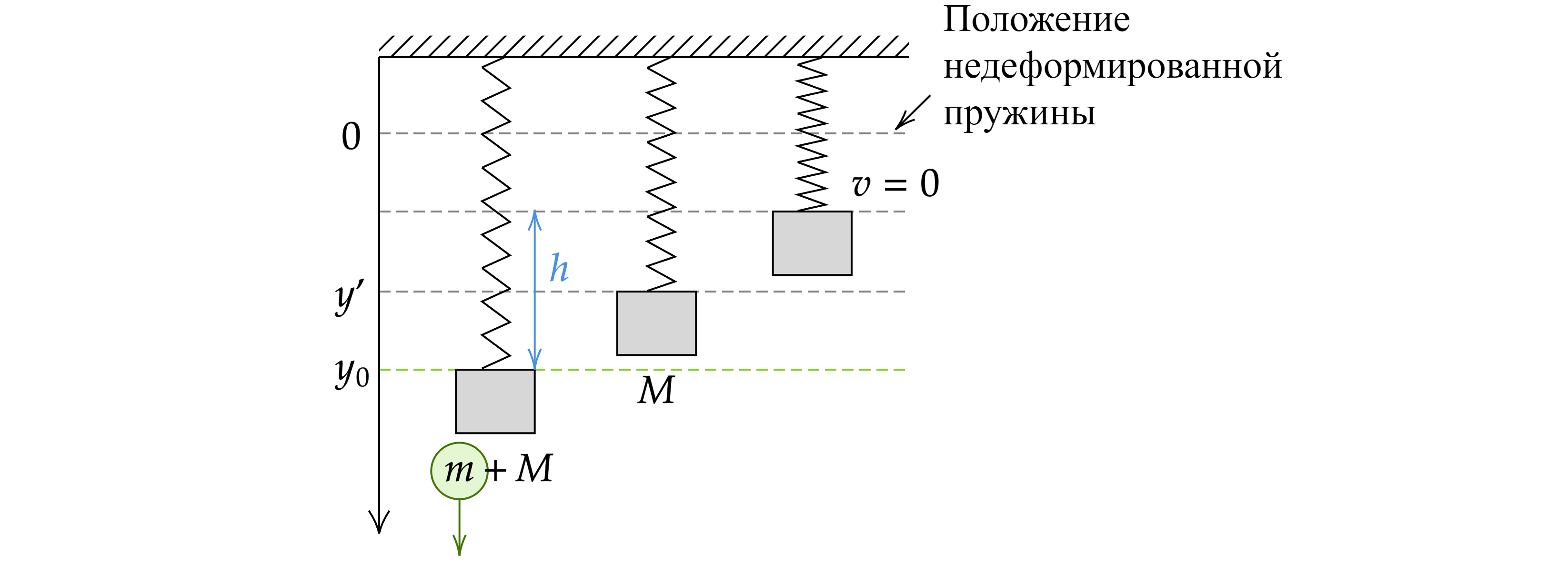
В начальном положении тело находилось в равновесии, то есть сила тяжести уравновешивает силу Гука

⃗FН +(M + m )⃗g = 0,

где $FН = ky0$ – сила Гука. Или в проекции на ось $x$

(m + M )g = ky0 (1)

Так как начальная скорость куска $m$ равна нулю, то и скорость $M$ после отделения также равна нулю. После отделения части груза, будут совершаться гармонические колебания, значит по закону сохранения энергии

2 2 ky0 = k(y0−-h)-+ Mgh 2 2

Раскроем скобки

ky20= k(y20 −-2y0h-+h2) +Mgh ⇒ ky0 = kh +Mg (2) 2 2 2

kh kh 2 + Mg = mg + Mg ⇒ mg = 2

Отсюда

2mg 2⋅0,6⋅10 h = -k--= ---400--- =0,03 м = 3 см

Ответ:

2mg h = -k--= 3 см

Критерии оценки


Критерии оценивания выполнения задачи	Баллы

Критерий 1

Верно обоснована возможность испольования законов	1
(закономерностей). В данном случае: выбор ИСО, модель материальной точки, использование закона Гука, использование второго закона Ньютона, использование закона сохранения энергии

В обосновании возможности использования законов	0
(закономерностей) допущена ошибка
ИЛИ
Обоснование отсутствует

Критерий 2
Приведено полное решение, включающее следующие элементы:	3
I) записаны положения теории и физические законы,
закономерности, применение которых необходимо для решения
задачи выбранным способом (в данном случае - закон Гука, второй закон Ньютона, закон сохранения механической энергии, формула потенциальной энергии упруго деформированного тела);
II) описаны вновь вводимые в решении буквенные обозначения
физических величин (за исключением обозначений констант,
указанных в варианте КИМ, обозначений величин, используемых
в условии задачи, и стандартных обозначений величин,
используемых при написании физических законов);
III) проведены необходимые математические преобразования
и расчёты (подстановка числовых данных в конечную формулу),
приводящие к правильному числовому ответу (допускается решение
«по частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения
фиизческой величины

Правильно записаны все необходимые положения теории,	2
фиизческие законы, закономерности, и проведены необходимые
преобразования, но имеется один или несколько из следующих
недостатков.

Записи, соответствующие пункту II, представлены не в полном
объёме или отсутствуют.
И(ИЛИ)
В решении имеются лишние записы, не входящие в решение
(возможно, неверные), которые не отделены от решения и не
зачёркнуты
И(ИЛИ)
В необходимых математических преобразованиях или вычислениях
допущены ошибки, и(или) в математических преобразованиях/
вычислениях пропущены логически важные шаги.
И(ИЛИ)
Отсутствует пункт IV, или в нём допущена ошибка (в том числе
в записи единиц измерений величины)

Представлены записи, соответствующие одному из следующих	1
случаев.
Представлены только положения и формулы, выражающие
физические законы, применение которых необходимо для решения
данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
ИЛИ
В решении отсутствует ОДНА из исходных формул, необходимая
для решения данной задачи (или утверждение, лежащее в основе
решения), но присутствуют логически верные преобразования
с имеющимися формулами, направленные на решение задачи.
ИЛИ
В ОДНОЙ из исходных формул, необходимых для решения данной
задачи (или в утверждения, лежащем в основе решения), допущена
ошибка, но присутствуют логически верные преобразования
с имеющимися формулами, направленные на решение задачи

Все случаи решения, которые не соответствуют вышеуказанным	0
критериям выставления оценок в 1, 2, 3 балла

Максимальный балл	4

Ошибка.
Попробуйте повторить позже

Задача 85#114520Максимум баллов за задание: 4

Снаряд массой $2m = 8$ кг разрывается на одинаковых осколка, один из которых продолжает лететь в том же направлении со скоростью $v1 = 10$ м/с, а другой движется в противоположную сторону со скоростью $v2 = 5$ м/с. В момент взрыва кинетическая энергия осколков увеличивается за счет взрыва на $ΔE$ . Найдите $ΔE$ . Сопротивлением воздуха пренебречь. Какие законы Вы используете для решения задачи? Обоснуйте их применение.

Показать ответ и решение

Обоснование
1) Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью Земли.
2) Будем считать все тела материальными точками. Трением снаряда и осколков о воздух пренебрежём.
3) Поскольку время разрыва снаряда мало, импульсом внешних сил (сил тяжести) можно пренебречь, а значит, для решения задачи можно воспользоваться законом сохранения импульса.
4) Так как при решении задачи мы пренебрегаем силой трения, то можно использовать закон сохранения энергии для снаряда с учётом энергии разрыва.

Решение
Кинетическая энергия тела находится по формуле:

E = mv2-, k 2

где $m$ – масса тела, $v$ – его скорость.
Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения энергии

( 2 2 2 |{ 2mv0-+ ΔE = mv1-+ mv2- | 2 2 2 ( 2mv0 = mv1 − mv2

где $v0$ начальная скорость гранаты.
Выразим начальную скорость гранаты из второго уравнения.

v1−-v2 v0 = 2

Подставим в первое уравнение системы

2m (v − v )2 mv2 mv2 ----14⋅2-2--+ ΔE = -2-1+ -2-2

Выразим изменение кинетической энергии за счет взрыва

2 2 2 2 2 2 ΔE = m-(2v1 +-2v2 −-v1 +-2v1v2−-v2)= m-(v1-+v2)-= 4-кг(10-м/с+-5 м/с)-= 225 Д ж 4 4 4

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 86#125666Максимум баллов за задание: 4

Пластилиновый шарик в момент $t= 0 с$ бросают с горизонтальной поверхности земли с некоторой начальной скоростью под углом $α = 30∘$ к горизонту. Одновременно с некоторой высоты над поверхностью земли начинает падать из состояния покоя другой такой же шарик. Спустя время $τ = 1 с$ шарики абсолютно неупруго сталкиваются в воздухе. Сразу после столкновения скорость шариков направлена горизонтально. Какова начальная скорость $v0$ шарика, брошенного под углом к горизонту? Сопротивлением воздуха пренебречь. Какие законы Вы использовали для описания движения? Обоснуйте их применение к данному случаю.

Источники: основная волна 2024

Показать ответ и решение

Обоснование

1. Выберем Землю как инерциальную систему отсчета, используемые законы будем записывать в этой СО.

2. Движение тел поступательное, поэтому будем считать их материальными точками.

3. В условии данной задачи пренебрегаем силой сопротивления воздуха, поэтому тела движутся только под действитем силы тяжести с ускорением свободного падения, направленным вертикально вниз. Ось Oy направлена вертикально вверх.

4. В условиях данной задачи проекция ускорения на ось Ox равна 0, поэтому описывать движение по горизонтали будем с помощью законов прямолинейного равномерного движения. Проекция на ось Oy равна $− g,$ поэтому описывать движение по вертикали будем с помощью законов прямолинейного равноускоренного движения.

5. Соударение происходит мгновенно и убсолютно неупруго, значит можно использовать закон сохранения импульса для описания соударения тел.

Решение

$PIC$

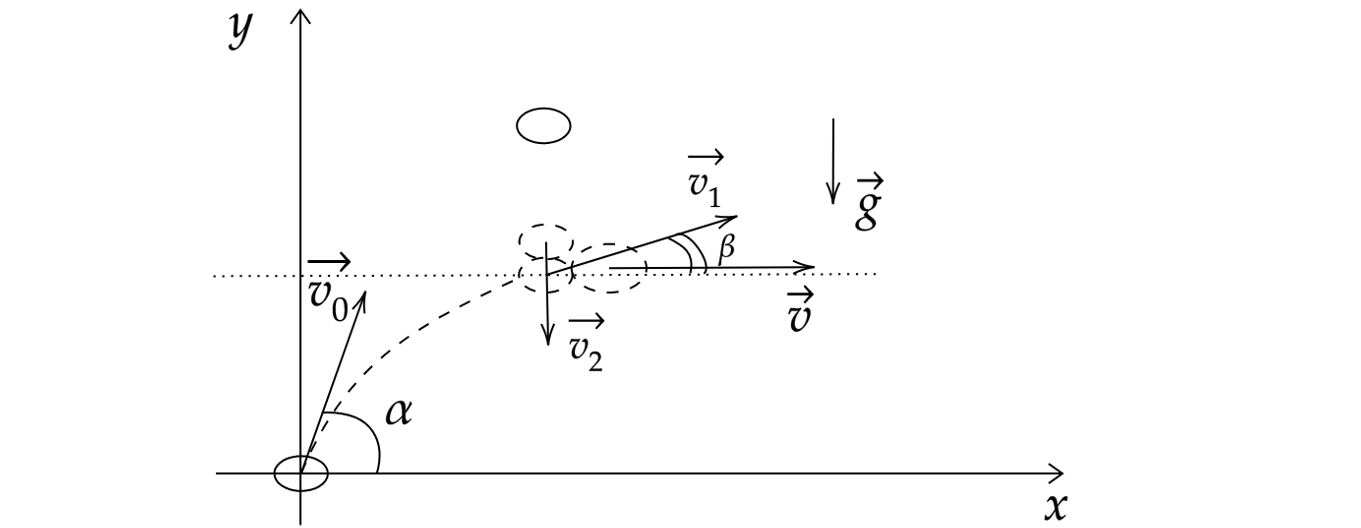
Уравнение скорости шарика

⃗v1 = ⃗v0+ ⃗at

где $v1$ - скорость шарика, $v0$ - начальная скорость шарика, $a$ - ускорение шарика.
Спроецируем уравнение скорости шарика, летевшего с Земли через время $τ$ (относительно оси Oy):

vsinβ = v0 sinα − gτ

где $β$ - угол, на который наклонена скорость этого шарика относительно горизонта спустя время $τ$ .
Спроецируем уравнение скорости второго шарика через время $τ$ (относительно оси Oy):

− v2 = gτ

Пусть массы шариков равны $m.$ По закону сохранения импульса:

mv⃗1+ m ⃗v2 = 2m⃗v

Относительно оси Oy:

mv1 sinβ− mv2 = 0

v1sin β = v2

v0sinα − gτ = gτ

2gτ 2 ⋅10 ⋅1 v0 = sinα-= --0,5--= 40 м/с

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 87#136813Максимум баллов за задание: 4

Снаряд в полёте разорвался на два равных осколка, один из которых продолжил лететь по направлению движения снаряда, а другой полетел в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков возросла за счёт энергии взрыва на величину 0,5 МДж. Модуль скорости осколка, летящего по направлению движения снаряда, равен 900 м/с, а модуль скорости второго осколка равен 100 м/с. Найдите массу снаряда. Сопротивлением воздуха и массой порохового заряда пренебречь.

Источники: Демоверсия 2026

Показать ответ и решение

Обоснование
1) Задачу будем решать в инерциальной системе отсчёта, связанной с поверхностью Земли.
2) Будем считать все тела материальными точками. Трением снаряда и осколков о воздух пренебрежём.
3) Поскольку время разрыва снаряда мало, импульсом внешних сил (сил тяжести) можно пренебречь, а значит, для решения задачи можно воспользоваться законом сохранения импульса.
4) Так как при решении задачи мы пренебрегаем силой трения, то можно использовать закон сохранения энергии для снаряда с учётом энергии разрыва.

Решение

Кинетическая энергия осколка находится по формуле:

E = mv2-, k 2

где $m$ – масса осколка, $v$ – его скорость.
Запишем систему уравнений, состоящую из закона сохранения импульса и закона сохранения энергии

( 2 2 2 |{ 2mv0-+ ΔE = mv1-+ mv2- | 2 2 2 ( 2mv0 = mv1 − mv2

где $v0$ начальная скорость снаряда.
Выразим начальную скорость гранаты из второго уравнения.

v1−-v2 v0 = 2

Подставим в первое уравнение системы

2m (v − v )2 mv2 mv2 ----14⋅2-2--+ ΔE = -2-1+ -2-2

Выразим массу снаряда $M = 2m$ :

2 2 2 2 ΔE = m-(2v1 +-2v2 −-v1 +-2v1v2−-v2) → m =--4ΔE--- → 4 (v1 +v2)2

8ΔE 8 ⋅0,5⋅106 → M = 2m = (v1+-v2)2 = (900+-100)2 = 4 кг

Ответ:

$--8ΔE--- M = (v1+ v2)2 = 4 кг$

Критерии оценки

Критерии проверки

Критерий 1

1 балл ставится если

Верно обоснована возможность использования законов (закономерностей). В данном случае: выбор ИСО, материальная точка, условия применения закона сохранения импульса и закона сохранения энергии

_________________________________________________________________________________________________________________________

В обосновании отсутствует один или несколько из элементов.

(ИЛИ)

В обосновании допущена ошибка.

(ИЛИ)

Обоснование отсутствует

Критерий 2

3 балла ставится если:

_________________________________________________________________________________________________________________
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: закон сохранения импульса, закон сохранения энергии);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых вусловии задачи, и стандартных обозначений величин, используемых при написании физических законов);
III) представлены необходимые математические преобразования и расчёты (подстановка числовых данных в конечную формулу), приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
IV) представлен правильный ответ с указанием единиц измерения физической величины

2 балла ставится если:

_________________________________________________________________________________________________________________
Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования, но имеется один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.

И (ИЛИ)

В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения и не зачёркнуты.

И (ИЛИ)

B необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.

И (ИЛИ)

Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины)

1 балл ставится если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.

ИЛИ

В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

ИЛИ

В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи

Во всех остальных случаях за задачу выставляется 0 баллов.