Преобразования плоскости
Ошибка.
Попробуйте повторить позже
Дед Мороз наколдовал на серединах сторон треугольника шестиконечные снежинки, как показано на рисунке:
![]()
(вершина треугольника и середина стороны треугольника берутся концами стороны соответствующего правильного шестиугольника)
Докажите, что на полученном новогоднем чуде точки пересечения медиан треугольников и
совпадают.
Пусть — произвольная точка плоскости.
Про точку пересечения медиан треугольника
известно, что:
(это характеристическое свойство следует из того, что точка пересечения медиан является центром масс )
А требуется доказать, что является ещё и точкой пересечения медиан треугольника
, то есть:
Левые части полученных двух векторных равенств совпадают, поэтому надо доказать про правые, что разность правых частей в этих равенствах равна нулевому вектору, то есть (преобразуем по правилу вычитания векторов):
Возьмём серединный треугольник и повернём его вокруг точки
на
. Получим треугольник
такой,
что
К тому же,
Значит,
Но тогда получаем требуемое:
Ошибка.
Попробуйте повторить позже
На сторонах и
треугольника
нашлись такие точки
и
отличные от вершин, что
и
Точка
симметрична точке
относительно прямой
Докажите, что
является биссектрисой угла
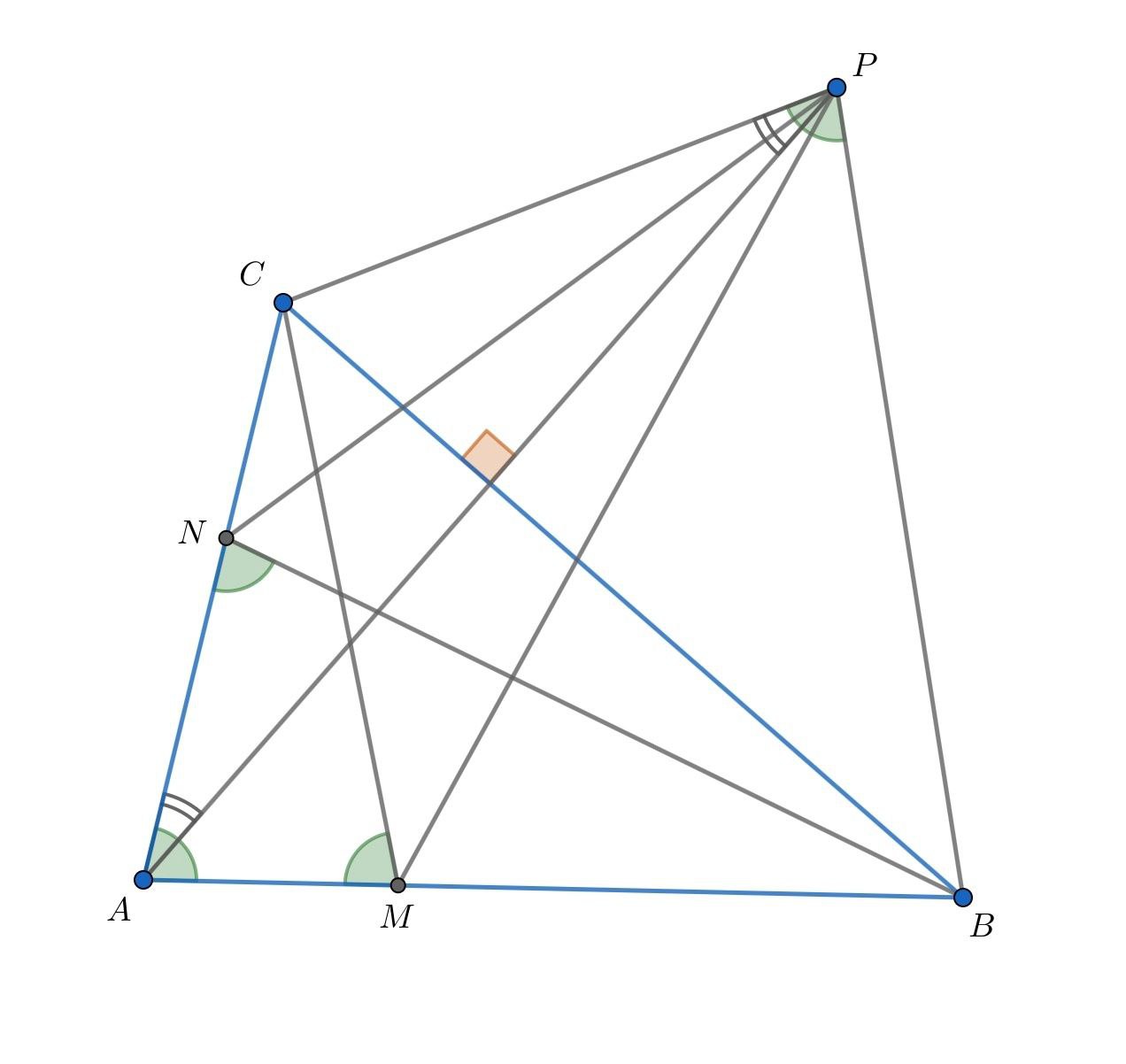
Из симметрии следует, что Отсюда
поэтому четырёхугольник — вписанный. Отсюда
Аналогично
Ошибка.
Попробуйте повторить позже
Диагонали четырехугольника пересекаются в
и
— в
и
— в
Через точку
проведена
прямая, параллельная
пересекающая противоположные стороны четырехугольника в точках
и
Докажите, что
Проективным преобразованием переведем прямую в бесконечно удаленную. После преобразования противоположные стороны
четырехугольника
параллельны, следовательно, он является параллелограммом.
![]()
Осталось заметить, что чевианы и
в треугольниках
и
образующие прямую параллельную
равны, т.к.
являются соответственными элементами в равных треугольниках, но двойное отношение
где
— бесконечно удаленная точка,
в которой пересекаются прямые, которые имеют то же направление, что и
равно
а, значит, было таковым и до преобразования,
следовательно,
являлось серединой отрезка
Ошибка.
Попробуйте повторить позже
Пусть два треугольника и
расположены таким образом, что прямые, соединяющие соответственные вершины,
конкуррентны, то три точки, в которых пересекаются, будучи продолжены, три соответственные стороны, коллинеарны.
Пусть прямые, соединяющие соответственные вершины треугольников и
пересекаются в точке
и
Переведем прямую
в бесконечно удаленную. После преобразования
и
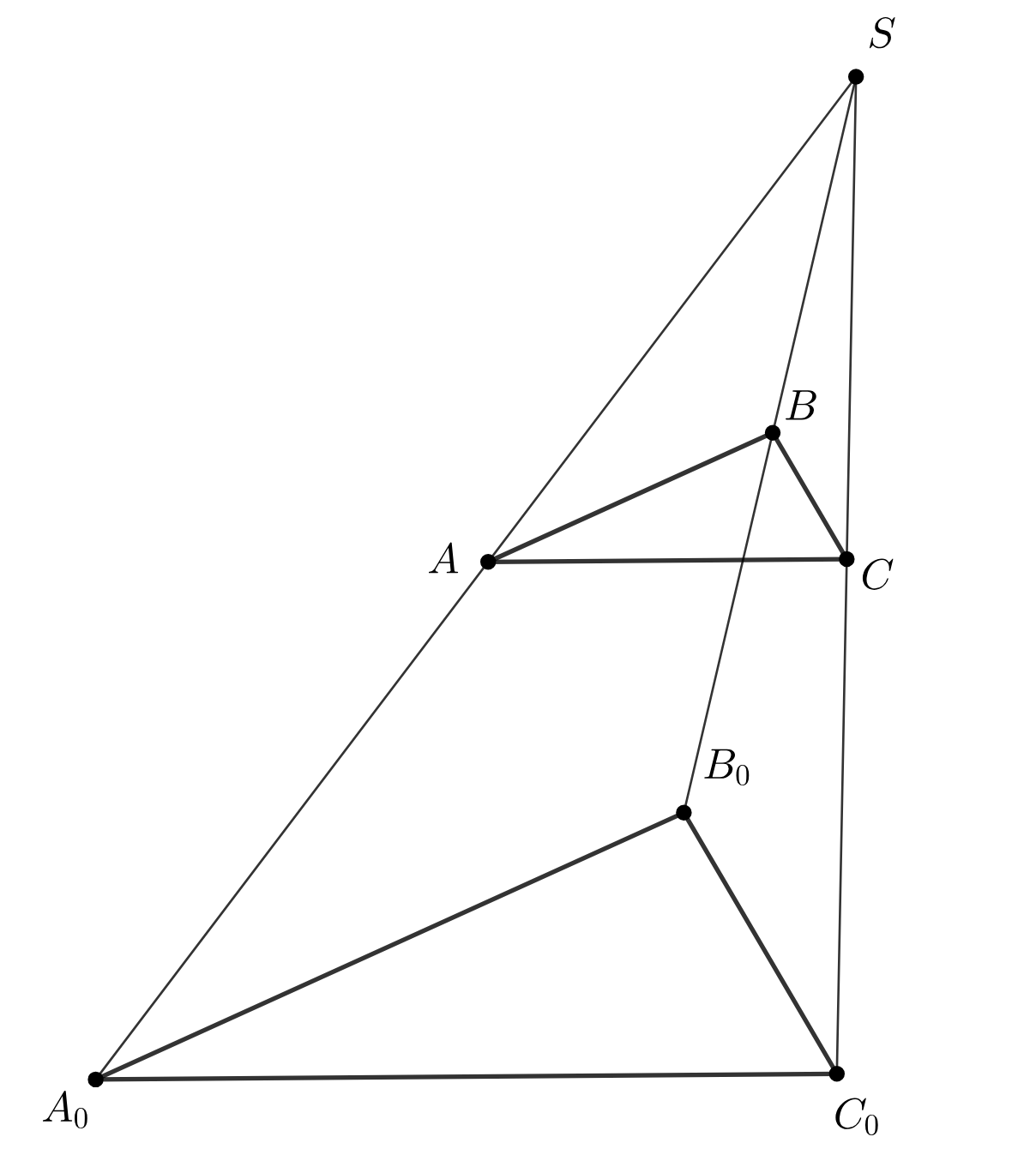
Рассмотрим гомотетию с центром в точке переводящая точку
в точку
она переведет прямую
в
следовательно,
точку
в
аналогично
в
а, значит, прямую
в прямую
что влечет их параллельность, тем самым они
пересекаются в бесконечно удаленной прямой, что доказывает коллинеарность точек
после преобразования, а, значит, и
коллинеарность до преобразования.
Замечание. Решение “по теореме Дезарга ч.т.д.” не засчитывается!
Ошибка.
Попробуйте повторить позже
Дан четырехугольник Пусть
и
Обозначим через
точки
Докажите, что
конкурентны.
Проективным преобразованием переведем в квадрат. Точки
и
перейдут в бесконечно удаленные. Заметим, что треугольники
и
равны и симметричны относително точки
, а, значит, прямые
и
параллельны и пересекаются на
бесконено удаленной прямой, тем самым их точка пересечения коллинеарна с точками
и
после преобразования, поскольку каждая
из них так же лежит на бесконечно удаленной прямой, что влечет кокурентность прямой
с данными —
и
.
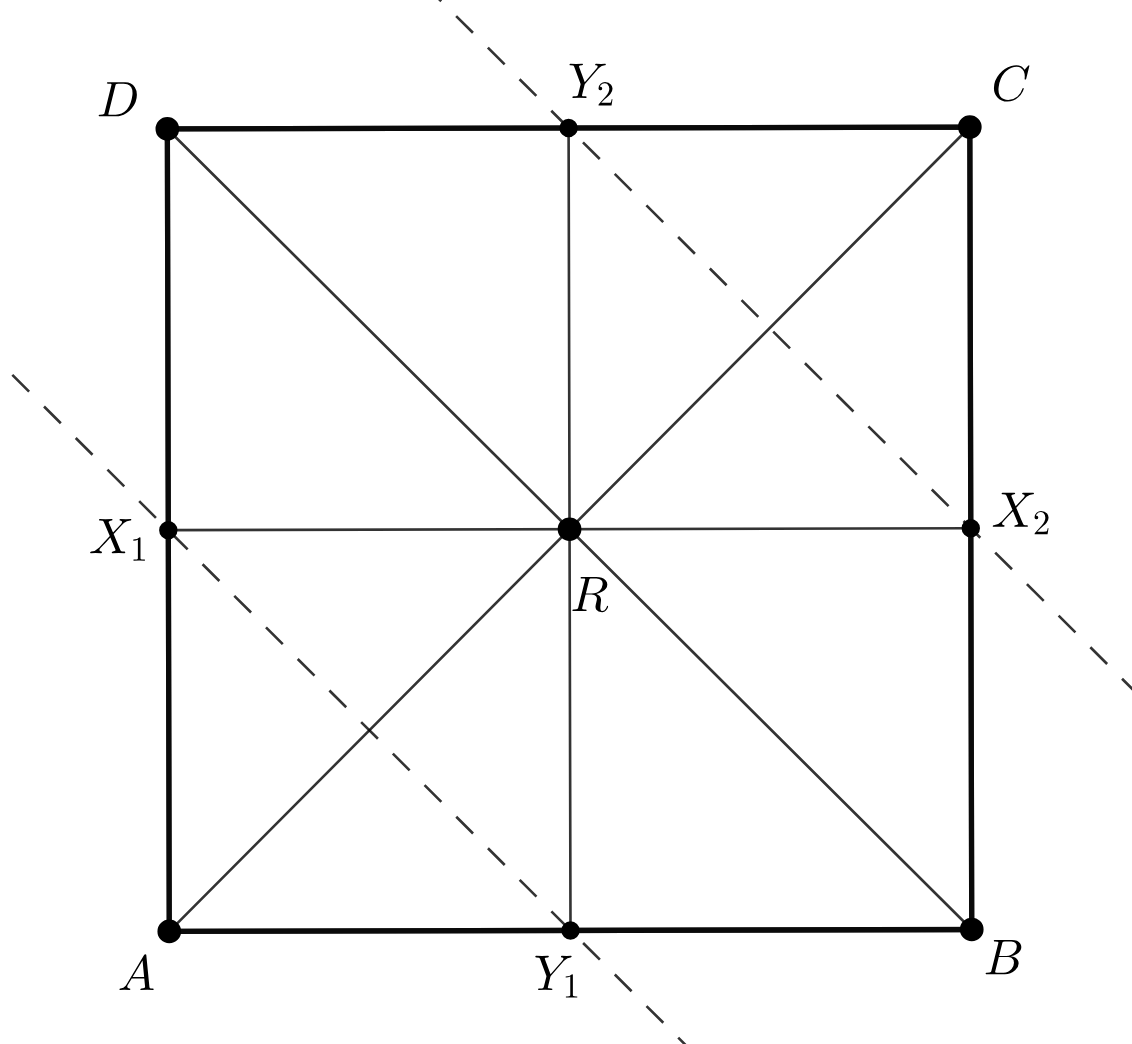
Замечание. Аналогично можно показать, что прямые конкурентны.
Ошибка.
Попробуйте повторить позже
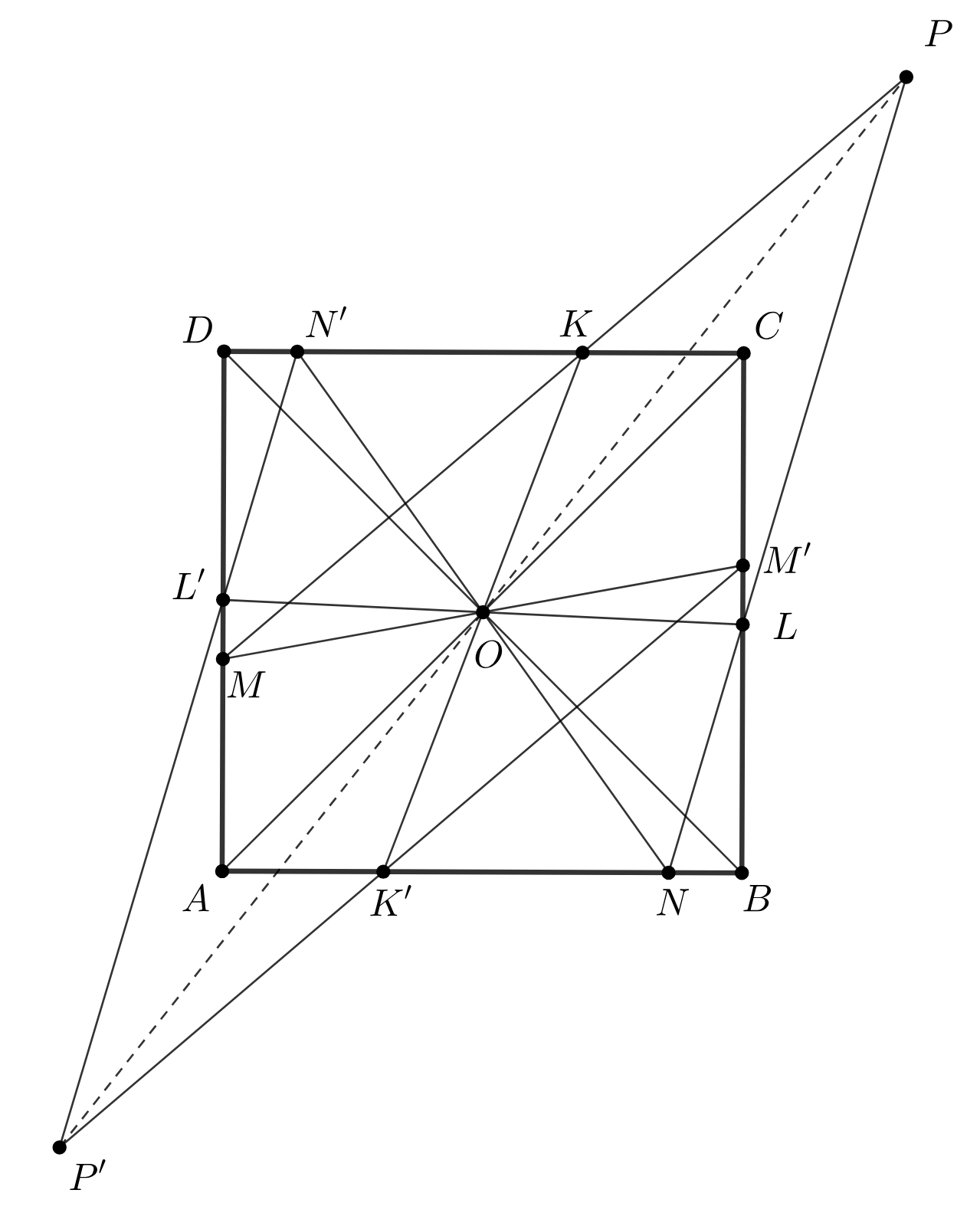
Через точку пересечения диагоналей четырехугольника проведены четыре прямые, пересекающие его противоположные стороны в
точках
и
и
и
и
(возможно много конфигураций). Прямые
и
и
пересекаются в точках
и
Докажите, что точки
лежат на одной прямой.
Проективным преобразованием переведем четырехугольник в квадрат. Рассмотрим симметрию относительно точки
Четверка точек
переходит в четверку точек
следовательно, прямая
переходит в
— в
тем самым, точка пересечения прямых
и
переходит в точку пересечения
и
а
значит точки
и
симметричны относительно
что доказывает их коллинеарность, а значит коллинеарность до
преобразования.
Ошибка.
Попробуйте повторить позже
Есть точки прямые
и
пересекаются в точке
прямые
и
пересекаются в точке
На плоскости взята
произвольная точка
точки
спроецированы на
с центром в
в результате чего получились точки
соответственно. Докажите, что
пересекаются в одной точке.
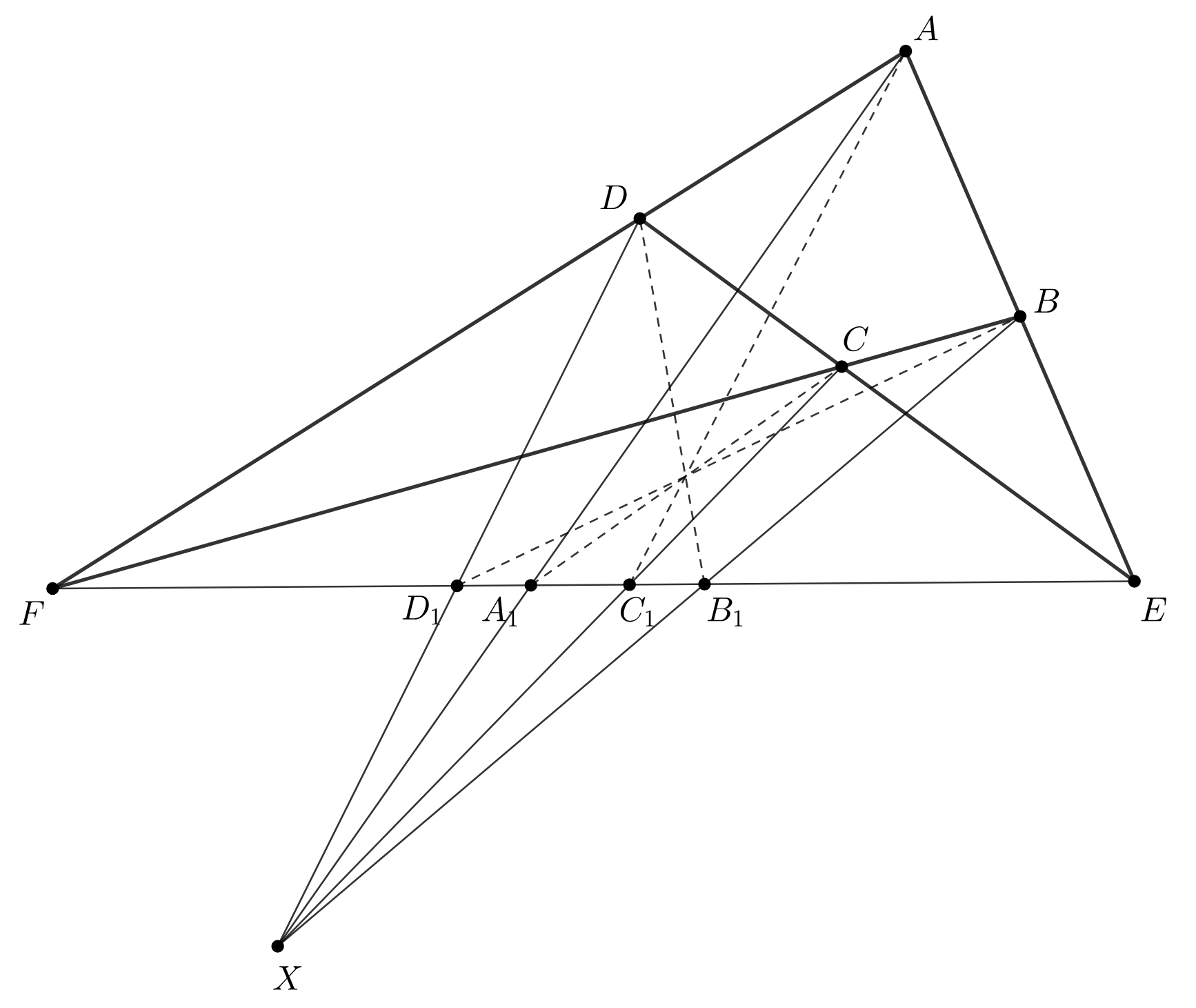
Проективным преобразованием переведем четырехугольник в квадрат. Прямая
при этом перейдет в бесконечно удаленную, а
значит каждая из точек
,
,
,
является бесконечно удаленной, а значит прямые
и
являются параллельными, т.к.
пересекаются в бесконечно удаленной точке
.
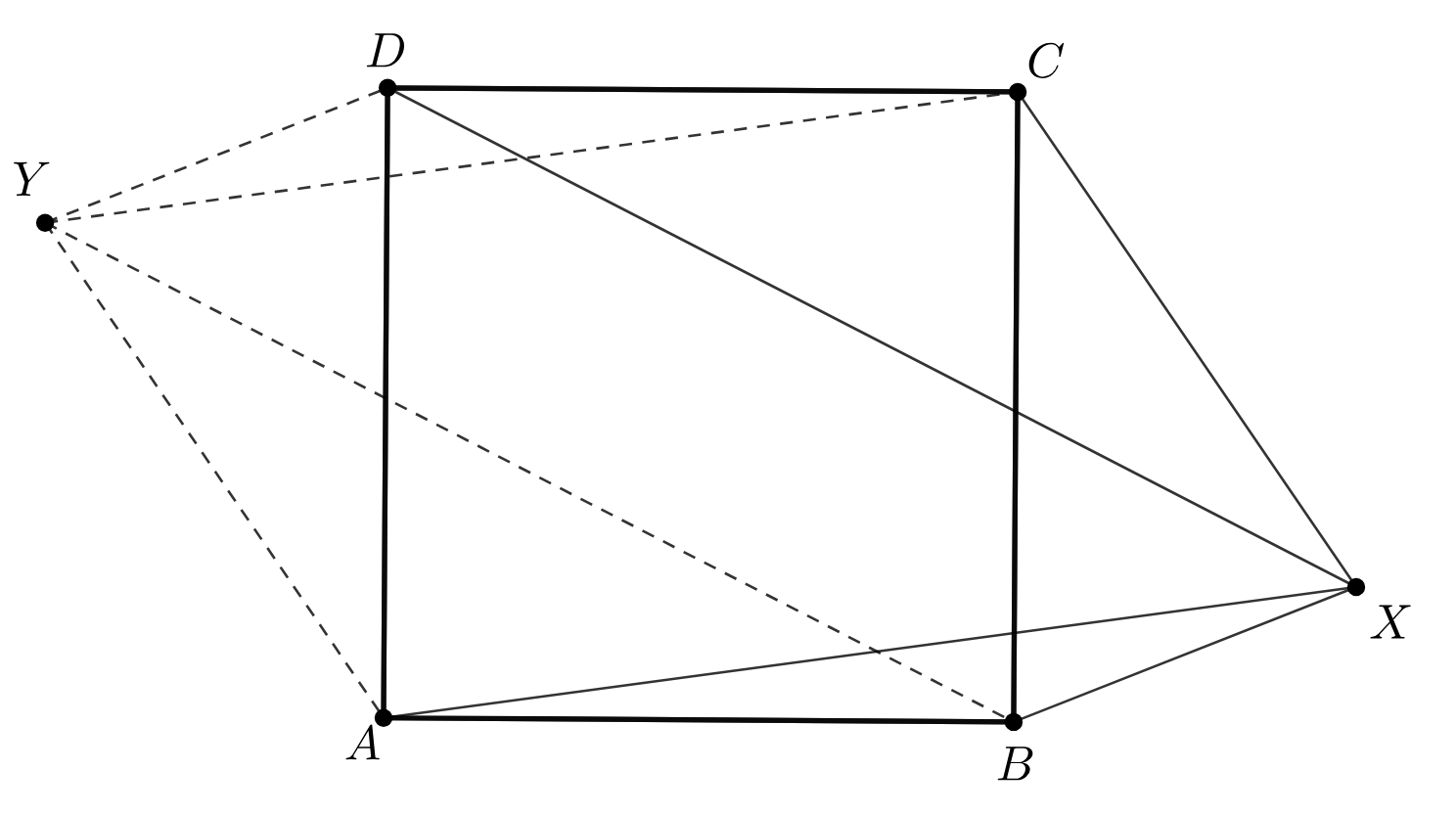
Рассмотрим симметрию относительно точки центра квадрата, тогда прямая
перейдет в прямую
, которая пройдет через
точку
, симметричную точки
относительно
. Аналогично, через точку
пройдут прямые
,
,
, что доказывает их
конкуррентность после преобразования, а значит и конкуррентность до преобразования.
Ошибка.
Попробуйте повторить позже
Докажите, что геометрическое место точек пересечения диагоналей четырехугольников у которых стороны
и
лежат на
двух данных прямых
и
а стороны
и
пересекаются в данной точке
является прямой, проходящей через точку
пересечения прямых
и
Рассмотрим задачу после проективного преобразования, которое переводит прямую в бесконечно удаленную. Прямые
фиксированы и параллельны. Стороны
и
так же параллельны, а значит
— параллелограмм, следовательно, точка
пересечения его диагоналей лежит на прямой, параллельной
и
равноудаленной от них, а значит не зависит от выбора точек
Точки пересечения диагоналей лежат на одной прямой после проективного преобразования, следовательно лежали на одной
прямой и до этого.
Ошибка.
Попробуйте повторить позже
Докажите, что для любого нечетного на плоскости можно указать
различных точек, не лежащих на одной прямой, и разбить их
на пары так, чтобы любая прямая, проходящая через две точки из разных пар, проходила бы еще через одну из этих
точек.
Пусть — правильный
-угольник,
— прямая, содержащая его сторону, противоположную вершине
— точка пересечения прямой
с бесконечно удаленной прямой. Разобьем точки
на пары
Покажем, что это разбиение обладает требуемым свойством. Для этого нужно рассмотреть прямые
п
![]()
Прямая
содержит все точки
Поскольку
среди них есть точка, отличная от
п
Прямая
параллельна одной из прямых
поскольку число
нечетно. Следовательно, прямая
проходит через точку
Если
то прямая, проходящая через вершину
параллельно прямой
содержит некоторую вершину
Поэтому
прямая
проходит через точку
Применив к набору точек проективное преобразование, можно добиться, чтобы все эти точки не были бесконечно
удаленными.
Ошибка.
Попробуйте повторить позже
Докажите, что прямые, соединяющие противоположные точки касания описанного четырехугольника, проходят через точку пересечения диагоналей.
Проективным преобразованием переведем точку пересечения прямых, соединяющих противоположные точки касания, в центр вписанной окружности. При этом преобразовании противоположные стороны четырехугольника перейдут в параллельные, следовательно, четырехугольник перейдет в параллелограмм. Поскольку существует вписанная в него окружность, то он является ромбом, для которого условия задачи очевидно, ведь в силу симметрии относительно центра вписанной окружности, диагонали проходят через центр окружности.
![]()
![]() Условие задачи до и после проективного преобразования.
Условие задачи до и после проективного преобразования.
Ошибка.
Попробуйте повторить позже
Через точку проводятся всевозможные пары секущих
и
окружности
(
— точки пересечения с окружностью).
Найдите геометрическое место точек пересечения прямых
и
Рассмотрим отдельно два случая.
Точка
лежит вне
Сделаем проективное преобразование, при котором окружность
перейдет в окружность, а точка
— в
бесконечно удаленную точку, т. е. образы всех прямых, проходящих через
будут друг другу параллельны. Тогда образом искомого ГМТ
является прямая
— их общий перпендикуляр, проходящий через центр окружности. (Для доказательства нужно воспользоваться
симметрией относительно прямой
) Следовательно, само искомое ГМТ есть прямая, проходящая через точки касания
с касательными,
проведенными через точку
![]()
Точка
лежит внутри
Сделаем проективное преобразование, при котором окружность
перейдет в окружность, а точка
— в ее центр. Тогда в обеих задачах образом искомого ГМТ является бесконечно удаленная прямая. Следовательно, само искомое ГМТ есть
прямая.
Замечание. Полученная прямая в обоих случаях совпадает с полярой точки относительно
Ошибка.
Попробуйте повторить позже
В окружность вписан шестиугольник
— точки пересечения пар прямых
и
и
и
и
Докажите, что если три из этих точек лежат на одной прямой, то и четвёртая точка лежит на этой
прямой.
Проведём проективное преобразование, сохраняющее окружность и переводящее точку в её центр. В результате
станет
прямоугольником, а прямая
— его осью симметрии. Если одна из точек
лежит на этой оси, то точки
и
симметричны
относительно неё, а значит, и вторая точка лежит на
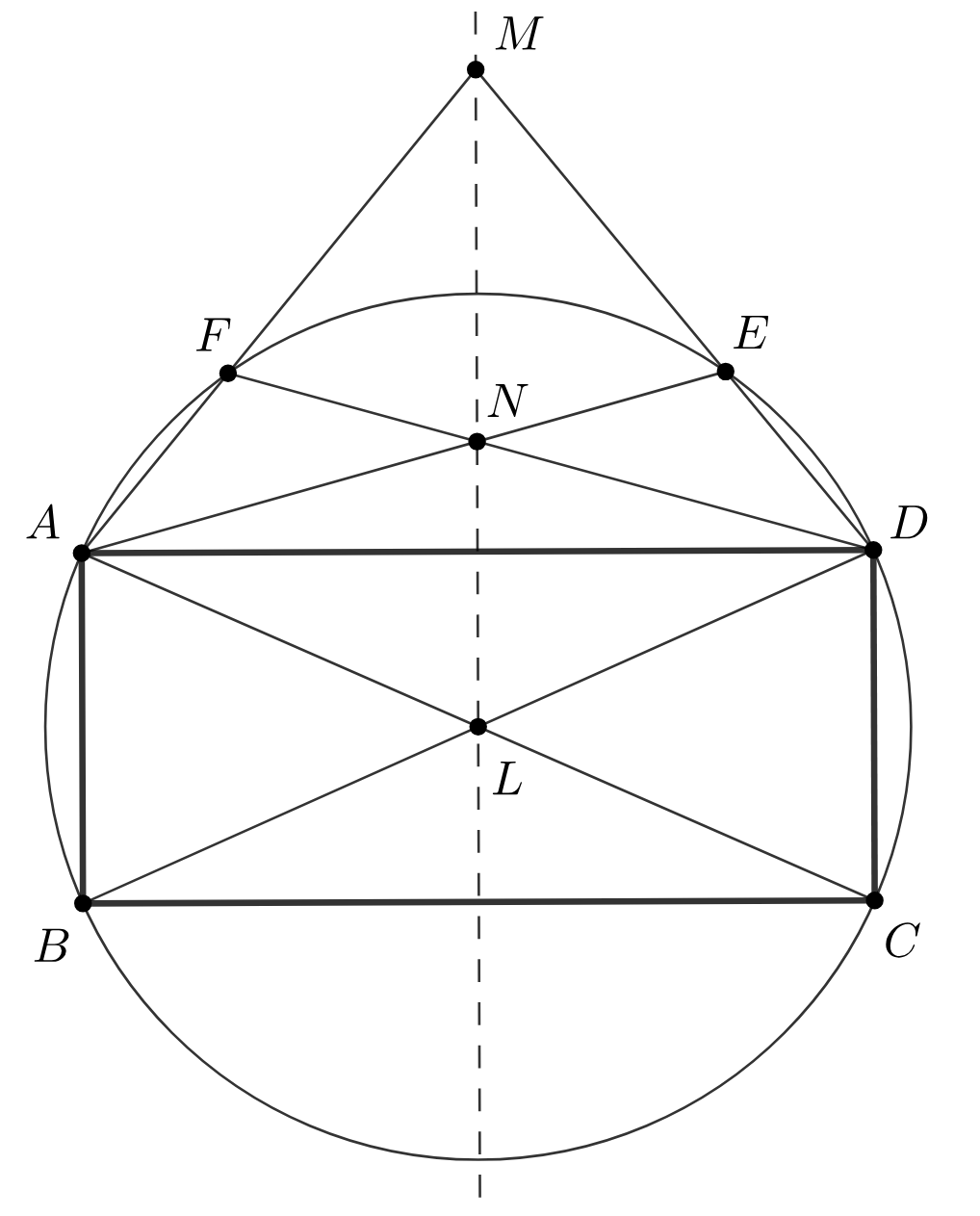
Ошибка.
Попробуйте повторить позже
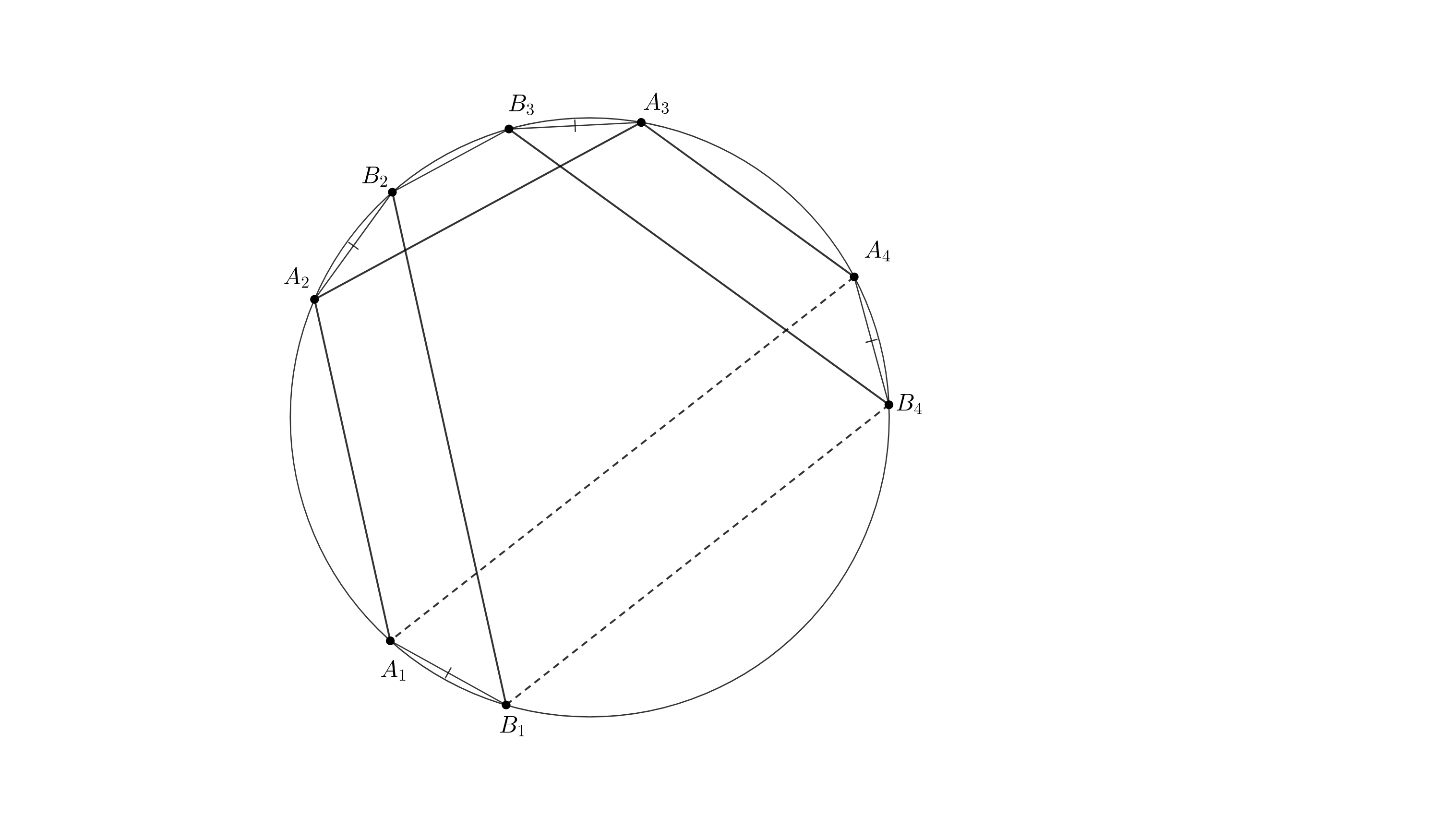
Теорема о двойной бабочке. На окружности отмечены точки
Прямая
пересекает прямые
в точках
соответственно и прямые
в точках
соответственно.
Докажите, что прямая
проходит через точку
![]()
Рассмотрим проективное преобразование, которое оставит на месте, а прямую
переведет в бесконечно удаленную.
При этом точка
так же перейдет в бесконечно удаленную. Следовательно, прямые для всех
верно, что
Покажем, что тогда
Действительно,
следовательно,
Аналогично,
Таким образом
следовательно
так же является бесконечно удаленной
точкой.
Ошибка.
Попробуйте повторить позже
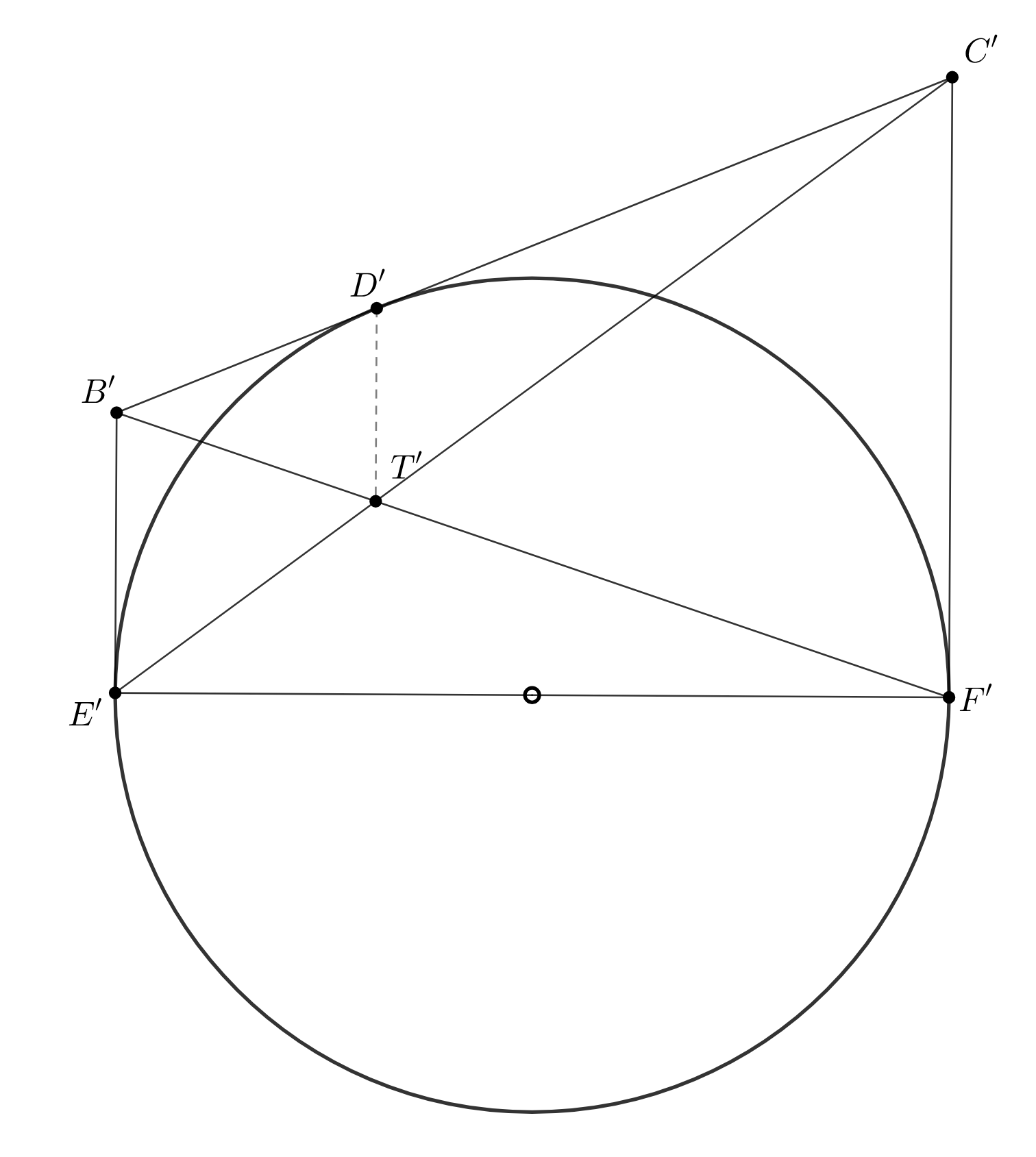
Вневписанная окружность треугольника касается стороны
в точке
а продолжений сторон
и
— в
точках
и
Пусть
— точка пересечения прямых
и
Докажите, что точки
и
лежат на одной
прямой.
Пусть — образы точек
при проективном преобразовании, которое вневписанную окружность треугольника
переводит в окружность, а хорду
в диаметр. Тогда
— бесконечно удаленная точка прямых, перпендикулярных диаметру
и
нам нужно доказать, что прямая
содержит эту точку, т. е. тоже перпендикулярна
Так как
то
Но
и
как касательные, проведенные из одной точки, следовательно,
т. е.
Ошибка.
Попробуйте повторить позже
(a) Даны окружность и точка внутри(вне) ее. Через точку
проведены четыре хорды
Пусть
– точка пересечения
прямых
и
— точка пересечения прямых
и
Докажите, что точки
лежат на одной
прямой.
(b) Докажите, что если четырехугольник вписан и описан, то прямая, соединяющая центры вписанной и описанной окружностей, проходит через точку пересечения диагоналей четырехугольника.
(a) Проективным преобразованием переведем точку в центр окружности, тогда точки
и
симметричны относительно центра
окружности при всех
Таким, образом при симметрии относительно
прямая
в
в
следовательно, точка
переходит в точку
что влечет коллинеарность точек
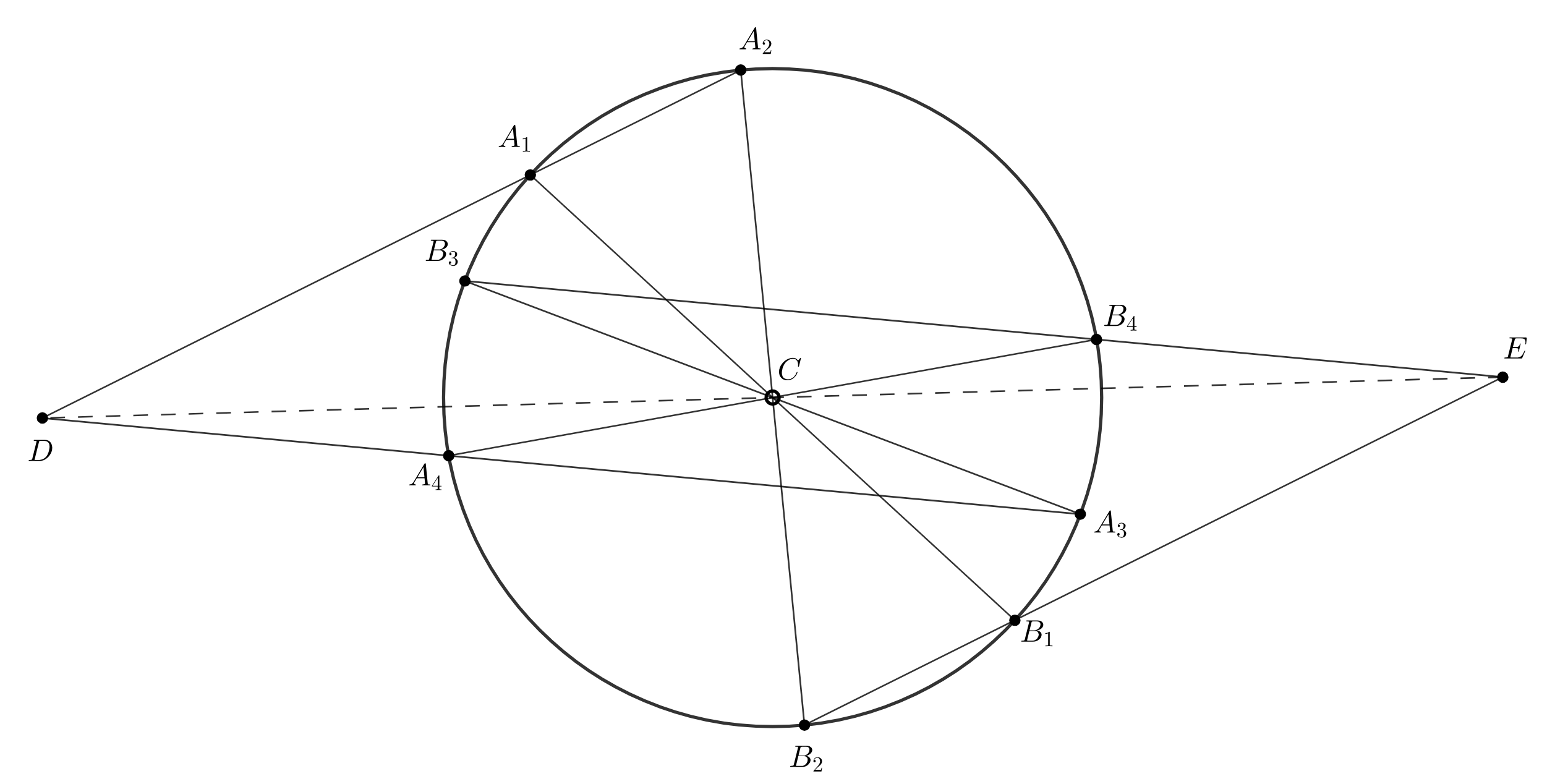
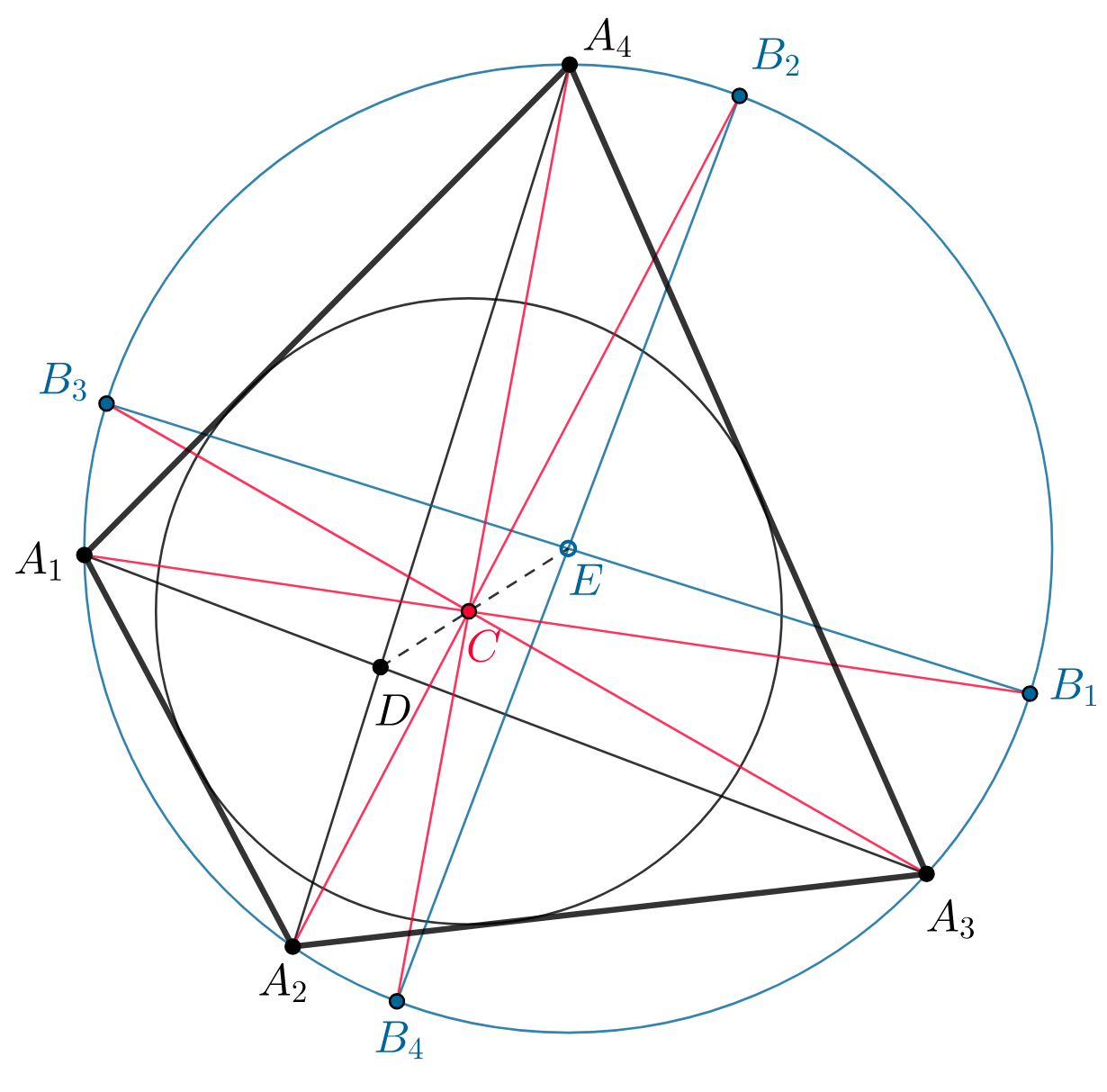
(b) Пусть — данный четырехугольник,
биссектрисы его углов. Так как в четырехугольник можно вписать
окружность, биссектрисы пересекаются в центре этой окружности — точке
Далее, точки
являются серединами двух
дополнительных дуг
описанной окружности, следовательно,
— диаметр этой окружности. Аналогично
— также
диаметр, и, значит, точка
— центр описанной окружности. Из пункта
следует, что прямая
проходит через точку
пересечения
диагоналей четырехугольника.
Ошибка.
Попробуйте повторить позже
Пусть — описанная окружность прямоугольного треугольника
(
) с центром в точке
Точка
— произвольная
точка на касательной к
в точке
— вторая точка пересечения
и
Точка
на
такова, что
Докажите, что
коллинеарны.
Рассмотрим проективное преобразование, которое переводит окружность в окружность, а точку в бесконечно удаленную. После
преобразования
т.е.
а значит
является серединным перпендикуляром к
следовательно,
Пусть
прямая
пересекает
в точке
тогда четырехугольник
является прямоугольников, тем самым
тогда
и четырехугольник
является трапецией. Наконец, точка
лежит на серединном перпендикуляре к
следовательно,
что влечет требуемое.

Ошибка.
Попробуйте повторить позже
Пусть — точки касания вписанной окружности
треугольника
со сторонами
соответственно.
Точки
и
на сторонах
и
соответственно таковы, что
и
является касательной к
Пусть
— середина отрезка
— точка пересечения прямых
и
Докажите, что
касается окружности
![]()
Пусть — прямая, параллельная
проходящая через
Поскольку
точка пересечения
прямых
и
лежит на
прямой
Рассмотрим проективное преобразование, переводящее вписанную окружность в окружность, а прямую
в
бесконечно удаленную, в частности, точка
переходит в бесконечно удаленную точку, тем самым, образы прямых
и
параллельны и
переходит в середину
поскольку двойное отношение
не изменится при
проективном преобразовании. Точка
так же переходит в бесконечно удаленную, а значит прямые
и
так
же параллельны, следовательно,
является ромбом, описанным около вписанной в
окружности,
— ее
диаметром.
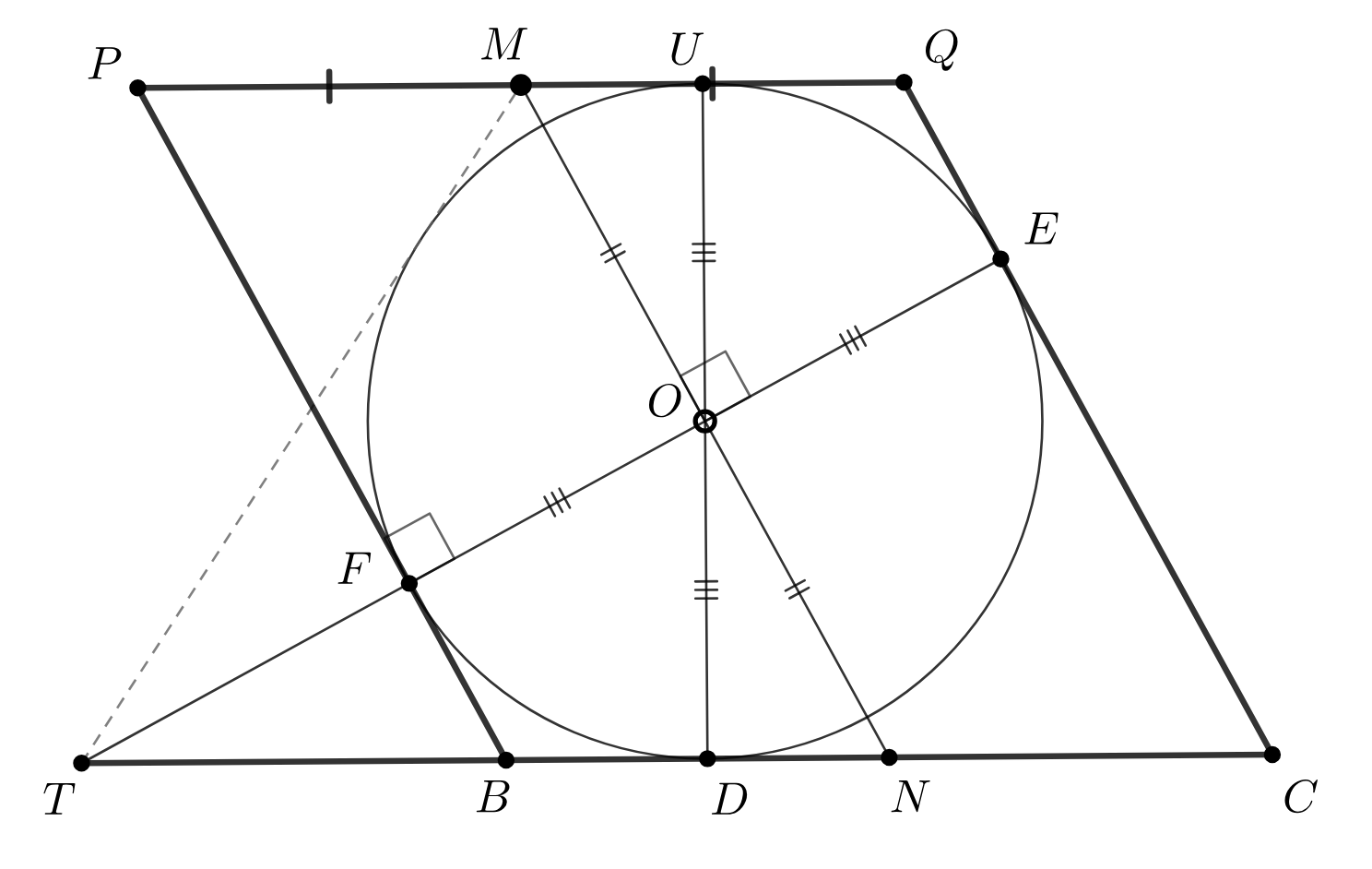
Пусть — центр вписанной окружности,
— точка касания окружности и прямой
— середина
Прямая
является
средней линией трапеции
следовательно
аналогично
следовательно,
лежат на одной прямой,
а в силу симметрии относительно
верно, что
. Наконец, под действием симметрии относительно
точки
и
переходят в друг друга, а значит прямые
и
переходят в друг друга, окружность переходит в себя, а значит
касается так же
касается окружности.
Ошибка.
Попробуйте повторить позже
Будем называть треугольник вписанным в треугольник
, если точки
,
,
находятся на сторонах
,
,
соответственно.
1. Докажите, что если отрезок параллелен отрезку
, то описанные окружности треугольников
и
пересекаются на
прямой
.
2. Оказалось, что ,
. Докажите, что точка, симметричная
относительно
, лежит на пересечении описанных
окружностей треугольников
и
.
3. Пусть . Средняя линия треугольника
, параллельная
, пересекает
и
в точках
и
соответственно. Докажите, что точка
,
,
,
лежат на одной окружности.
4. В треугольник вписан треугольник
, гомотетичный треугольнику
. Докажите, что описанная окружность
треугольника
касается описанной окружности
тогда и только тогда, когда касается описанной окружности
.
1. Пусть — вторая точка пересечения описанных окружностей
и
. Поскольку четырехугольник
описанный, то
. Четырехугольник
также описанный, значит
.
![]()
Поскольку , то
.
Получаем, что . Тогда
,
,
лежат на одной прямой.
2. Поскольку треугольники и
равнобедренные, то
и
. Тогда
Также из определения (точка, симметричная
относительно
) следует, что
Получается, что лежит на описанной окружности
.
![]()
Из определения как симметричной точки:
Значит, и
лежат на одной окружности с центром в
а
и
с центром в
Тогда выполнены следующие равенства
для вписанных и центральных углов:
Получаем, что лежит и на описанной окружности
.
3. Обозначим за и
середины
и
соответственно. Т.к.
, то
и
— касательные к
окружности, описанной около
.
![]()
Рассмотрим пару окружностей: описанная окружность треугольника и окружность нулевого радиуса с центром в точке
.
Рассмотрим степени точек
и
относительно данных окружностей:
Получаем, что — радикальная ось наших 2 окружностей. Тогда на этой же радикальной оси лежат
и
. Тогда
и
Следовательно,
— касательная к описанной окружности
, и
— касательная к
описанной окружности
. Тогда
4. Окружность повторно пересекает стороны
,
,
в точках
,
,
соответственно. Окружность
повторно пересекает стороны
,
,
в точках
,
,
соответственно.
Окружности и
повторно пересекаются в точке
. Заметим, что
поэтому лежит на окружности
. Также
поэтому лежит на окружности
. Аналогично
лежит на окружностях
,
.
Пусть — инверсия с центром в точке
и произвольным радиусом. Тогда
Также
Аналогично . Следовательно, треугольники
и
подобны. Проделывая аналогичные
рассуждения для двух других сторон мы получаем
Следовательно, угол между окружностями и
равен углу между окружностями
и
по подобию, с другой стороны, равен углу между окружностями
и
, поскольку инверсия сохраняет
углы.
Ошибка.
Попробуйте повторить позже
Даны две окружности и
, пересекающиеся в (несовпадающих) точках
. К этим окружностям проведены общие внешние
касательные, пересекающиеся в точке
. Прямая
повторно пересекает
в точке
, а прямая
повторно пересекает
в
точке
. Касательная к
в точке
и касательная к
в точке
пересекаются в точке
. Докажите, что точки
лежат на одной окружности.
Источники:
Назовём центры окружностей соответственно
и
Вторую точку пересечения
с
назовём
. Без ограничения
общности скажем, что радиус
меньше радиуса
(случай равенства радиусов невозможен, ведь тогда касательные не имели бы точки
пересечения). Тогда
лежит на отрезке
.
![]()
Докажем, что прямая составляет равные углы с касательной к
в точке
и с касательной к
в точке
. Гомотетия с
центром
и коэффициентом
переводит
в
, при этом точки пересечения прямой
с окружностью
переходят в
точки пересечения
с
в порядке их следования на луче
Значит, точка
перейдет в точку
, а точка
– в точку
При гомотетии касательная к в точке
переходит в касательную к
в точке
Согласно теореме о б угле между касательной
и хордой, касательные к
в точках
и
составляют равные углы с хордой
из чего следует, что прямая
составляет
равные углы с касательной к
в точке
и с касательной к
в
Утверждение доказано. (Отметим, что если касательные из
доказанного утверждения параллельны, то прямая
содержит
и
а значит точки
и
совпадают, что противоречит
условию.)
Осталось доказать Для этого рассмотрим прямую
являющуюся осью симметрии окружностей
и
относительно неё симметричны прямые
и
касательные к
в
и
Значит,
равен углу между
и
касательной к
в
этот угол равен
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике углы
и
— тупые. На сторонах
,
,
и
отмечены точки
,
,
и
соответственно. Докажите, что периметр четырёхугольника
больше удвоенной длины диагонали
.
Начертим четырёхугольник симметричный четырёхугольнику
относительно точки
и отметим соответствующие
точки
и
Заметим, что
так как
— тупой по условию, а
- середина отрезка
то есть
находится в той же полуплоскости относительно серединного перпендикуляра к
что и точка
Также заметим, что так как
симметричен
относительно точки
то
Далее продлим
на свою длину — точка
Отметим
на
точку
так, что
![]()
Аналогично отрезкам можем получить, что
(так как
- тупой по условию). Так
как
и
(
— параллелограмм). Таким образом, для пятиугольника
можем выписать неравенство:
Так как получаем, что:
Значит,



