Планарные графы
Ошибка.
Попробуйте повторить позже
Внутри квадрата отметили точек так, что никакие три из
точек (отмеченных и вершин квадрата) не лежат на одной прямой. Затем
некоторые точки соединили отрезками так, что квадрат разбился на треугольники. Какое количество треугольников при этом могло
получиться?
Подсказка 1
Для начала представим все отмеченные точки и вершины квадрата, как вершины графа, а отрезки и стороны квадрата будем считать ребрами. Тогда у нас есть планарный граф. Попробуйте вывести какое-нибудь соотношение на грани и ребра, учитывая что у нас все грани, кроме внешней являются треугольниками, а внешняя грань содержит только 4 ребра.
Подсказка 2
Выходит, что каждое ребро участвует в двух гранях, а, значит, верно: 3(F - 1) + 4 = 2E. Количество вершин в этом графе нам известно из условия, поэтому попробуйте воспользоваться формулой Эйлера, и найти F.
Будем считать отмеченные точки и вершины квадрата вершинами, а соединяющие их отрезки и стороны квадрата — рёбрами планарного
графа. Для каждого куска, на которые этот граф разбивает плоскость, подсчитаем число ограничивающих его рёбер, и все полученные
числа сложим. Поскольку каждое ребро разделяет два куска, то в итоге получим удвоенное число рёбер. Так как все куски, кроме внешнего
— треугольники, а внешний кусок ограничен четырьмя рёбрами, то верно: Заметим, что
Поэтому по формуле
Эйлера получаем, что:
Решаем это уравнение и получаем Так как есть еще внешняя грань, то треугольников
Ошибка.
Попробуйте повторить позже
Докажите, что в любом планарном графе найдется вершина степени или меньше.
Подсказка 1
Попробуйте предположить противное и оценить сумму степеней всех вершин снизу.
Подсказка 2
Также вспомните, что сумма степеней вершин = 2E.
Подсказка 3
Примените неравенство 3V - 6 ≥ E.
Пусть не так. Тогда каждая вершина графа имеет степень хотя бы А, значит, сумма степеней всех вершин хотя бы
Следовательно, получаем неравенство
а из него
А это в свою очередь противоречит неравенству
Ошибка.
Попробуйте повторить позже
Для двудольного графа неравенства и
можно усилить. Сделайте это, пожалуйста.
Подсказка 1
Что можно сказать про минимальную длину цикла в двудольном графе?
Подсказка 2
Правильно! Она хотя бы 4 в силу того, что все циклы в двудольном графе четной длины. Попробуйте написать неравенство, которое свяжет E и F, учитывая, что каждое ребро соответствует не более чем двум граням, а каждая грань состоит хотя бы из 4 ребер.
Подсказка 3
Получается, что верно неравенство 2E ≥ 4V. Попробуйте подставить его в формулу Эйлера.
В двудольном графе все циклы четной длины, поэтому в каждом цикле хотя бы ребра. А, значит, и в каждой гране хотя бы
ребра.
Следовательно, каждой гране соответствует хотя бы
ребра, а каждому ребру не более двух граней, то есть верно следующее неравенство:
Теперь подставим в формулу Эйлера. Получим, что
А, значит,
Замечание. На самом деле верно более общее утверждение. Если каждый цикл графа имеет длину хотя бы То верны следующие
неравенства:
Ошибка.
Попробуйте повторить позже
Можно ли ребра полного графа на вершинах покрасить в два цвета так, чтобы ребра каждого цвета образовывали планарный
граф?
Подсказка 1
Попробуем доказать, что это невозможно и пойдем от противного. Какие оценки на число ребер планарного графа мы знаем?
Подсказка 2
Верно! Их не более, чем 3В - 6. Как тогда сверху можно оценить число ребер в графе на одном цвете?
Подсказка 3
Верно, этих ребер не более 27 в каждом графе в отдельности, а в сумме точно не более 54. А сколько ребер всего в нашем графе?
Предположим, что раскрасить можно, тогда из неравенства для планарного графа , где
рёбра и вершины соответственно,
следует, что в каждом из графов на рёбрах первого и второго цветов не более
рёбер, то есть всего рёбер в графе не более
Но наш граф полный и в нём
вершин, а значит ребёр —
Противоречие.
Нельзя
Ошибка.
Попробуйте повторить позже
На плоскости отметили точек так, что никакие три не лежат на одной прямой. Затем все пары точек соединили отрезками. Какое
наименьшее количество точек пересечения этих отрезков могло получиться? Концы отрезков при этом не учитываются.
Подсказка 1
Пусть в графе есть некоторые точки пересечения. Какое наименьшее число ребер нужно удалить, чтобы он стал планарным?
Подсказка 2
Мы знаем для планарных графов неравенство Р ≤ 3В - 6. Какая оценка получается на максимальное число ребер в планарном графе?
Подсказка 3
Верно, ребер не более 12, а изначально их 15. Значит, удалить надо хотя бы 3, причем каждое удаление должно уменьшать число точек пересечения хотя бы на 1. Найдется ли подходящий пример?
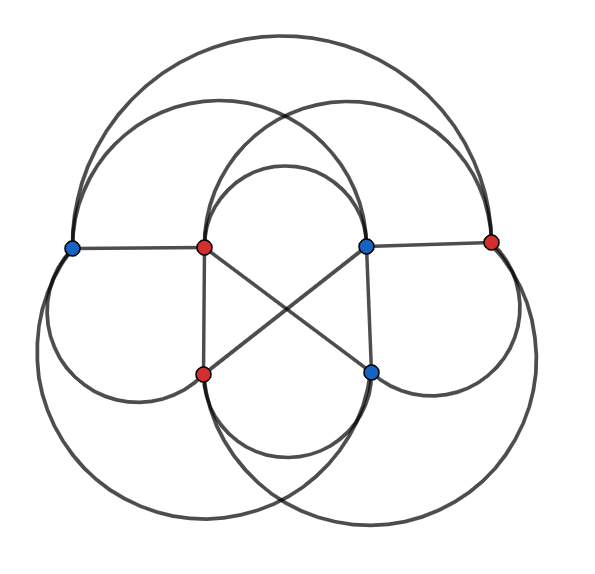
Попытаемся удалить из данного наименьшее количество рёбер так, чтобы он стал планарным. Из неравенства понимаем, что в
нём после удаления должно быть не более
рёбер, а изначально в нём
рёбер, значит необходимо удалить хотя бы
ребра. С
удалением каждого ребра исчезает хотя бы одно пересечение (иначе зачем удалять это ребро?). Таким образом, в исходном графе было хотя
бы
точки пересечения. Предъявим пример:
Ошибка.
Попробуйте повторить позже
Набор домино выложили на клетчатую плоскость так, чтобы доминошка занимала две клеточки. Цифру назовем обворожительной, если множество клеток, на которых она написана, связно по стороне. Какое максимальное количество обворожительных цифр может быть?
Пример (тут присутствуют не все доминошки, но те, которых нет, можно разместить произвольно):
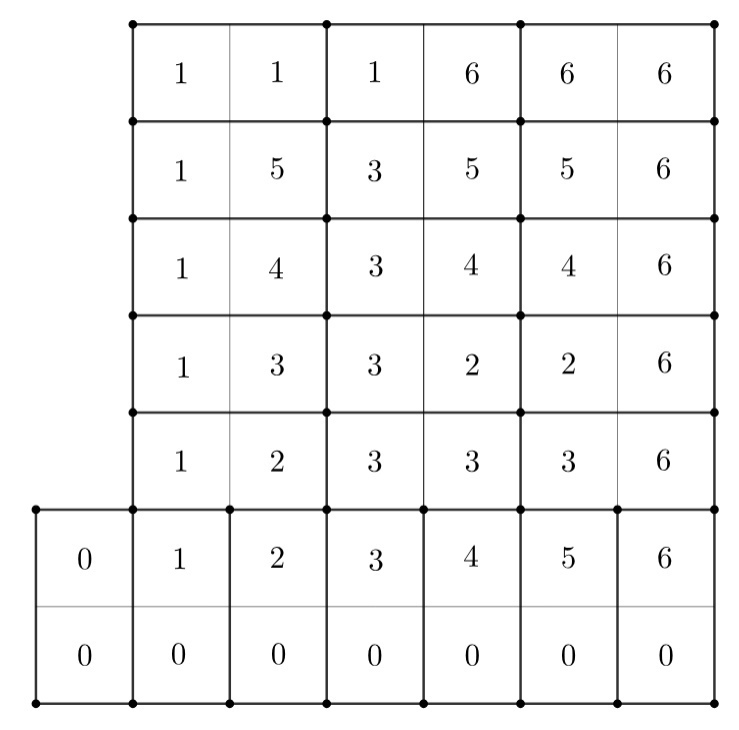
Оценка: Предположим, что имеется хотя бы обворожительных цифр. Введём граф следующим образом: пусть клетки — это вершины,
ребром соединим две вершины, если у соответствующих клеток есть общая сторона. Тогда нетрудно понять, что граф на вершинах, в
которых находятся обворожительные цифры, является связным и планарным. При этом, компонента с одной обворожительной цифрой
обязательно соединена ребром с компонентой с другой обворожительной цифрой, поскольку для любых двух цифр существует доминошка,
на которой есть эти цифры. Но тогда на этих пяти компонентах с обворожительными цифрами образуется полный граф на
вершинах, а
он планарным не является, противоречие.


