Экстремальные задачи в планиметрии
Ошибка.
Попробуйте повторить позже
В круговой сектор радиуса с центральным углом
вписаны две окружности (обе касаются радиусов-сторон сектора,
друг друга внешним образом, а большая касается окружности сектора). Какую наибольшую долю может составлять расстояние между
центрами вписанных окружностей от величины
и при каком значении
это достигается?
Источники:
Подсказка 1
Попробуем ввести обозначения, переписать данное через эти переменные и выразить искомое через них. Что лучше взять за x и y?
Подсказка 2
Пусть радиусы окружностей будут x и y. Мы можем записать следствие из подобия прямоугольных треугольников с катетами - радиусами окружностей. Как можно выразить (x + y) / R?
Подсказка 3
Пусть t = y / R. Тогда искомое можно выразить через t. Это будет парабола, наибольшее значение которой на отрезке можно найти через вершину.
Обозначим радиусы малой и большой вписанных окружностей через и
, введём величину
. Отметим, что
.
![]()
Выразим стороны треугольника через радиусы трёх окружностей.
Из подобия прямоугольных треугольников получаем
Откуда
Расстояние между центрами вписанных окружностей равно
.
Рассмотрим искомое отношение
Относительно величины это отношение есть парабола
. Выразим параметр
через угол
.
Таким образом, при изменении от
до
параметр
растёт от
до
. Остаётся найти максимум параболы
на
полученном отрезке
. Вершина параболы лежит правее отрезка, следовательно искомый максимум достигается при
и равен
.
при
Ошибка.
Попробуйте повторить позже
Четыре компьютера, расположенные в вершинах квадрата , соединены прямолинейными отрезками проводов с сервером, который
находится в точке пересечения диагоналей
. Сторона квадрата равна 2 м. Несложно заметить, что для такого подключения потребуется
метров провода. Чтобы уменьшить длину проводов, вам разрешается передвинуть сервер из точки
в любую другую
точку
, а также компьютер из точки
в любую другую точку
так, чтобы новая суммарная длина проводов
была как можно меньше. Разрешается компьютеры и сервер размещать в одной точке (например, точка
может совпасть с точкой
). Компьютеры в вершинах
двигать нельзя. Чему равно минимальное значение
?
Источники:
Подсказка 1
Что можно сказать о А₁ и O₁? Они совпадают, если мы ищем минимальное значение S(почему?). Тогда пусть А₁ = O₁ = K. Что можно сказать о расположении K? Где она должна лежать?
Подсказка 2
Симметричность расположения точек B и D, подсказывает, что сумма DK + KB наименьшая, когда K лежит на диагонали AC. Предположим обратное. Тогда нам нужна какая-то точка на диагонали, чтобы показать, что для неё S меньше. Какую бы выбрать?
Подсказка 3
Конечно, основание перпендикуляра K на AC, пусть это точка K₁. Если CK > CK₁ (длина наклонной и проекции), то что делать с DK + KB непонятно. Обычно на помощь всегда приходит неравенство треугольника. Но треугольника с необходимыми сторонами нет, значит, его нужно построить!
Подсказка 4
Теперь, когда доказано, что K лежит на диагонали, достаточно обозначит один из отрезков ОK или KC за x. Тогда S превратиться в некоторую функцию от х, у которой нужно будет найти минимум на отрезке [0; √2].
Заметим, что точки и
совпадают.
Действительно, пусть минимум достигается на конфигурации, где это не так. Но тогда, сдвинув точку в точку
, мы длину проводов уменьшим. Таким образом, компьютер
и сервер
должны оказаться в некоторой точке
Покажем, что лежит на диагонали
.
Предположим обратное. Пусть — основание перпендикуляра, опущенного из точки
на прямую
. Покажем, что сумма
расстояний от точки
до вершин
, которую обозначим
, меньше аналогичной суммы
. Длина проекции меньше длины наклонной, поэтому
. Чтобы доказать, что
отразим отрезок относительно прямой
(при этом точка
перейдет в точку
, точка
— в точку
).
![]()
Точки окажутся на одной прямой. Тогда
, и при этом
.
Неравенство (1) доказано. Следовательно,
, а значит, искомая точка
должна лежать на диагонали.
Пусть . Рассмотрим функцию
![]()
На отрезке функция
принимает минимальное значение в точке
а само минимальное значение
равно
Ошибка.
Попробуйте повторить позже
Дана трапеция с основаниями
и боковыми сторонами
. Точка
на прямой
такова, что
периметр треугольника
наименьший из возможных. Найдите этот периметр.
Источники:
Подсказка 1
Заметим, что основание у нашего треугольника зафиксировано. То есть на самом деле нам нужно найти минимальную сумму расстояний до точки P от A и B. Давайте попробуем понять, почему расстояние будет минимальным, когда лучи PA и PB будут падать под одним углом на BC. Обычно когда речь идёт о минимуме или максимуме, то нужно неравенство, а в геометрии чаще всего — это неравенство треугольника. Как можно попробовать сделать из отрезков PA и PB треугольник, в котором мы явно будем видеть их сумму?
Подсказка 2
Верно, хоть до этого и не просто догадаться, давайте попробуем отразить точку D симметрично относительно BC. Что тогда у нас получается? Пусть симметричная точка X. Получается треугольник APX, где сумма наших расстояний это AP+PX. Но тогда записав неравенство треугольника, когда достигается минимум?
Подсказка 3
Да, получается, чтобы сумма расстояний выстроилась в одну прямую, а это и будет минимум по неравенству треугольника, нужно как раз равенство углов. Победа! Теперь осталась только техническая часть поиска двух сторон равнобедренного треугольника APD. Это можно сделать, например, через теорему Пифагора для половины основания, высоты и стороны треугольника. Нужно только найти высоту трапеции, что при наличии стольких данных несложно.
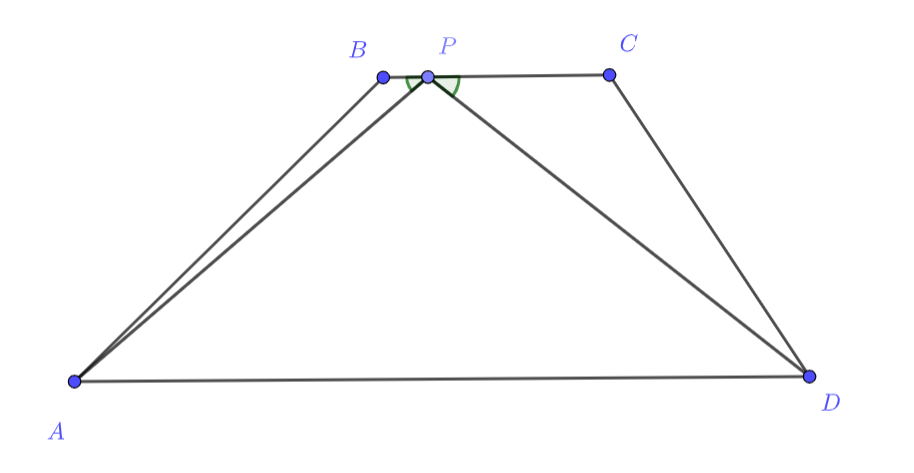
Первое решение.
Воспользуемся следующим утверждением, которое наиболее известно как «принцип наименьшего времени Ферма» в физике:
Для данных точек и данной прямой
из всех точек
сумма
будет минимальной, когда углы между прямыми
и
и
и
будут равны.
Тогда для искомой точки на прямой
должно выполняться равенство
(точки
и
- где-то «далеко» на
прямой
. Поскольку
, то
т.е. треугольник - равнобедренный. Значит, нам достаточно найти периметр равнобедренного треугольника
, где
- точка
на прямой
.
По теореме Пифагора этот периметр равен
где - расстояние между прямыми
и
, т.е. высота трапеции.
Найти высоту трапеции можно разными способами. Например, проведём через точку , прямую, параллельную
, до пересечения с
основанием
в точке
. Тогда искомая высота - это высота из вершины
в треугольнике
. Поскольку
параллелограмм, то
,
.
Итого, нам достаточно найти длину высоты на сторону длины 7 в треугольнике со сторонами 5 , . По формуле площади и
формуле Герона имеем
откуда
и окончательный ответ .
Второе решение.
Также, как и в первом решении, найдём высоту трапеции. Покажем здесь, как можно это было сделать по-другому. Опустим высоты
и
трапеции. Обозначим их длины через
, длину отрезка
обозначим через
. Поскольку
, для
получим
. Из прямоугольных треугольников
и
по теореме Пифагора получим
и
Подставив в эти равенства известные длины, получим систему уравнений
Вычитая из первого равенства второе, получим , откуда
. Тогда
.
Рассмотрим треугольник . Обозначим
, тогда
(здесь и далее все расстояния со знаком, т.е. могут быть
отрицательные). Опустим высоту
. Тогда треугольник
прямоугольный и по теореме Пифагора
Аналогично, из прямоугольного треугольника
Тогда периметр треугольника равен
Найдём производную этой функции:
Из уравнения получаем
откуда . Несложно видеть, что
именно точка минимума, откуда минимальный периметр равен
.
Ошибка.
Попробуйте повторить позже
Две стороны выпуклого четырёхугольника имеют длину 6, ещё одна — длину 1, а его площадь — наибольшая возможная при таких условиях. Какова длина четвёртой стороны четырёхугольника?
Источники:
Подсказка 1
Пусть наши известные стороны это b, b и c, но мы не знаем, в каком порядке они расположены в четырехугольнике: как b, b, c или b, c, b? А вдруг это не важно?)
Подсказка 2
Пусть наш четырехугольник это ABCD, где AB = CD = b, BC = c. Тогда на самом деле площадь четырехугольника AB'CD, где AB' = c, B'C = CD = b будет такой же, потому что треугольник ACD не изменился, а ABC = AB'C, то есть площадь осталась такой же) Давайте теперь мыслить про первый вариант.
Подсказка 3
Можно ли отдельно максимизировать площадь, учитывая наши условия? Например, разбить четырехугольник на какие-то части, и меняя что либо, менять площадь?
Подсказка 4
Давайте отдельно максимизируем площадь ABC и ACD) Начнем с ABC. Мы знаем, что A находится на расстоянии b от точки B. Так давайте будет двигать A по окружности с центром в точке B и радиусом b! Сторона BC как раз не меняется в таком случае. В какой момент площадь ABC будет максимальна?
Подсказка 5
Тогда, когда AB станет перпендикулярна BC! Потому что площадь ABC = 1/2 ⋅ (высота к BC) ⋅ BC, и высота максимальна будет как раз в этом случае. Попробуйте сделать тоже самое с ACD) Какой четырехугольник в таком случае у нас выйдет?
Подсказка 6
Т.к. углы ABC и ADC станут по 90°, то ABCD - вписанный, да и еще у него AB = CD, то есть ABCD - равнобокая трапеция! Осталось посчитать сторону AD, зная все это)
Подсказка 7
Для удобства подсчета, стоит опустить высоты из B и C на AD и воспользоваться формулой высоты в прямоугольном треугольнике)
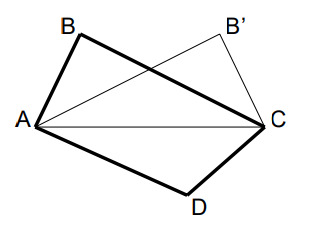
Пусть известные длины сторон четырехугольника равны и
В условии не указан порядок расположения этих сторон:
или
Но вместо четырехугольника
в котором, скажем
рассмотрим четырехугольник
в
котором,
В нем тот же набор известных длин сторон (но в другом порядке), а площади этих четырехугольников
равны, так как это суммы
и
причем
Поэтому можно считать, что
Заметим, что двигая точку по дуге окружности радиуса
с центром в точке
мы будем получать четырехугольник с тем же
набором известных длин сторон, с той же частью
а площадь части
будет наибольшей тогда, когда
(иначе при том
же основании
высота из точки
будет короче, чем
Двигая аналогично точку
вокруг точки
получим, что из свойства
максимальной площади четырехугольника
вытекает
Итак, имеются два прямоугольных треугольника и
с общей гипотенузой
и равными катетами
и
Значит,
треугольники равны, как и их высоты на гипотенузу, т.е.
— равнобедренная трапеция с тупыми углами
и
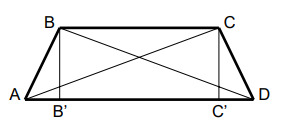
Пусть где
и
— проекции точек
и
на
Тогда из свойства высоты прямоугольного треугольника
получаем
Отсюда, с учётом того, что получаем
Подставляем и получаем
Ошибка.
Попробуйте повторить позже
Пусть радиусы описанной и вписанной окружностей треугольника равны
и
соответственно.
а) Прямая вторично пересекает описанную окружность треугольника
в точке
. Докажите, что
б) Докажите, что квадрат расстояния между центрами вписанной и описанной окружностей равен [Формула
Эйлера]
в) Докажите, что радиус описанной около треугольника окружности всегда не меньше, чем диаметр вписанной в данный треугольник окружности. А когда достигается равенство?
Пункт а), подсказка 1
Для начала можно применить лемму о трезубце и сказать, что WI = WB! А WB можно выразить с помощью теоремы синусов) Что теперь можно сделать с AI?
Пункт а), подсказка 2
Попробуйте опустить из точки I радиус на сторону AB, получится прямоугольный треугольник. А в нем AI выразить через угол и радиус вписанной окружности тоже можно, а дальше уже задача решается)
Пункт б), подсказка 1
Для начала перепишем формулу в виде R² - OI² = 2Rr. Если расписать разность квадратов, то получится произведение (R-OI)(R+OI)..Можно где-то найти такие отрезки?
Пункт б), подсказка 2
Да! Если провести диаметр через точки O и I! А дальше остается понять, почему произведение этих отрезков на этой прямой равно 2Rr. Для этого воспользуйтесь пунктом а)
Пункт в), подсказка 1
Просто смотрим на формулу из пункта б), и становится очевидно, что эта разность неотрицательная. А что делать с равенством?
Пункт в), подсказка 2
Из той же формулы получаем, что при равенстве OI = 0, т.е. I = O. А когда такое может быть?)
Решение пункта (а)
![]()
Пусть Из условия следует, что
— биссектриса угла
, то есть
Поэтому . По лемме о трезубце
Пусть — проекция точки
на
. Из прямоугольного треугольника
находим, что
Итого
Решение пункта (б)
![]()
Переписав формулу в виде , докажем, что обе ее части равны произведению
, где
— точка пересечения
биссектрисы угла
с описанной окружностью.
Пусть — точки пересечения прямой, содержащей
и окружности, описанной около треугольника
По свойству пересекающихся хорд
И по доказанному ранее в пункте (а) , поэтому
Первый вариант решения пункта (в)
По формуле Эйлера
Так как правая часть неотрицательна, то и левая часть неотрицательна, то есть
Получаем, что , то есть радиус описанной окружности всегда не меньше диаметра вписанной окружности.
Равенство достигается тогда и только тогда, когда
То есть центр вписанной окружности совпадает с центром описанной окружности. Это означает, что биссектрисы являются серединными перпендикулярами. Так как это выполняется для любой вершины треугольника, то каждая пара сторон треугольника является парой равных сторон. То есть треугольник является равносторонним.
Второй вариант решения пункта (в)
![]()
Пусть и
— вписанная и описанная окружности треугольника
. Через каждую вершину этого треугольника проведём
прямые, параллельные противолежащим сторонам. Получим треугольник
, подобный данному с коэффициентом
. Пусть
—
радиус вписанной окружности треугольника
.
Опишем около окружности треугольник
, стороны которого соответственно параллельны сторонам треугольника
так, что прямая
и точка
расположены по разные стороны от прямой
, прямая
и точка
— по разные стороны от
прямой
, прямая
и точка
— по разные стороны от прямой
Треугольник подобен треугольнику
и, следовательно, треугольнику
. Стороны треугольника
не
меньше соответствующих сторон треугольника
(второй из этих треугольников целиком заключён внутри первого). Поэтому
Равенство достигается только в случае, когда все стороны треугольника касаются окружности
. Тогда
Следовательно, То же верно для остальных углов. Треугольник является правильным.
Третий вариант решения пункта (в)
Пусть и
— стороны треугольника,
— полупериметр,
— площадь. Тогда
Положим
Имеем
Где последнее — в силу неравенства о средних для трёх чисел.
Следовательно, . Равенство достигается, когда
, то есть
в случае равностороннего треугольника.
Ошибка.
Попробуйте повторить позже
Высота остроугольного треугольника
пересекается с его другими высотами в точке
Точка
лежит на отрезке
так,
что величина угла
максимальна. Найдите
если
Источники:
Подсказка 1
Чтобы найти наибольшую величину угла, попробуем искать наибольшее значение одной из тригонометрических функций этого угла. Какую будет использовать удобнее всего? В △BKH нет прямых углов, поэтому подумайте через какие углы лучше всего выразить ∠BKH?
Подсказка 2
tg(x-y) = (tg(x) - tg(y)) / 1 + tg(x) * tg(y). Заменив длину неизвестной стороны DK за x, получим функцию от x, максимум которой мы ищем
Подсказка 3
Производная функции обнуляется при x² = BD * BH. Как выразить это произведение через AD и DC?
Подсказка 4
tg(∠HAD) = ctg(∠BCD)
![]()
Чем больше острый угол, тем больше его тангенс. Поэтому условие максимальности угла можно заменить на условие
максимальности его тангенса. По формуле тангенса разности имеем
Максимум этого выражения достигается при том же значении , что и минимум выражения
где Производная
равна
и обращается в нуль при
(нас интересуют только положительные
значения
Заметим, что откуда
Таким образом,
Ошибка.
Попробуйте повторить позже
В выпуклом 12-угольнике все углы равны. Известно, что длины каких-то десяти его сторон равны 1, а длина ещё одной равна 2. Чему может быть равна площадь этого 12-угольника?
Источники:
Подсказка 1
Пусть длины сторон это 10 единиц, 2 и x. Очень хочется найти x... Попробуем рассмотреть векторы, соответствующие сторонам и поработать с ними.
Подсказка 2
Т.к. мы всё-таки хотим использовать длины сторон, то работать будем не с самими векторами, а с коллинеарными им единичными. Т.к. мы знаем, что они образуют многоугольник, то мы можем записать уравнение на них. А как быть с равными углами? Что можно сказать о взаимно расположении некоторых единичных векторов?
Подсказка 3
Заметим, что каждый угол равен 150. Тогда мы можем сказать, какие стороны многоугольника параллельны. Теперь мы можем записать условия на пары единичных векторов.
Подсказка 4
Знаем, что сумма единичных векторов, где один идёт с коэффициентов 2, а другой - с x равна 0. Также сумма единичных векторов, соответствующим противоположным сторонам тоже равна 0. Как найти x?
Подсказка 5
Чему равна сумма единичных векторов без дополнительных коэффициентов?
Подсказка 6
Их сумма равна 0! Теперь-то мы можем найти x) Осталось лишь найти площадь многоугольника, в котором мы знаем взаимное расположение всех сторон.
Рассмотрим 12-угольник удовлетворяющий условию задачи. У него десять сторон длины 1 и одна сторона длины 2.
Обозначим через
длину оставшейся стороны. Рассмотрим векторы
а также коллинеарные им единичные
векторы
Тогда для некоторых
и
имеет место равенство
Помимо того,
поэтому
Вычитая второе из полученных равенств из первого, получаем
Это возможно лишь в случае, если и
Значит, в исходном 12-угольнике есть пара параллельных сторон длины
2.
В силу равенства всех углов и соответствующих сторон этот 12-угольник имеет ось симметрии:
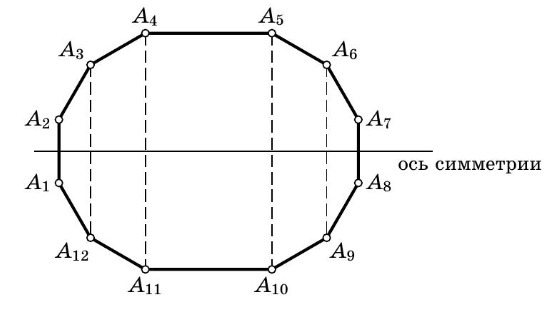
Чтобы найти площадь, разобьём его на 4 трапеции и прямоугольник. Находим
,
поэтому искомая площадь равна
Ошибка.
Попробуйте повторить позже
Назовём расположенный в пространстве треугольник удобным, если для любой точки
вне его плоскости из отрезков
и
можно сложить треугольник. Какие углы может иметь удобный треугольник?
Подсказка 1
Если поразмыслить над этой задачей, порисовать какие-то треугольники и точки Р, можно понять, что если брать точку Р очень близко к одной из вершин (допустим, к А), выполнение неравенства треугольника для РА, РВ, РС сводится к тому, что АВ и АС не могут быть сильно отличны по длине.
Подсказка 2
Конечно, мысли из первой подсказки нужно формализовать. Тогда мы придем к тому, что если условие задачи выполнено, то треугольник АВС равносторонний. Теперь для равностороннего треугольника нужно доказать, что для любой точки P условие задачи выполнено.
Подсказка 3
Доказывать это можно по-разному. Один из способов (красивый) — явно построить треугольник со сторонами, равными PA, PB и РС, используя подобия.
Докажем сначала, что неравносторонний треугольник под условие подходить не может. Предположим противное, пусть такой треугольник
есть и в нём
причём длины этих сторон различаются хотя бы на
Рассмотрим точку расположенную на перпендикуляре к плоскости
проходящем через точку
на расстоянии
от
Тогда
Можно выбрать настолько близко к вершине
уменьшая
чтобы
и
отличались соответственно от
и
меньше, чем на
и чтобы
было меньше
Тогда стороны
и
будут различаться более чем на
а длина стороны
меньше
— противоречие с неравенством треугольника.
Покажем теперь, что равносторонний треугольник удобен. Пусть Отметим на лучах
точки
так, чтобы выполнялись равенства:
Треугольники и
подобны по углу и отношению двух сторон, откуда
Аналогично вычисляем длины остальных сторон. Получаем, что треугольник — искомый.
Ошибка.
Попробуйте повторить позже
Из равнобедренного треугольника с углом при вершине и площадью 1 вырезают максимальный по площади круг, а из него —
максимальный по площади треугольник, подобный исходному. Какое наибольшее и наименьшее значение принимает площадь
полученного в итоге треугольника при
Источники:
Подсказка 1
Для начала поймём, что это за треугольники и окружности — очевидно, что это соотвественно вписанная окружность и вписанный в нее треугольник (иначе, мы могли бы увеличить площадь, дополнив до вписанной/ого). Значит, площадь вырезанного треугольника легко считается и выражается через наши параметры — площадь начального и угол. Однако нужно ли нам выражать? Просто ли так нам дали площадь большого?
Подсказка 2
Конечно, не просто так. Нам можно получить лишь отношение сторон и найти отношение площадей как коэффициент подобия в квадрате. Поэтому, найдя отношение сторон, мы сможем его промаксимизировать. Но через что выразить? Через стороны большого треугольника долго и некрасиво, а вот через радиус и угол - более чем! Подумайте лишь над тем, всегда ли одинаково все выражается.
Подсказка 3
При разных alpha размер стороны вырезанного треугольника выражается одинаково, вот только угол будет разный в зависимости от того, тупой ли треугольник, но синус остается неизменным. Осталось понять, как нам максимизировать функцию отношения… Но ведь она монотонна!
Пусть дан треугольник
— это середина
Заметим, что максимальный по площади круг лежащий в данном треугольник
является кругом, ограниченный вписанной окружностью. Пусть
— центр вписанной окружности,
и
— радиус окружности.
![]()
Тогда половина основания можно вычислить из подобия и
Так как вырезаемый треугольник подобный исходному
лежит внутри фиксированной окружности, то у него по
крайней мере две вершины лежат на окружности, в противном случаи мы сможем увеличить площадь. Дальше рассмотрим два варианта:
-
Исходный треугольник
остроугольный или прямоугольный, то есть тогда
Тогда треугольник
будет вписан в вырезанную окружность.
В этом случаи половина основания вырезанного треугольника равна
-
Исходный треугольник
тупоугольным, то есть тогда
Тогда треугольник
будет расположен так, что
будет диаметром вырезанной окружности.
В этом случаи половина основания вырезанного треугольника равна
В итоге получаем
Тогда коэффициент подобия будет равен
В силу подобия и
и того, что площадь исходного треугольника была равна 1, получаем, что
Функция убывает при то есть
поэтому
Ошибка.
Попробуйте повторить позже
На сторонах и
квадрата
соответственно отмечены точки
, отличные от вершин. Известно, что длина
стороны квадрата равна 1. Доказать, что выполнены неравенства:
Источники:
Подсказка 1
У нас есть картинка, где абсолютно случайно, независимо друг от друга, выбирается 4 точки на разных сторонах квадрата. Это значит как минимум то, что либо нам надо будет объединить все слагаемые в полученной сумме (пока непонятно какой, но точно выражающей сумму из условия) в одно слагаемое, которое зависит только от стороны квадрата, либо нам надо оценивать каждое слагаемое по отдельности. Выразите каждое слагаемое из условия и попробуйте применить рассуждения выше.
Подсказка 2
Верно, можно сгруппировать наши слагаемые по частям стороны. Тогда каждая пара слагаемых будет иметь вид x² + (1 - x)². Как тогда получить оценку на каждое слагаемое, а значит, по соображениям из первой подсказки, и на всю сумму?
![]()
По теореме Пифагора
Сложим эти равенства и перегруппируем результат в виде:
Каждое из выражений в скобках имеет вид для некоторого
и заключено в пределах от
включительно до
невключительно. Следовательно, сумма
заключена от
включительно до
невключительно.
Ошибка.
Попробуйте повторить позже
Бумажный квадрат площади 17 согнули по прямой, проходящей через его центр, после чего соприкасающиеся части склеили. Найдите максимально возможную площадь получившейся бумажной фигуры.
Источники:
Обозначим сторону квадрата через Пусть прямая отсекает от стороны квадрата
отрезок
Найдём
.
![]()
Обозначим . Поскольку из треугольника
(здесь
это проекция точки
на основание
)
находим
, то
Следовательно катеты прямоугольных треугольников равны и
. Откуда искомая площадь равна
С помощью производной можно получить, что максимум функции
достигается при , что соответствует углу
Ошибка.
Попробуйте повторить позже
Координаты вершин треугольника
являются решениями уравнения
Найти наименьшее возможное значение площади треугольника.
Уравнение равносильно системе
Решения расположены в узлах «косой» решетки на плоскости образованной семейством прямых
Если две вершины, например, и
, искомого треугольника
наименьшей площади лежат на прямых семейства
, то
и
являются соседними вершинами решетки (в противном, его площадь может быть уменьшена) и
Вершина находится на соседней (параллельной) прямой из семейства
(иначе площадь может быть уменьшена). Поскольку
расстояние между соседними прямыми из семейства
одинаковое и равно
, площадь треугольника
равна
.
Если две вершины, например,
и
, находятся на прямой семейства
и являются соседними узлами решетки,
то
Вершина находится на соседней (параллельной) прямой семейства
Поскольку расстояние между соседними прямыми из
семейства
одинаковое и равное
, площадь треугольника равна
Ошибка.
Попробуйте повторить позже
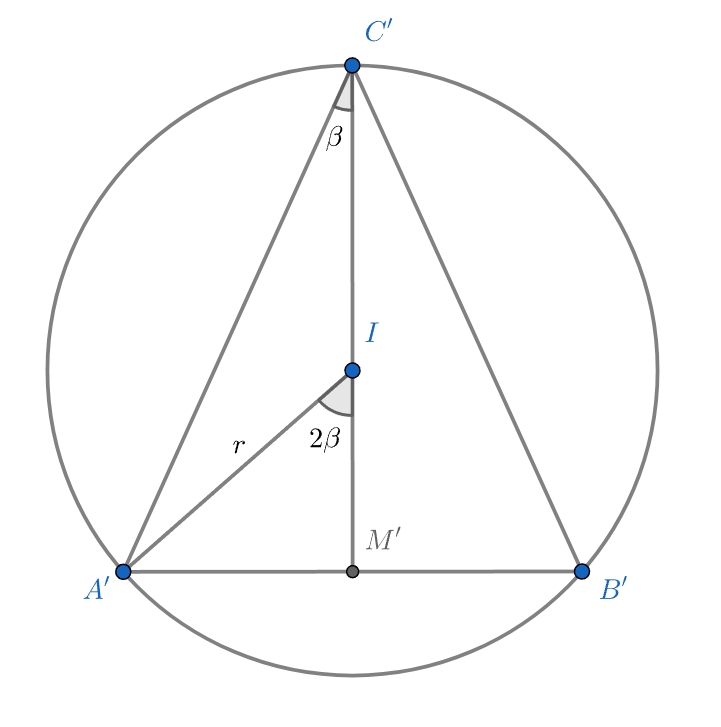
В треугольник , в котором сумма сторон
и
в
раз больше стороны
, вписана окружность, касающаяся сторон
и
в точках
и
соответственно. Отношение площади треугольника
к площади треугольника
равно
.
Найдите при данных условиях:
а) наименьшее значение ;
б) все возможные значения .
Источники:
Подсказка 1!
Для начала посмотрим на пункт а. Заметим, что у нас тут есть какие-то отрезки касательных, может быть мы можем выразить их через стороны треугольника как-то..?
Подсказка 2!
Верно! MC = NC = Полупериметр - c! А еще в треугольнике MNC две равных стороны, которые мы можем так выразить. Тааааааак, а как бы нам теперь зная много сторон найти отношение площадей?
Подсказка 3!
В таких случаях мы пишем отношение площадей через формулу двух сторон и угла между ними! Было бы здорово, если бы угол был общий, попробуйте угол С?
Подсказка 4!
А теперь в получившейся формуле осталось прийти к минимуму! (a+b) и ab, что-то знакомое..
Подсказка 5!
Хм, а пункт б? Раскроем скобки в последнем выражении для отношения площадей и сделаем замену t = a/b! Тогда что будет в скобках? В точности t+1/t+2. Осталось найти возможные значения t!
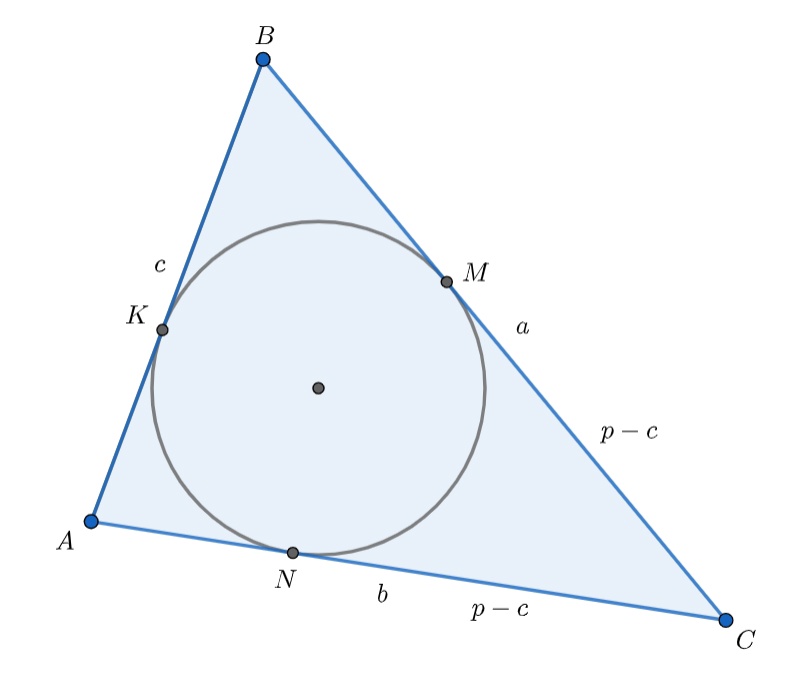
а) По формуле отрезков касательных для вписанной окружности имеем — стороны
треугольника, отсюда
Используем неравенство о средних (знак равно достигается, только в случае
), то
.
б) Перепишем отношение площадей в следующем виде:
где . По неравенству треугольника
. Учитывая то, что
последние неравенства
равносильны
. Отсюда
. Функция
монотонно убывает на
и возрастает на
, она
симметрична относительно
, откуда
. В итоге находим множество значений
на
отрезке
. Любое промежуточное значение можно задать выбором
и
.
а)
б)
Ошибка.
Попробуйте повторить позже
На листе бумаги нарисован прямой угол с вершиной Пятиклассник Петя хочет провести несколько лучей с той же вершиной, лежащих
внутри угла, так, чтобы сумма всех получившихся при этом углов составляла
градусов. Какое наименьшее число лучей он может
провести?
Источники:
Если он проведёт один луч, то сумма всех трёх получившихся углов составит градусов. Если лучей будет два, то получим три угла, при
суммировании которых каждый крайний угол будет учитываться три раза, а средний четыре раза. Тогда при суммировании всех углов мы
получим меньше
градусов. Если же провести три луча, то всего получится
углов, причём при их суммировании два крайних угла
учитываются по
раза, а два средних по
раз. Если сумма двух средних углов будет составлять
градусов, то вся сумма как раз даст
градусов. Так что три луча провести можно, и делать это нужно так, чтобы угол между двумя не соседними лучами составлял
градусов.
Три луча
Ошибка.
Попробуйте повторить позже
Четырёхугольник вписан в окружность. Пусть
– центр вписанной в треугольник
окружности. Найдите наименьшее
значение
, если известно, что
Источники:
Подсказка 1
Видим середину дуги и центр вписанной окружности, значит...
Подсказка 2
Они лежат на одной прямой, и можно применить лемму о трезубце!
Подсказка 3
Мы получили кучу отрезков, равных 2. Тогда хочется найти ещё побольше равных треугольников!
Подсказка 4
Давайте опустим перпендикуляры из точки I на AB и BD, и из точки C на BD. Мы получим три равных треугольника, и из этого будет следовать, что...
Подсказка 5
Эти перпендикуляры равны! Что тогда можно сказать про точку пересечения BD и CI?
Подсказка 6
Она делит CI пополам! Теперь осталось только применить теорему о произведении отрезков хорд и неравенство о средних, и мы найдём наименьшее значение BD. Ну и формально говоря, ещё нужно показать, как построить пример, когда это наименьшее значение достигается.
Из условия следует равенство дуг и
значит, биссектриса
угла
пересекает окружность в точке
. По лемме о
трезубце
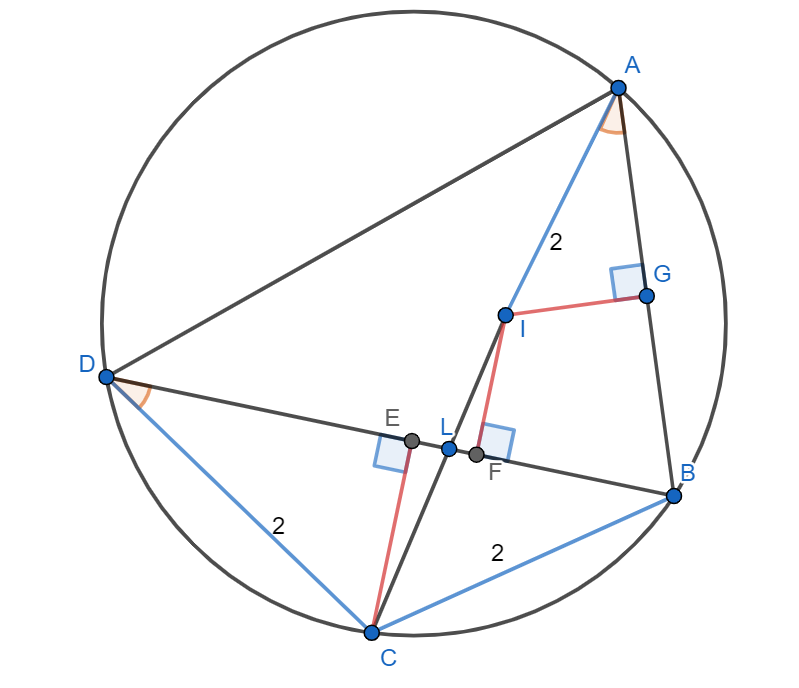
Пусть – основания перпендикуляров, опущенных из точек
и
на
и
соответственно, тогда из равенства
прямоугольных треугольников
и
по острому углу (равные вписанные углы) и гипотенузе (из условия) следует, что
Перпендикуляр
к диагонали
также равен
(это радиусы вписанной окружности треугольника
поэтому
пересекает отрезок
в его середине
из равенства прямоугольных треугольников
и
по катету и острому углу
(вертикальные).
Таким образом, По теореме о произведении отрезков хорд
Пусть
тогда
А
по неравенству о средних
Наименьшее значение достигается при Построим равнобедренный треугольник
с боковыми сторонами
и высотой
Тогда
Продлим
за точку
на длину
получим точку
Отметим
—
центр вписанной окружности треугольника
Тогда из леммы о трезубце получим
а значит,
и
построенная картинка удовлетворяет условию.
Ошибка.
Попробуйте повторить позже
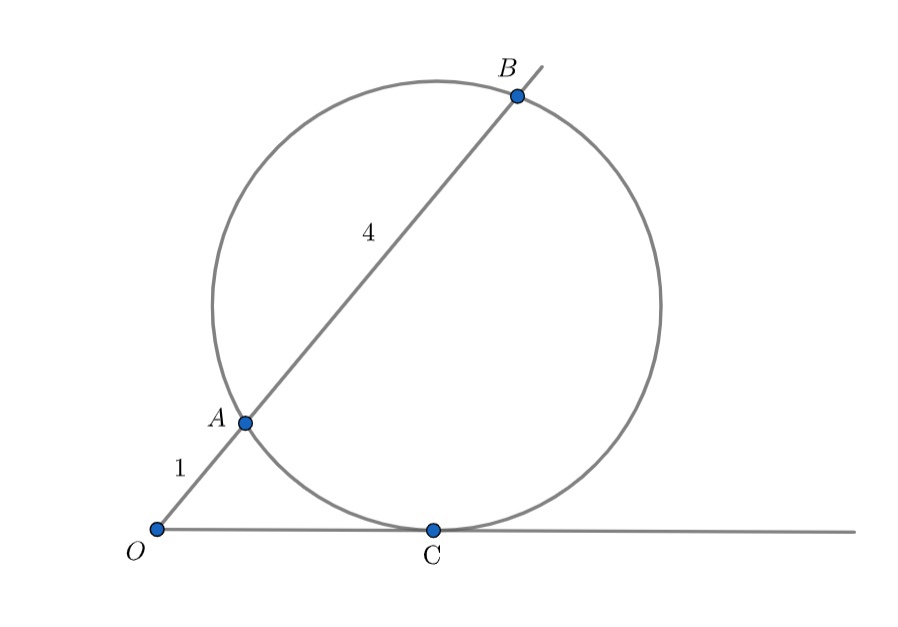
В окружность с центром вписан четырехугольник
, диагонали
и
которого пересекаются в точке
, причем
. Определите, какой может быть наименьшая длина диагонали
, если известно, что стороны
и
равноудалены от точки
.
Подсказка 1
Какой вывод можно сделать из равноудаленности AB и AD от точки O?
Из равноудалённости сторон и
от точки
вытекает их равенство. Следовательно равны углы
.
Таким образом, треугольники
и
подобны. Откуда
, т.e.
, а следовательно,
. Так как
, то
Следовательно,
применяя . Остаётся заметить, что данный случай реализуется, когда
проходит через центр окружности.
Ошибка.
Попробуйте повторить позже
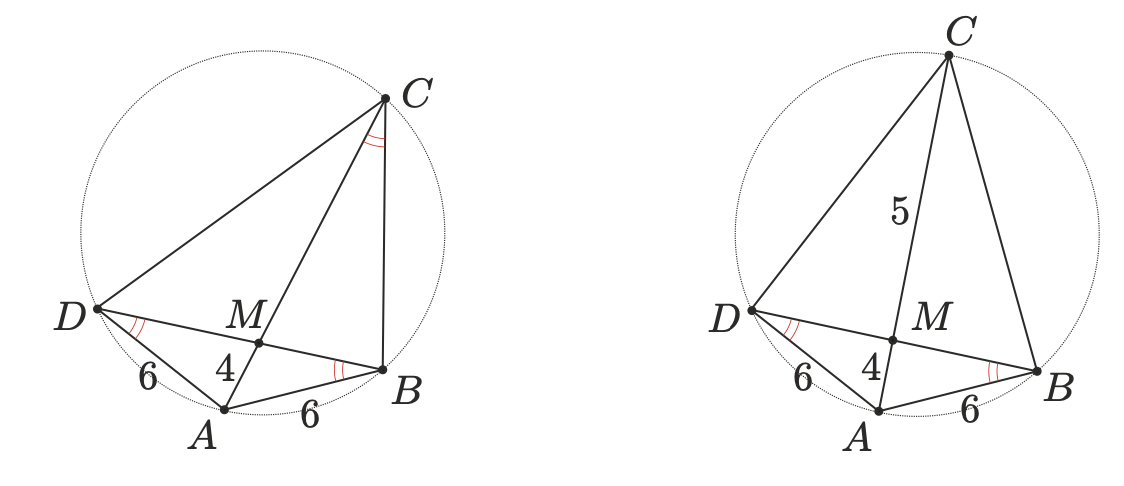
На одной из сторон острого угла с вершиной взяты точки
и
, а на другой – точка
. При какой длине отрезка
величина
угла
максимальна, если
Проведем через точки и
окружность, касающуюся второй стороны угла. Если
— точка касания, то угол
равен половине
дуги
В противном случае угол
равен полуразности дуги
и второй дуги, высекаемой углом
— т. е. будет меньше.
Остается воспользоваться тем, что квадрат касательной равен произведению секущей на ее внешнюю часть, откуда
.



