Сферы

Пусть — нижнее, а -— верхнее основание данной усечённой пирамиды; и — центры этих оснований (соответственно); и — середины рёбер и (соответственно). Из теоремы о равенстве отрезков касательных, проведённых к шару из одной точки, следует, что

и

следовательно,

Но , то есть

Поэтому данная в условии усечённая пирамида треугольная. Обозначим длину ребра нижнего основания через , верхнего — через . Так как шар касается всех рёбер пирамиды, её боковая грань — описанная равнобокая трапеция с основаниями и .

Радиус вписанной окружности найдем из прямоугольного треугольника :

, следовательно, . Но

поэтому

Имеем , откуда так как . Значит,

Из условия понятно, что — правильный тетраэдр. Попарные расстояния между точками обозначим через

Введем обозначения: — середины ребер и Пусть — длины отрезков и а длины отрезков соответственно равны и

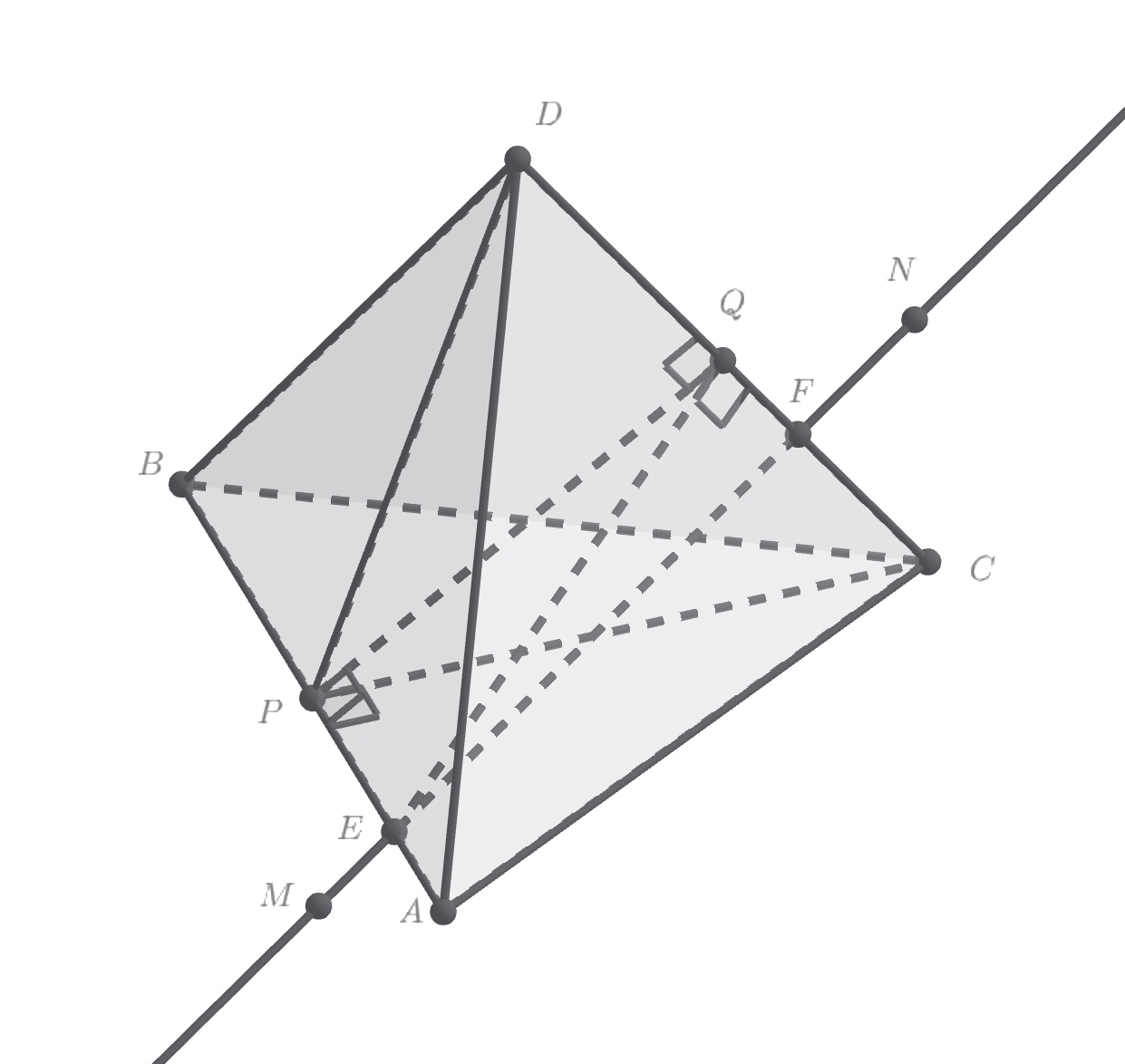
Треугольник — равнобедренный и — его медиана, перпендикулярная Тогда

Плоскость треугольника перпендикулярна поэтому и — пересекающиеся хорды сферы, поэтому

(1)

и – пересекающиеся хорды сферы, поэтому

(2)

Складывая и получим

(3)

Треугольники и прямоугольные (теорема о трёх перпендикулярах), поэтому

(4)

Используя то, что квадрат величины неотрицательное число и равенства и получаем:

Таким образом, должно выполняться что невозможно, так как

Значит, указанное отношение длин невозможно.

1. Нахождение высоты пирамиды

Пусть дана правильная треугольная пирамида с вершиной и центром основания Центр вписанной сферы лежит на её высоте Пусть — середина ребра основания Тогда — апофема пирамиды. Рассмотрим осевое сечение которое является равнобедренным треугольником. В этом сечении круг, являющийся сечением вписанной сферы, вписан в угол Этот угол образован апофемой пирамиды и радиусом вписанной в основание окружности

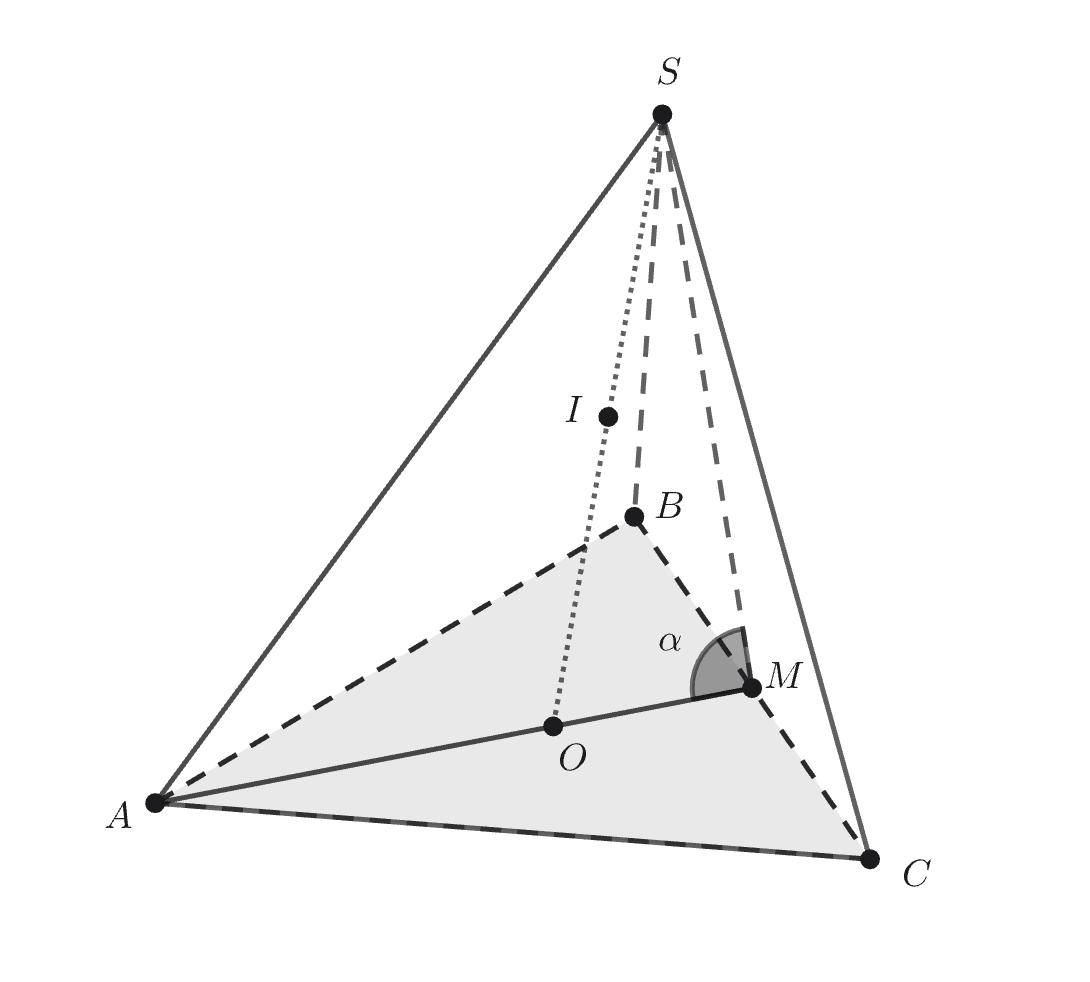
Пусть — радиус вписанной сферы, — радиус окружности, вписанной в основание пирамиды, и — двугранный угол при ребре основания. Они связаны соотношением

Подставим известные значения:

Отсюда находим :

Теперь найдем по формуле двойного угла:

Вычислим :

Подставим в формулу для :

Высота пирамиды связана с и углом через тот же треугольник в сечении:

2. Нахождение радиуса описанной сферы

Центр описанной сферы также лежит на высоте пирамиды. Радиус описанной сферы для правильной пирамиды можно найти по формуле

где — радиус окружности, описанной около основания.

Основание пирамиды — правильный треугольник. Для правильного треугольника радиус описанной окружности вдвое больше радиуса вписанной окружности :

Мы получили, что Это означает, что центр описанной сферы совпадает с центром основания пирамиды. В этом случае радиус описанной сферы равен радиусу окружности, описанной около основания.

Проверим это, подставив в общую формулу для :

Итак,

Пусть в основании пирамиды лежит 2024-угольник , точка — вершина пирамиды. Пусть для всех , сфера касается ребер в точке , а ребер в точке ().

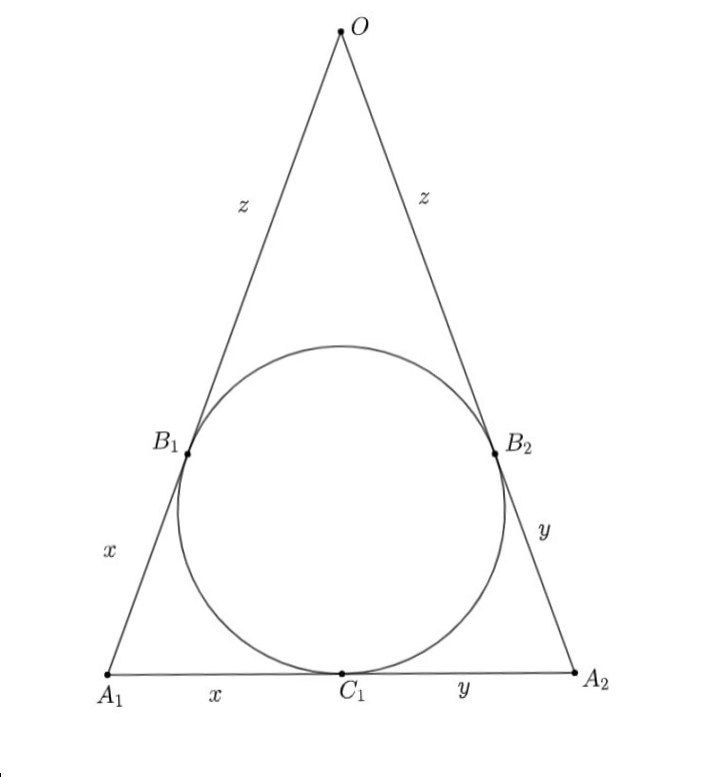
Рассмотрим треугольник . Сечением сферы в его плоскости является вписанная в него окружность, которая касается его сторон в точках , , . Пусть

Из теоремы косинусов имеем

Как известно,

По условию достаточно показать, что произведения квадратов половинных синих и половинных красных углов равны. Но из равенства выше каждое из таких произведений равно произведению отношений для всех , что доказывает исходное равенство.

Введём декартову систему координат с центром в точке , ось абсцисс — луч , ось ординат — луч , ось аппликат — луч .

Пусть — проекция центра сферы на грань куба. Определим ее местоположение. Так как сфера касается прямых и проходит через точку , то расстояние от точки до прямых и и точки одинаково (обозначим его ). Тогда лежит на луче , который является биссектрисой угла . Осталось учесть условие, что центр сферы касается прямой , то есть нужно проверить, что расстояние от центра до прямой совпадает с радиусом сферы .

Заметим, что есть два случая расположения точки (на рисунке показаны разными цветами):

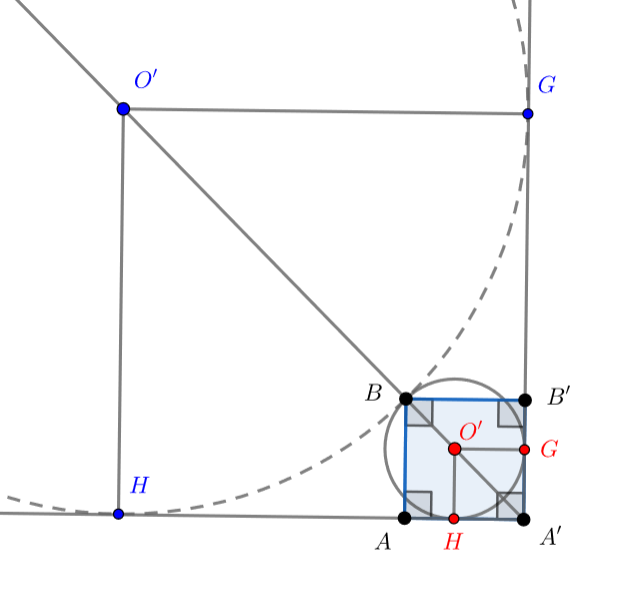
Случай 1: точка лежит на диагонали .

Тогда из теоремы Пифагора для прямоугольного треугольника получим: , откуда . Значит, центр сферы имеет координаты .

Расстояние до прямой равно . То есть радиус

Случай 2: точка лежит на продолжении луча .

Тогда из теоремы Пифагора для прямоугольного треугольника получим: , откуда . Значит, центр сферы в этом случае имеет координаты .

Расстояние до прямой равно . То есть радиус

Первое решение.

Сделаем гомотетию с центром и коэффициентом 2. Пусть — образы точек — точка пересечения прямой с плоскостью . Тогда как касательные к сфере, и, поскольку треугольники и подобны, то . Аналогично . Но как касательные, следовательно — центр окружности , а середина — центр окружности

______________________________________________________________________________________________________________________________________________________

Второе решение.

Обозначим сферу, проходящую через точки , с центром в точке , через , вписанную сферу пирамиды — через , а плоскость, проходящую через середины рёбер пирамиды — через .

Сделаем инверсию с центром в точке , переводящую в . Тогда точки перейдут в точки . Так как , то образ будет перпендикулярен . Следовательно, образом будет сфера, построенная на окружности ( ) как на диаметральной окружности.

Тогда утверждение задачи следует из того, что центр инверсии, центр сферы и центр её образа лежат на одной прямой.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание.

Утверждение задачи является частным случаем следующего факта.

Рассмотрим стереографическую проекцию сферы на плоскость из точки . Пусть — точка вне сферы , а окружность на , образованная касательными к из , не проходит через . Тогда образом будет окружность с центром в точке пересечения плоскости с лучом .

Так как плоскость перпендикулярна высота пирамиды лежит в грани Без ограничения общности можно считать, что сфера касается плоскости в точке лежащей на высоте (этого можно добиться, если выполнять перенос сферы параллельно плоскости основания пирамиды).

Пусть сфера касается плоскости в точке Докажем, что точки и лежат в одной плоскости и эта плоскость содержит . Пусть — центр сферы. — перпендикуляр к плоскости так как это отрезок на высоте пирамиды. — точка касания сферы и поэтому и перпендикулярны. Таким образом, и параллельны, поэтому лежат в одной плоскости (тогда и лежит в этой плоскости). так как эти отрезки являются основаниями трапеции Тогда плоскость параллельна прямой Докажем, что

Мы уже знаем, что Теперь заметим, что все три угла и — прямые, поэтому — прямоугольник. Тогда — перпендикуляр к плоскости так как и перпендикулярны. Таким образом, Тогда, действительно, и поэтому Точка лежит в плоскости Эта плоскость перпендикулярна при этом — прямая, перпендикулярная Тогда тоже лежит в плоскости

Ранее мы отмечали, что — прямоугольник. Так как — радиусы сферы, то на самом деле этот прямоугольник является квадратом. тогда — отрезки касательных. Пусть плоскость пересекает в точке

Пусть (эти отрезки действительно равны, как отрезки касательных). По теореме Пифагора для

Решаем это уравнение и получаем Теперь через точку проведем прямую параллельную причем и Тогда — это сечение пирамиды плоскостью Действительно, плоскость пересекает по прямой, параллельной при этом Поэтому, действительно, линия пересечения и параллельна поэтому совпадает с

Теперь по теореме Фалеса для углов и получаем: и аналогично

Продлим и до пересечения в точке

По условию поэтому точки и соответственно середины и Пусть Ясно, что Применяем теорему Менелая к и прямой

поэтому Пусть — объем пирамиды Пирамида имеет общую высоту с нашей пирамидой Треугольники и подобны с коэффициентом поэтому Тогда получаем, что причем — основание пирамиды если принять за ее вершину. По формуле объема пирамиды:

По теореме о пирамидах с общим трехгранным углом при вершине:

Таким образом, Снова по теореме о пирамидах с общим трехгранным углом при вершине:

Таким образом, Тогда — одна из частей, на которые плоскость разбивает исходную пирамиду Объем второй части равен Тогда требуемое по условию отношение равно

Пусть дана призма — центр данной сферы, которая касается боковых рёбер и в точках и

Заметим, что и следовательно А раз и все четыре точки лежат в одной плоскости, то и — прямоугольник, значит, при этом как диаметр данной сферы.

Рассмотрим треугольник и найдём высоту По формуле Герона тогда

Проецируем на нижнее основание, обозначим проекцию на она будет являться серединой Пусть — точка касания сферы с а — её проекция на нижнее основание.

Раз , то в силу ТТП и свойств проекции Тогда — средняя линия в треугольнике следовательно

Рассмотрим прямоугольную трапецию в ней и Пусть тогда по теореме Пифагора

Теперь зная это, посчитаем объём призмы

Пусть точка — основание высоты пирамиды, точка — центр описанной окружности сферы, — радиус этой сферы. Тогда По свойству правильной пирамиды точка лежит на прямой являющейся высотой.

Рассмотрим треугольник Он прямоугольный, так как перпендикулярна плоскости то есть перпендикулярна и прямой лежащей в как радиус окружности, описанной около правильного треугольника со стороной Рассмотрим, чему может быть равна длина отрезка в зависимости от положения точки относительно точек и

1.

Пусть лежит на отрезке Тогда

2.

Пусть лежит за точкой то есть точки и находятся по разные стороны от точки Тогда

3.

Пусть лежит за точкой то есть точки и находятся по разные стороны от точки Но тогда и в прямоугольном треугольнике катет больше чем гипотенуза что не возможно, то есть не может лежать за

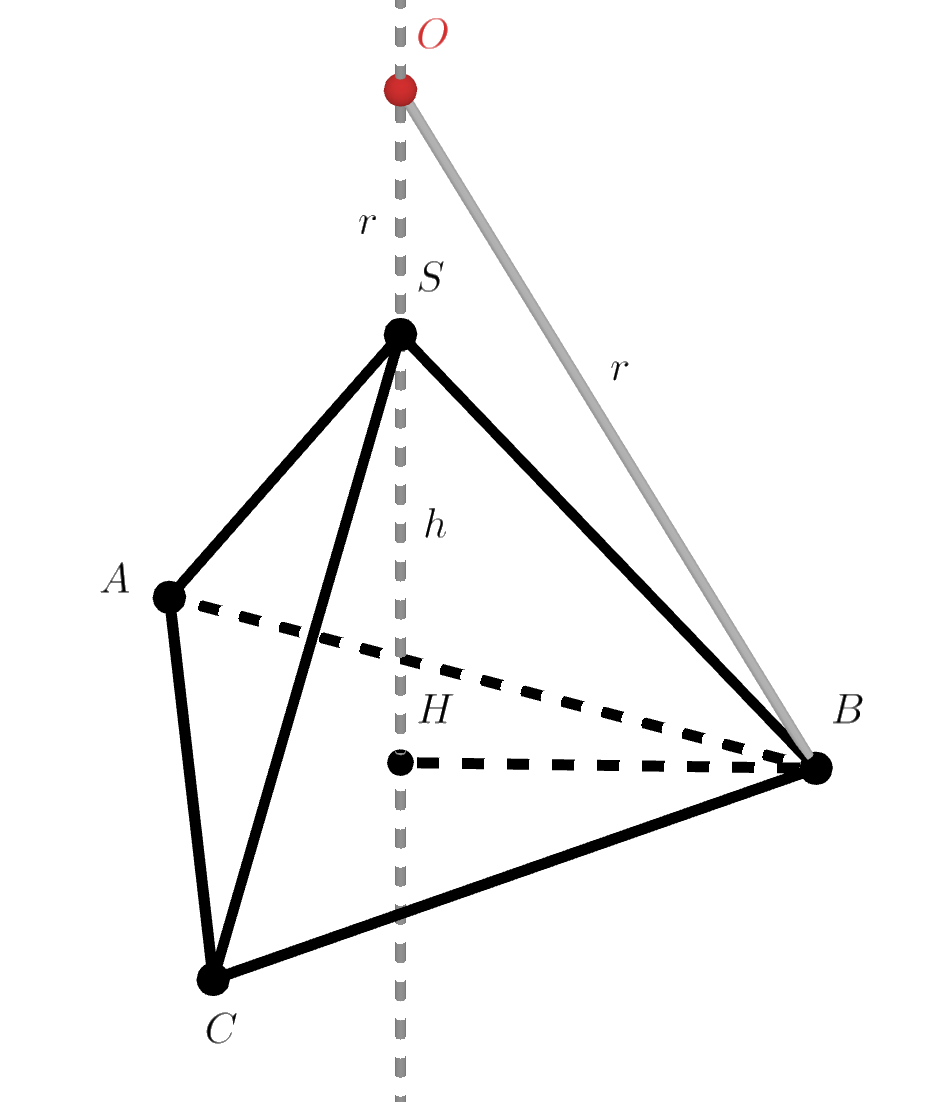
Получается, что По теореме Пифагора:

В силу симметрии центр вписанного в пирамиду шара будет лежать на высоте

Проведем аналогию с плоскостью. Центры вписанных шаров лежат на одной прямой и гомотетичны относительно точки Из гомотетии следует, что шар, вписанный в трёхгранный угол, будет касаться плоскости в точке, лежащей на следовательно, можно нарисовать треугольник

Точка касания шара, вписанного в пирамиду, с плоскостью лежит на высоте прямоугольника

С помощью этого мы можем узнать радиус. Рассмотрим треугольник в нём поэтому по теореме Пифагора. Теперь, чтобы узнать радиус шара, мы должны найти точку такую что будет равно перпендикуляру из к прямой Напишем уравнение, используя теорему Пифагора:

Следовательно, радиус шара, вписанного в пирамиду, будет равен

Вернемся к плоскости. Через подобие треугольников и найдем коэффициент подобия и найдем

Через диагональ и теорему Пифагора Через теорему Пифагора При этом

Пусть — треугольник, который служит основанием пирамиды, при этом Заметим, что то есть откуда — прямоугольный треугольник с гипотенузой

Все рёбра пирамиды равны, а значит, точки и равноудалены от четвёртой вершины пирамиды. Геометрическое место точек, равноудалённых от и — прямая, перпендикулярная плоскости и проходящая через центр окружности, описанной около

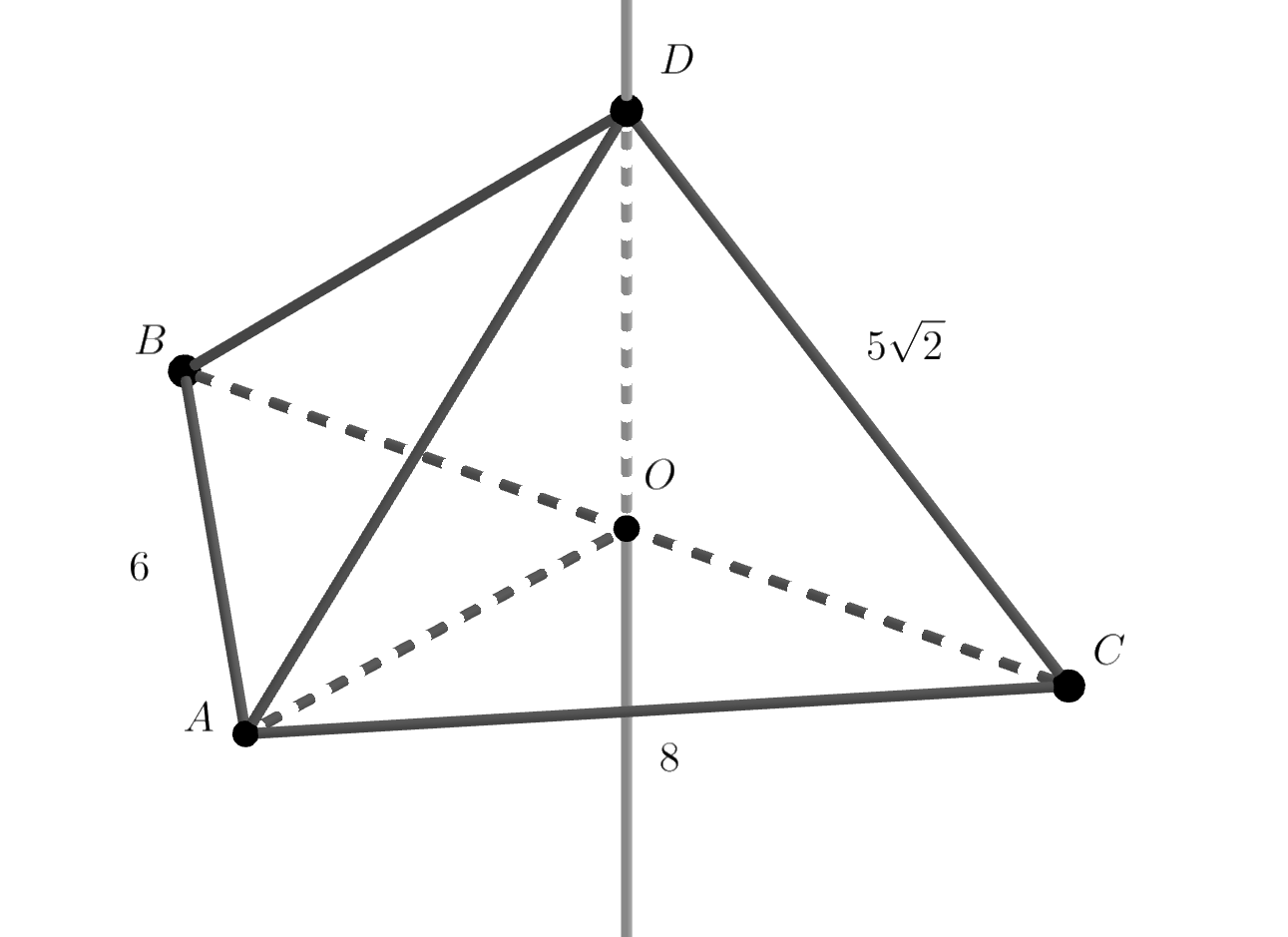
Так как треугольник — прямоугольный, то центр его описанной окружности лежит на середине его гипотенузы. Пусть точка — середина тогда вершина пирамиды лежит на прямой, перпендикулярной плоскости и проходящей через точку а так же

Треугольник — прямоугольный, так как прямая перпендикулярна плоскости то есть перпендикулярна и прямой лежащей в как ребро пирамиды, отсюда

Получается, то есть точка равноудалена от всех вершин пирамиды, откуда точка — центр описанной сферы. Значит, радиус описанной сферы равен 5.

а)

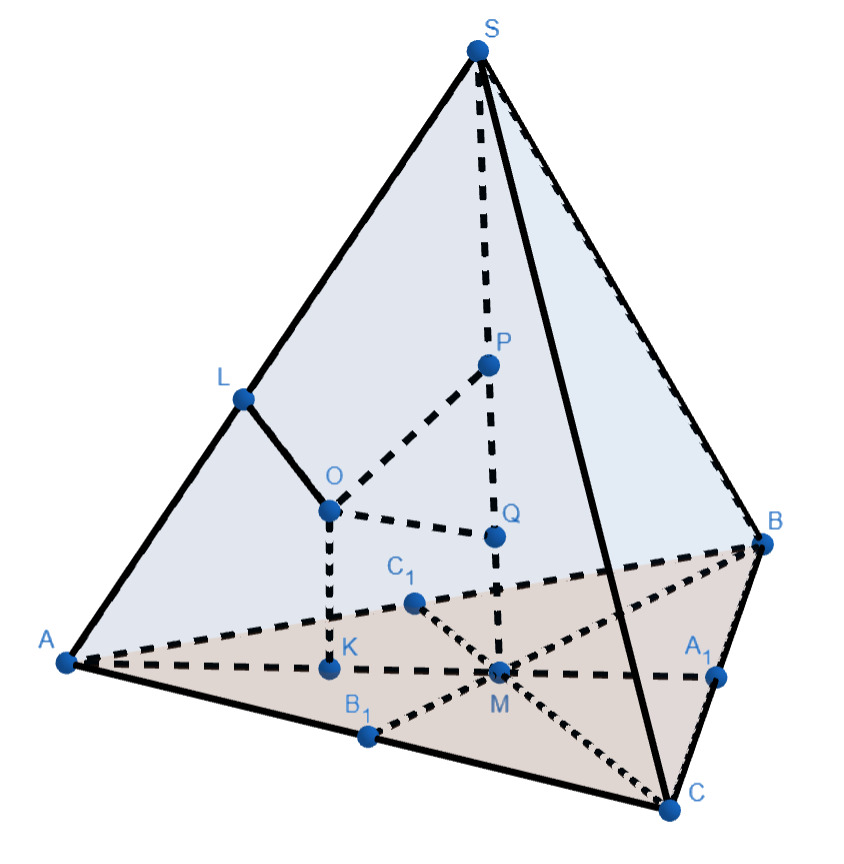
Поскольку — касательная к сфере а и — секущие к ней, то по теореме о касательной и секущей

Аналогично,

А поскольку то

В итоге получаем

Так как как касательные к сфере проведённые из точки то

А поскольку медианы треугольника точкой пересечения делятся в отношении считая от вершины, то

Кроме того,

При этом

то есть

Отсюда прямоугольный и Далее имеем

Значит,

б)

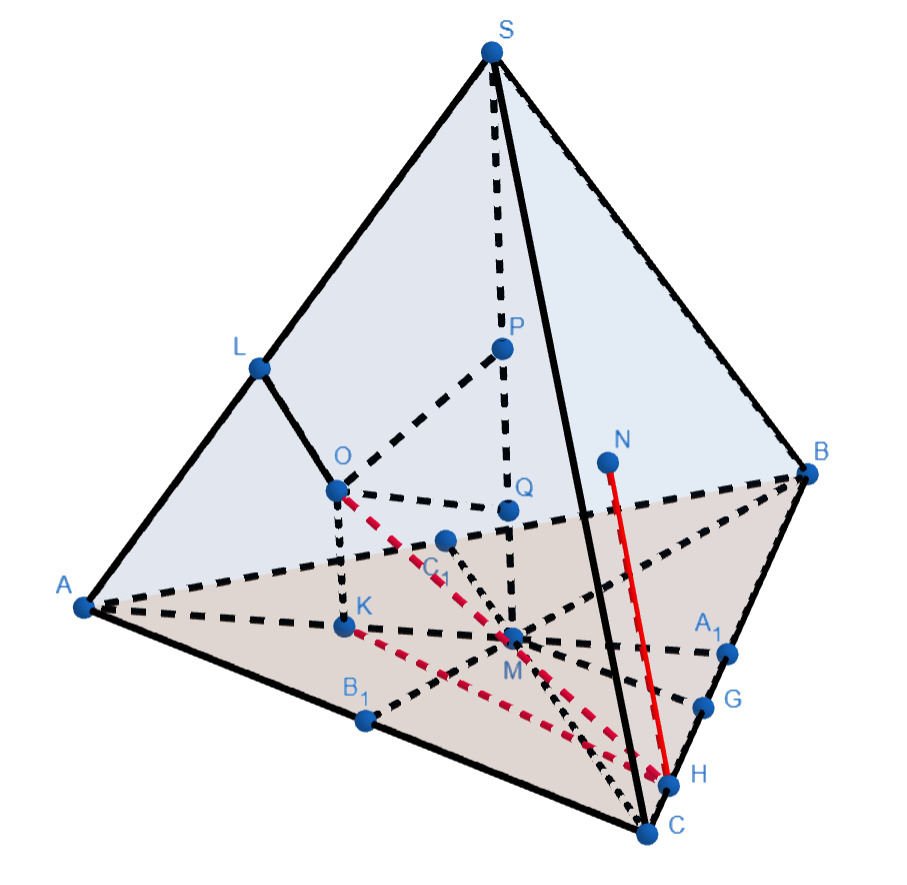
Пусть и — проекции точек и на прямую соответственно. Заметим, что потому что и — точки касания сферы со сторонами двугранного угла пирамиды при ребре Поэтому искомый угол равен

где — центр сферы

Далее имеем

Так как как касательные к то

Отсюда получаем

Из подобия и имеем

Окончательно,

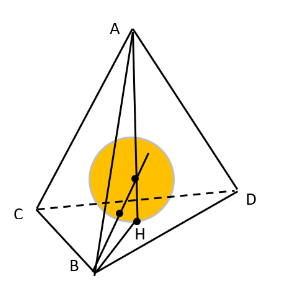
Рассмотрим тетраэдр удовлетворяющий условию задачи. Заметим, что по условию для любой высоты данного тетраэдра справедливо неравенство где — радиус вписанной сферы, то есть

Пусть — площадь грани, на которую опущена высота Докажем, что Предположим противное. Выберем грань минимальной площади (если таких граней несколько, то берём любую из них). Без нарушения общности можно считать, что её площадь равна (иначе можно ввести переобозначения). Так как не все равны между собой и - наименьшая из них, то

Выразим объём тетраэдра двумя способами:

Отсюда что противоречит неравенству

Итак, все равны, поэтому все равны, так как Обозначим за длину этих равных высот. Из приведённого выше соотношения для объёма получаем то есть неравенство обращается в равенство. Но это возможно только в случае, если высота содержит центр сферы и точку касания с гранью (и так для каждой высоты).

Пусть - основание высоты тетраэдра, опущенной из точки Тогда совпадает с точкой касания сферы и грани Пусть тогда по теореме о касательной и секущей По теореме Пифагора из прямоугольного треугольника получаем

Аналогично получаем такое же выражение для остальных рёбер тетраэдра, следовательно, они равны между собой, то есть тетраэдр правильный.

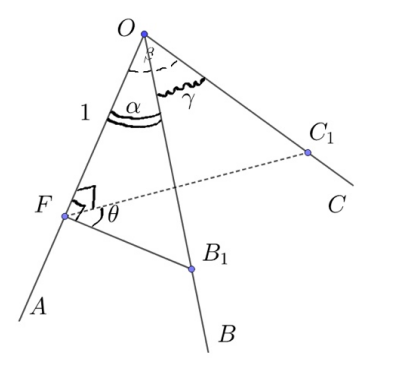
В задаче речь идет о трехгранном угле с вершиной в центре сферы, высекающем на сфере криволинейный треугольник. Площадь этого треугольника требуется выразить через радиус сферы и данные в условии плоские углы трехгранного угла, которые будем обозначать

Рассмотрим сначала две различные плоскости, проходящие через центр сферы. Пусть угол между этими плоскостями равен Плоскости пересекают сферу по большим окружностям. Касательные к окружностям в их точке пересечения также образуют угол Площадь поверхности сферы равна Площадь высекаемой плоскостями «дольки» (указанной на рисунке цветом) очевидно пропорциональна величине и равна

Три плоскости (содержащие грани трехгранного угла) разбивают сферу на треугольников. Искомую площадь криволинейного треугольника обозначим через а его углы (которые, очевидно, являются двугранными углами трехгранного угла за Площади криволинейных треугольников, примыкающих к сторонам треугольника обозначим С каждым из этих треугольников образует «дольку», поэтому Оставшиеся из -х нерассмотренных криволинейных треугольников симметричны -м рассмотренным относительно центра сферы. Значит, суммарная площадь рассматриваемых четырех треугольников равна половине площади сферы, то есть Тогда сложим первые три уравнения и воспользуемся четвертым:

Из теоремы косинусов для трехгранного угла

Отсюда получаем ответ.

Отметим на высоте пирамиды центр вписанной сферы. Также отметим середину стороны . Проведём перпендикуляр из точки на тогда , а точка — точка касания сферы с гранью . Тогда Поскольку , то , откуда с учётом (из свойств правильного треугольника) имеем

Отсюда заключаем

Замечание. Другим способом посчитать радиус является использование соотношения на площадь поверхности и объём пирамиды

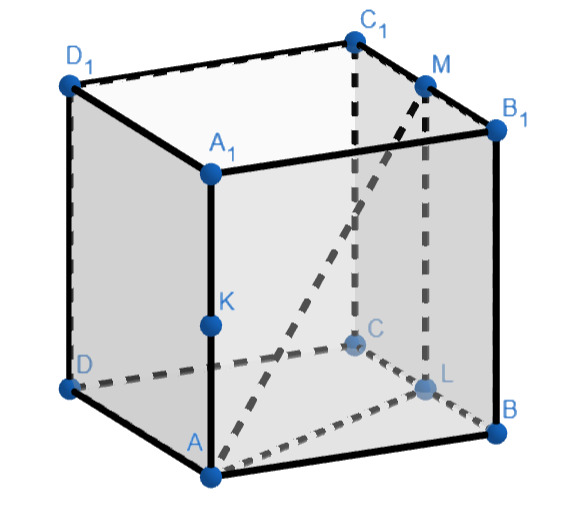
Пусть — середина ребра тогда Т.к. — куб, по теореме Пифагора из прямоугольного получаем

— середина а — середина следовательно, как средняя линия квадрата равна т.е. равна Т.к. — куб, по теореме Пифагора из прямоугольного получаем

Пусть — середина ребра тогда Т.к. сфера вписана в каркас куба значит, точками касания являются середины рёбер. Следовательно, используем теорему о касательной и секущей

Проведём сечение описанной композиции плоскостью, проходящей через центры трех сфер. Искомое расстояние будет длиной отрезка на этой плоскости.

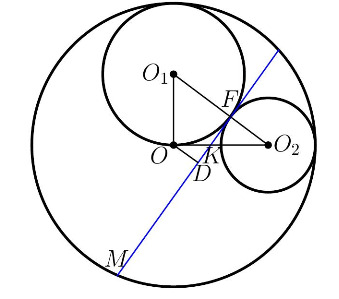
Пусть радиусы малых окружностей равны и Тогда радиус наибольшей (внешней) равен (дано: ). Рассмотрим Его стороны равны и следовательно, он прямоугольный.

Обозначим точку пересечения искомой хорды с отрезком через а с отрезком через Опустим из центра наибольшей окружности перпендикуляр на искомую хорду (отрезок общей касательной). Тогда искомая хорда делится точкой пополам и перпендикулярна отрезкам и

Прямоугольные треугольники подобны. Поэтому , откуда и

Далее, откуда

По теореме косинусов из треугольника находим, что

Пусть - высота треугольника . Тогда

С другой стороны,

Из уравнения находим, что По теореме о трёх перпендикулярах поэтому - линейный угол двугранного угла между плоскостями граней и Обозначим Из прямоугольного треугольника находим, что

Тогда

Пусть и - проекции центра сферы, описанной около пирамиды на плоскости граней и соответственно. Тогда и - центры описанных окружностей треугольников и Тогда, если - середина ребра то и
Поскольку центр описанной окружности треугольника и вершина лежат по разные стороны от прямой значит, центр сферы лежит внутри тупого двугранного угла, образованного плоскостями граней и
Рассмотрим сечение пирамиды плоскостью, проходящей через прямые и Прямая перпендикулярна этой плоскости, т.к. она перпендикулярна то точка также принадлежит этой плоскости. Заметим, что

поскольку центральный угол вдвое больше соответствующего вписанного. Из равнобедренных треугольников и находим, что

Прямоугольные треугольники и равны по гипотенузе и катету, поэтому а т.к. то Тогда

Пусть искомый радиус описанной сферы пирамиды Из прямоугольного треугольника находим, что

При таком расположении десяти одинаковых шаров центры четырёх из них расположены в вершинах правильного тетраэдра, а точки касания расположены на ребрах этого тетраэдра.

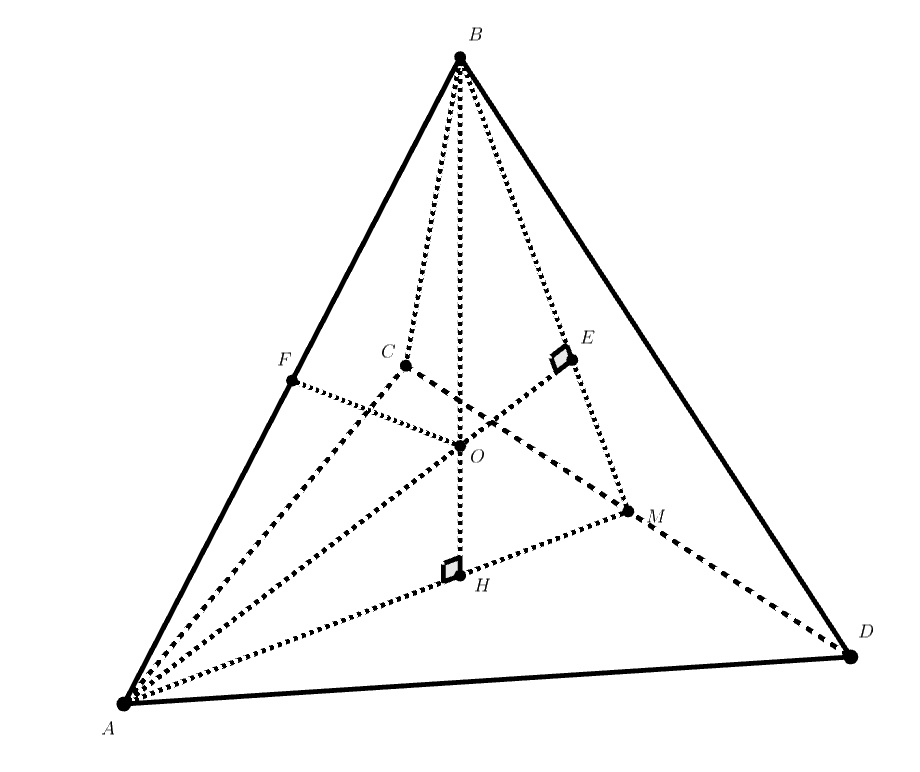
Следовательно, ребро тетраэдра равно четырём радиусам этих шаров, радиус внешней сферы больше радиуса шара, описанного около тетраэдра на четверть длины ребра тетраэдра, а радиус внутреннего шара меньше расстояния от центра тетраэдра до его грани на эту же величину. Рассмотрим сечение тетраэдра плоскостью :

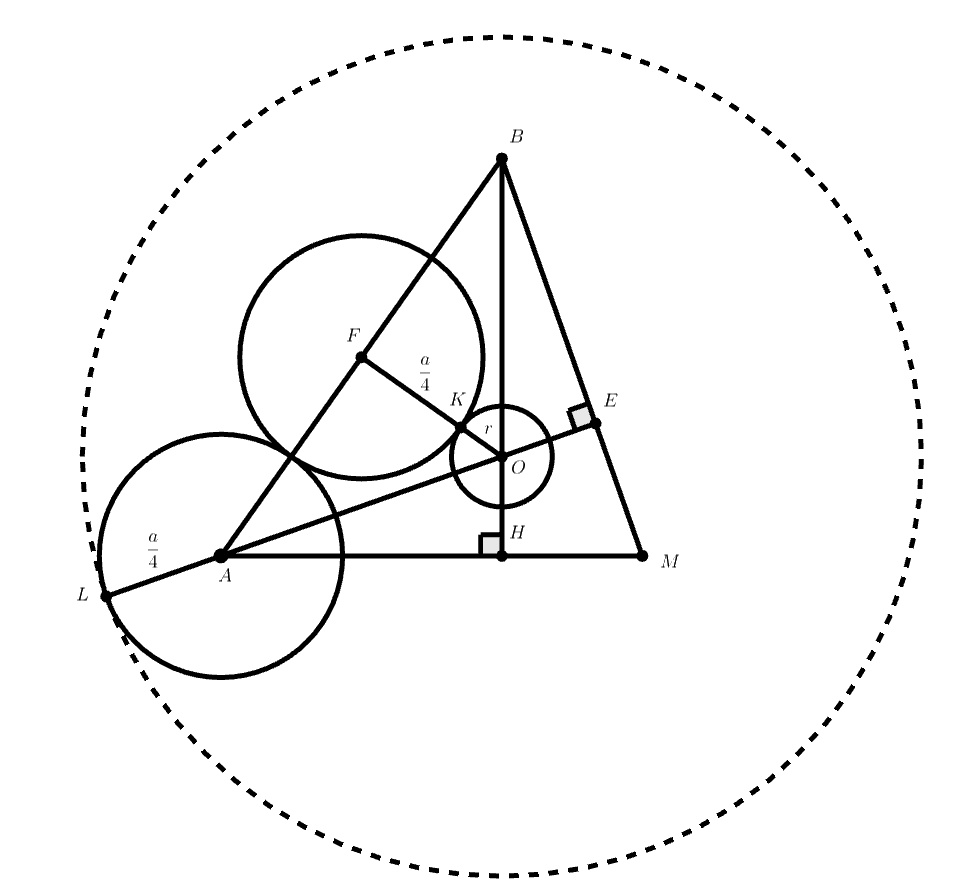
Обозначим длину ребра тетраэдра за , радиус сферы, описанной вокруг пирамиды из шаров за , радиус шара, вписанного в центр пирамиды из шаров за .

В треугольнике

следовательно,

Из подобия треугольников и имеем

В треугольнике :

следовательно,

Тогда

Таким образом,

откуда

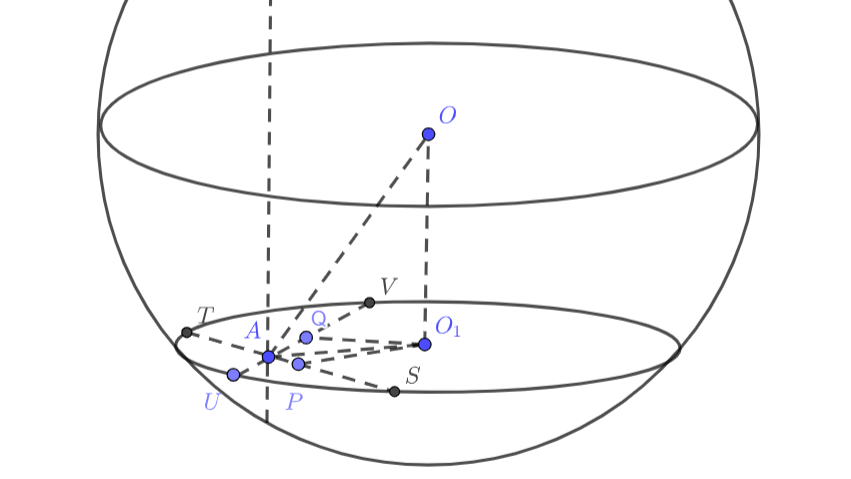
Первое решение.

Рассмотрим сечение шара, которое задаётся двумя пересекающимися в точке хордами и . Эта плоскость перпендикулярна каждой из плоскостей, заданных аналогично другими парами хорд, по признаку перпендикулярности плоскостей (каждая из них содержит прямую, перпендикулярную другой плоскости). Тогда они образуют “координатные плоскости” для осей прямоугольной системы координат, направленных вдоль хорд. По пространственной теореме Пифагора сумма квадратов проекций отрезка на оси равна квадрату длины отрезка , а сумма квадратов проекций отрезка на плоскости равна

Итак, рассматриваемое сечение шара является окружностью, обозначим её центр за . Известно, что перпендикуляры и из центра на хорды попадут в середины соответствующих хорд. Если обозначить , то по теореме Пифагора . Заметим, что как радиусы окружности. Если сложить равенства, получаем:

Учтём, что . Так как — проекция на плоскость, то складывая аналогичные равенства для двух других координатных плоскостей, получаем

Второе решение.

Рассмотрим прямоугольный параллелепипед, рёбра которого параллельны данным хордам, а точка и центр шара являются его противоположными вершинами. Пусть и - длины его рёбер; ясно, что a) Если хорда удалена на расстояние от центра шара, то квадрат её длины равен . Так как расстояния от данных хорд до точки равны диагоналям граней параллелепипеда, то искомая сумма квадратов равна