Тема СТЕРЕОМЕТРИЯ

Сферы

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела стереометрия

Разделы подтемы Сферы

Вписанная сфера

Описанная сфера

Сечение шара плоскостью

Касательные к сфере (+ каркасный тетраэдр)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 21#42960Максимум баллов за задание: 7

Докажите, что в любую треугольную пирамиду можно вписать единственную сферу.

Подсказки к задаче

Подсказка 1!

В стереометрии иногда полезно проводить аналогию с плоскостью, чтобы что-то придумать. Смотрите, у нас есть пирамида треугольная и вписанная сфера. Как аналогичное утверждение доказывается на плоскости? Да, что-то там про пересечение биссектрис...

Подсказка 2!

Рассмотрим биссекторы, содержащие ребра AB, BC, AC. Они пересекаются в одной точке, она равноудалена от сторон (проверьте!) Теперь осталось доказать, что второй такой точки еще не может быть!

Показать доказательство

Пусть эта пирамида $ABCD$ . Биссекторы, содержащие рёбра $AB,BC, AC$ , пересекаются в одной точке $O$ , которая находится на одинаковом расстоянии от всех четырёх граней, то есть является центром вписанной в пирамиду сферы. Если нашлась ещё одна сфера с центром $′ O$ , то она также обязана лежать в пересечении трёх биссекторов, но такая точка всего одна, поэтому сфера единственная.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 22#63890Максимум баллов за задание: 7

Дана правильная треугольная пирамида. Известно, что центр сферы, описанной около этой пирамиды, равноудалён от боковых рёбер и от плоскости основания пирамиды. Найдите радиус сферы, вписанной в эту пирамиду, если длина ребра её основания равна $12.$

Подсказки к задаче

Подсказка 1

Назовём нашу пирамиду SABC, где △ABC будет основанием. Попытаемся узнать длину бокового ребра, пользуясь данными о том, что центр описанной около этой пирамиды сферы равноудалён от боковых рёбер и плоскости основания. Где относительно высоты пирамиды будет расположен центр описанной сферы? Пусть Н — основание высоты, а О₁ — центр описанной сферы. Что можно сказать про △ASH, пользуясь тем, что точка О равноудалена от точки Н и прямой AS, а также от точек S и A?

Подсказка 2

Пирамида правильная, значит мы точно знаем положение точки Н, длину АН и отсюда сможем вытащить AS. Теперь мы знаем длины всех рёбер пирамиды! Подумайте, как можно вытащить радиус вписанной сферы?

Подсказка 3

Центр вписанной сферы О₂ также лежит на высоте пирамиды. Нетрудно доказать, что если М — середина АВ, то именно в плоскости (MSH) будут лежать радиусы, проведённые в точки касания сферы с гранями АВС и SAB. Рассмотрите △MSH, как мы можем в нём посчитать O₂H?

Подсказка 4

MH нетрудно ищется из свойств правильного треугольника. Пифагор поможет нам найти SM и SH. О₂, как точка равноудалённая от сторон МН и MS лежит на биссектрисе угла M. Осталось только применить свойство биссектрисы и задача решена!

Показать ответ и решение

Пусть $ABC$ — основание пирамиды, $S$ — вершина, $H$ — центр треугольника $ABC,$ $M$ — середина $AB,O 1$ — центр описанной сферы, $O2$ — центр вписанной сферы. Поскольку точка $O1$ равноудалена от $AS$ и $ABC,AO1$ — биссектриса треугольника $ASH.$ Стало быть, $∘ ∠HAO1 = ∠SAO1 = ∠ASO1 =30 .$

$PIC$

Поскольку $AB = 12,$ имеем $√- AH = 4 3,$ откуда $O1H =4,$ $O1A = O1S = 8.$ Для треугольника $MSH$ имеем $√- SH =12,MH = 2 3,$ откуда $√-- SM = 2 39.$ Поскольку $MO2$ — биссектриса, $√-- SO2 = HO2 ⋅SM∕MH =HO2 13.$ Стало быть, $√ -- HO2 (1 + 13)=$ $SH = 12,$ откуда $√-- HO2 = 13− 1.$

Ответ:

$√13-− 1$

Ошибка.
Попробуйте повторить позже

Задача 23#70779Максимум баллов за задание: 7

Дана пирамида $PQRS,$ вершина $P$ которой лежит на одной сфере с серединами всех её рёбер, кроме ребра $PQ.$ Известно, что $QR = 2,$ $QS = 1,$ $√- PS = 2.$ Найдите длину ребра $RS.$ Какой наименьший радиус может иметь сфера, описанная около данной пирамиды?

Источники: Физтех-2022, 11.7 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Во-первых, на что нам могут намекать середины сторон? На средние линии. А средние линии параллельны основаниям. Что мы можем из этого извлечь? Какие параллелограммы есть на картинке?

Подсказка 2

Во-первых, в силу свойства средней линии, ADCE и ABDP - параллелограммы. При этом они вписаны в сечения нашей сферой плоскостей ACD и PRS. А значит, эти параллелограммы - прямоугольники. А это дает много прямых углов, а значит - много перпендикулярностей. Какая прямая тогда перпендикулярна прямой RS? А что нам это дает?

Подсказка 3

Прямая PQ перпендикулярна прямой RS, из за того, что параллельные им прямые EA и AD перпендикулярны. Давайте опустим перпендикуляр QH на RS.

Подсказки 4

Тогда у нас плоскость QHP перпендикулярна RS. Значит, и прямая PH перпендикулярна RS. А значит, наш «согнутый» четырехугольник QRPS (то есть, мы можем повернуть треугольник QRS вокруг RS до момента, когда повернутый треугольник будет лежать в плоскости RPS) имеет взаимноперпендикулярные диагонали. А значит, две суммы квадратов противоположных сторон равны. А тогда мы нашли RP. А значит, у нас фиксированы две стороны прямоугольного треугольника RPS, и мы найдем его гипотенузу.

Подсказка 5

Остается дать оценку на радиус сферы, описанной вокруг тетраэдра. Ну какую самую глупую оценку можно дать? Что первое приходит в голову(с учетом того, что нам еще пример надо построить)?

Подсказка 6

Самая глупая оценка снизу - это то, что радиус не меньше радиуса описанной окружности треугольника QRS. Найти радиус нетрудно(мы знаем все три стороны). Остается привести пример.

Подсказка 7

Чтобы достигалось равенство, надо, чтобы у нас в плоскости QRS лежал содержался центр сферы. Впишем туда треугольник QRS.

Подсказка 8

Остается доказать, что на сфере найдется точка P’, такая, что треугольники PRS и P’RS равны(это по сути и значит, что получен тетраэдр, который подходит под условия). То есть по сути надо поворачивать треугольник P’RS, равный треугольнику PRS, вокруг RS, до того момента, как точка P’ не станет принадлежать окружности.

Показать ответ и решение

Пусть $A,B,C,D,E$ - середины рёбер $PR,RS,QS,PS,QR$ соответственно. Из теоремы о средней линии треугольника следует, что $ADCE$ и $ABDP$ - параллелограммы. Они вписаны в окружности, являющиеся сечениями сферы плоскостями $ACD$ и $PRS$ , поэтому эти параллелограммы - прямоугольники. Угол $RP S$ — прямой; прямые $PQ$ и $RS$ перпендикулярны, так как $P Q∥AE, AE ⊥CE, CE ∥RS.$

Отметим в плоскости $PRS$ точку $′ Q$ такую, что $′ △QRS = △Q RS,$ а точки $P$ и $′ Q$ лежат по разные стороны от прямой $RS$ (треугольник $′ QRS$ может быть получен из треугольника $QRS$ поворотом вокруг прямой $RS).$

$PIC$

Из равенства треугольников $QRS$ и $Q′RS$ следует, что основания их высот, опущенных на $RS$ — это одна и та же точка (назовём её $H ).$ Плоскость $HQQ ′$ перпендикулярна $RS$ (так как $QH ⊥ RS,Q′H ⊥ RS),$ поэтому $QQ′ ⊥ RS.$ Поскольку $QQ ′ ⊥ RS$ и $PQ ⊥ RS,$ то плоскость $P QQ′$ перпендикулярна $RS$ и $PQ ′ ⊥RS.$

Значит, диагонали четырёхугольника $PRQ ′S$ пересекаются под прямым углом (в точке $H$ ). По теореме Пифагора

PR2 =P H2+ RH2,Q′R2 = Q′H2+ RH2,

Q′S2 =Q ′H2 +SH2,P S2 = PH2+ SH2

Следовательно,

P S2+ Q′R2 = PR2+ Q′S2

∘------------- PR = 22+ (√2)2− 12 = √5

Из прямоугольного треугольника $PRS$ находим

∘---2----2 √- RS = PR +P S = 7

Радиус сферы, описанной около пирамиды $PQRS$ , не меньше радиуса $r$ окружности, описанной около грани $QRS$ . Пирамида, для которой достигается равенство, существует. Докажем это.

$PIC$

Рассмотрим сферу радиуса $r$ и окружность - её сечение, проходящее через центр сферы. В сечении сферы указанной плоскостью получится окружность с диаметром $RS$ , в которую можно вписать прямоугольный треугольник $PRS$ . По теореме косинусов из треугольника $PRS$ находим, что

QR2+ QS2− RS2 4+1 − 7 1 cos∠RQS = --2⋅QR-⋅QS----= 2-⋅2-⋅1--=− 2

∠RQS =120∘

По теореме синусов

RS √7- r = 2sin∠RQS-= √3-

Ответ:

$RS = √7,R =∘ 7- min 3$

Ошибка.
Попробуйте повторить позже

Задача 24#90553Максимум баллов за задание: 7

Даны четыре точки $A,B,C,D$ , не лежащие в одной плоскости. Сфера касается прямых $AB$ и $AD$ в точке $A$ , а прямых $BC$ и $CD$ в точке $C.$ Найдите радиус сферы, если известно, что $AB =1,BD = 2$ и углы $ABC$ и $BAD$ прямые.

Показать ответ и решение

Касательные, проведенные из одной точки к сфере, равны. Значит, $DA = DC$ и $BA = BC$ . Следовательно, треугольники $ABD$ и $BCD$ равны по трем сторонам.

Угол $BAD$ прямой, так что высота $AK$ треугольника $BAD$ , опущенная из вершины $A$ , попадает на сторону $BD.$ Из равенства треугольников $ABD$ и $BCD$ следует, что $CK ⊥BD$ . Ясно, что плоскость $ACK$ содержит центр $O$ сферы.

$PIC$

В прямоугольном треугольнике $ABD$ известны катет $AB = 1$ и гипотенуза $BD = 2.$ Отсюда легко найти, что $√- AD = √3,AK = 23$ . Из теоремы Пифагора для треугольника $ABC$ находим, что $AC =√2$ (ибо $AB = BC =1$ , а угол $ABC$ по условию прямой). Кроме того, из $AE = EC$ следует, что $√- AE = 22.$

В прямоугольном треугольнике $OAK$ мы нашли катет $AK$ и высоту $AE$ . Осталась тривиальная планиметрическая задача нахождения катета $OA$ , равного радиусу сферы.

Ответ:

$∘ 3 2$

Ошибка.
Попробуйте повторить позже

Задача 25#91394Максимум баллов за задание: 7

Сфера касается всех рёбер пирамиды $SABC$ , причём боковых рёбер $SA,SB$ и $SC$ — в точках $A′,B ′$ и $C′.$ Найдите объём пирамиды $′′ ′ SA B C$ , если $AB = BC = SB =5$ и $AC = 4.$

Показать ответ и решение

$PIC$

Поскольку сфера касается всех рёбер, пирамида обладает тем свойством, что $BC +AS = AB+ SC = AC+ SB = 9$ , откуда получаем $AS = SC = 4$ , следовательно, треугольник $ASC$ равносторонний. Тогда треугольник $A′SC′$ тоже равносторонний, поэтому $SA ′= SC ′=$ $A ′C′ = 2$

Найдём объём пирамиды $SABC$ как правильной пирамиды с основанием $SAC :$

√-- VSABC = 4-59 3

Поскольку

VSA′B′C-′ SA′⋅SB′⋅SC′ VSABC = SA⋅SB ⋅SC

окончательно получаем

√-- VSA′B′C′ = 110VSABC = 21559

Ответ:

$2√59 15$

Ошибка.
Попробуйте повторить позже

Задача 26#98163Максимум баллов за задание: 7

В сферу радиуса $3$ вписана правильная треугольная призма $ABCA B C 1 1 1$ с основанием $ABC$ и боковыми ребрами $AA ,BB ,CC . 1 1 1$ Отрезок $CD$ — диаметр этой сферы. Найти объем призмы, если $√- AD = 2 6.$

Источники: Газпром - 2022, 11.6 (см. olympiad.gazprom.ru)

Подсказки к задаче

Подсказка 1

Нам нужно понять, от чего зависит конструкция, то есть какими параметрами задаётся. С учетом того, что нам надо найти объём, то есть найти площадь основания на высоту, какие параметры нам удобно ввести, чтобы через них всё выражалось?

Подсказка 2

Удобно ввести высоту и радиус окружностей, в которые вписано каждое из оснований. Тогда, поскольку в силу симметрии CD — диаметр, то нам известна длина CD, а также известна длина AD. Это значит, что у нас есть два уравнения на две переменных (r и h), поскольку есть два прямоугольных треугольника у которого стороны либо константы, либо выражаются через r и h. Осталось решить такую систему и посчитать объём!

Показать ответ и решение

Плоскости оснований $ABC$ и $A B C 1 1 1$ призмы пересекают сферу по окружностям, описанным около правильных треугольников $ABC$ и $A1B1C1;$ пусть их центры — точки $O$ и $O1$ соответственно.

Легко показать, что середина $M$ отрезка $OO1$ является центром сферы.

$PIC$

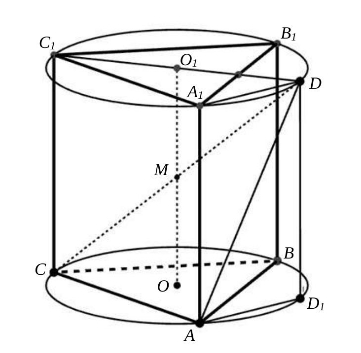
Проведем через точку $C1$ диаметр $C1D$ окружности с центром в точке $O1.$ Покажем, что $CD$ — диаметр сферы. Действительно, плоскость $CC1D$ перпендикулярна плоскостям основания и, значит, вместе с точкой $O1$ содержит отрезок $OO1.$ Т.к. $C1D = 2DO1,$ прямая $CD$ пересекает отрезок $OO1$ в его середине, т.е. в центре $M$ заданной сферы.

Пусть $D1$ — проекция точки $D$ на плоскость основания $ABC,$ высота призмы равна $h,$ а радиусы окружностей с центрами $O$ и $O1$ равны $r.$ Рассмотрим треугольники $CC1D$ и $ADD1.$ Учитывая, что $C1D = 2r,AD1 =r$ (треугольник $AOD1$ равносторонний), $CC1 = DD1 =h,$ по т. Пифагора получаем систему уравнений:

{ h2+4r2 = 62√ h2+r2 =(2 6)2

Решая систему, находим, что $√- r= 2,h =2 5.$ Тогда сторона основания равна $√ - 2 3,$ его площадь $√ - S =3 3,$ и следовательно, объем призмы $√-- V = S⋅h =6 15.$

Ответ:

$6√15$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 27#63815Максимум баллов за задание: 7

Дан тетраэдр $ABCD$ . Известно, что центр сферы, описанной около этого тетраэдра, лежит на $AB$ , что плоскости $ABC$ и $ABD$ перпендикулярны и что $AD =DC = CB$ . Найдите угол между прямыми $AD$ и $CB.$

Источники: ДВИ - 2021, вариант 214, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть К — центр описанной сферы. Отметьте равные отрезки-радиусы сферы. Какой вывод можно сделать, смотря на △ADB и его медиану, равную половине стороны? Какой вывод можно сделать о △АВС?

Подсказка 2

Итак, перед нами два прямоугольных треугольника с общей гипотенузой и равными катетами, значит они сами...? Проведите высоту DH в △ADB, что можно сказать об отрезке СН, пользуясь перпендикулярностью плоскостей?

Подсказка 3

Из равенства треугольников можно вывести, что ВН = АН, то есть Н совпадает с К, значит △ADB и △AСB не только прямоугольные, но и...?

Подсказка 4

Отметьте L и M — середины рёбер BD и CD соответственно. Что можно сказать о связи LM и BC? А о LK и AD? Осталось внимательно рассмотреть △MLK и записать ответ!

Показать ответ и решение

Сразу отметим, что, поскольку центр сферы, описанной около тетраэдра, лежит на $AB$ , углы $ACB$ и $ADB$ - прямые.

$PIC$

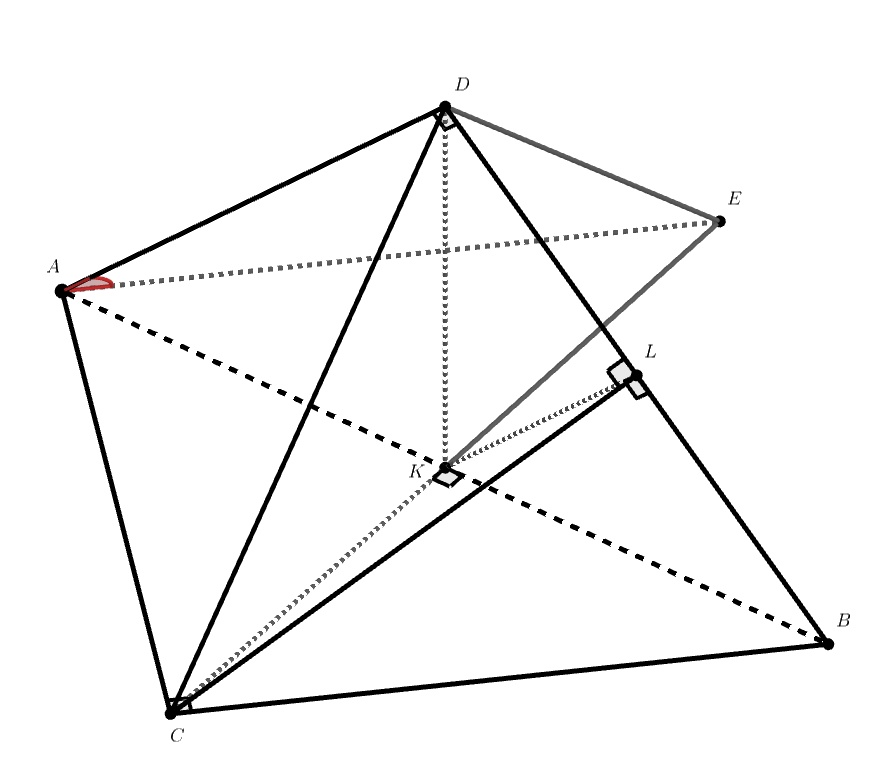
Далее, опустим перпендикуляры $CK$ и $CL$ на $AB$ и $BD$ соответственно. Тогда $DL = LB$ , ибо $DC = CB$ , следовательно, $KL −$ серединный перпендикуляр к $BD$ в плоскости $ABD$ и, поскольку $∘ ∠ADB = 90$ , точка $K$ является серединой $AB$ . Значит, $AC =BC$ . Аналогично, $AD = BD.$

Итак, $AC = BC = AD =BD =CD, AB ⊥CK, AB ⊥DK, AK = BK = CK =DK$ . Пусть $E −$ точка, симметричная точке $C$ относительно $K$ . Тогда $AK ⊥ EK ⊥ DK$ и $AK = EK =DK$ . Следовательно, треугольник $ADE −$ равносторонний. При этом $AE ∥CB$ . Стало быть, искомый угол равен углу $EAD$ и равен $60∘.$

Ответ:

$60∘$

Ошибка.
Попробуйте повторить позже

Задача 28#63816Максимум баллов за задание: 7

Дан параллелепипед $ABCDA ′B′C′D′$ с основаниями $ABCD, A ′B′C′D′$ и боковыми рёбрами $AA ′,BB′,CC′,DD ′.$ Все рёбра параллелепипеда равны. Плоские углы при вершине $B$ также равны. Известно, что центр сферы, описанной около тетраэдра $′ ′ AB CD ,$ лежит в плоскости $′ AB C.$ Радиус этой сферы равен $2.$ Найдите длину ребра параллелепипеда.

Источники: ДВИ - 2021, вариант 216, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

В вершине В сходятся 3 равных угла, что можно сказать об отрезках-диагоналях граней, лежащих напротив этой вершины? (Строго обосновать этот факт можно через треугольники, равные по 2-м сторонам и углу между ними!)

Подсказка 2

В какой ещё из вершин параллелепипеда сходятся 3 равных угла? Какой вывод можно сделать об отрезках-диагоналях граней, исходящих из этой же вершины?

Подсказка 3

Каким свойством в таком случае обладает тетраэдр D'AB'C: у него равны боковые рёбра и в основании лежит правильный треугольник? Таким образом мы можем вычислить все его стороны!

Подсказка 4

Восстановите длину стороны ромбов-граней по найденным диагоналям и можно записывать ответ!

Показать ответ и решение

$PIC$

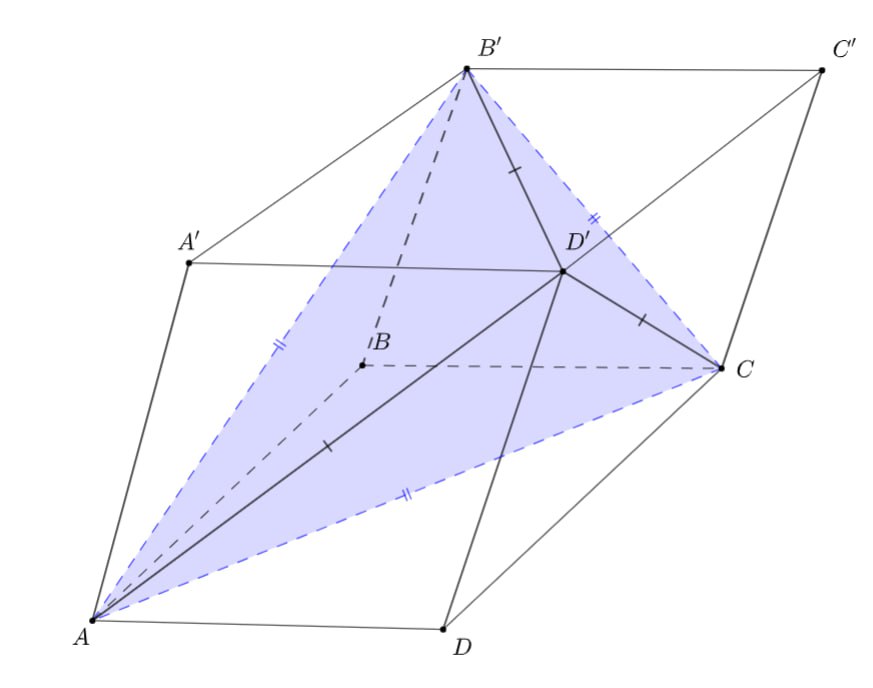
Грани параллелепипеда являются ромбами. Поскольку плоские углы при вершине $B$ равны, равны также и плоские углы при вершине $D ′$ . Стало быть, $AD′ = B′D′ = CD ′$ как равные диагонали ромбов и, по той же причине, $AB ′ = B′C = AC$ . Таким образом, центр сферы, описанной около тетраэдра $AB′CD′$ , является центром окружности, описанной около правильного треугольника $AB′C$ , а также является основанием высоты тетраэдра, опущенной из вершины $D′$ . Отсюда получаем $√ - √ - AB ′ =2 3,AD ′ =2 2$ . Итак, диагонали ромба равны $- 2√ 3$ и $- 2√ 2$ , значит, его сторона равна $- √ 5.$

Ответ:

$√5$

Ошибка.
Попробуйте повторить позже

Задача 29#63818Максимум баллов за задание: 7

Вписанная в треугольную пирамиду $ABCD$ сфера касается граней $BCD, ACD,ABD$ и $ABC$ в точках $A ,B ,C 1 1 1$ и $D 1$ соответственно. Известно, что $D1$ является точкой пересечения высот треугольника $ABC$ , что плоскости $ABC$ и $A1B1C1$ параллельны и что радиус окружности, описанной около треугольника $ABC$ в четыре раза больше радиуса окружности, описанной около треугольника $A1B1C1$ . Найдите отношение, в котором сфера делит отрезок $DD1$ , считая от вершины $D.$

Источники: ДВИ - 2021, вариант 213, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

В задаче фигурирует ортоцентр, это явно неспроста. Пусть А2, B2, C2 - вершины ортотреугольника и О - центр сферы. Что можно заметить?

Подсказка 2

Представляют интерес четырехугольники OA1A2D1, OB1B2D1, OC1C2D1. На какие фигуры их можно разбить?

Подсказка 3

Они разбиваются на равные прямоугольные треугольники! Можем поотмечать равные углы и затем отметить равные отрезки.

Подсказка 4

В итоге имеем, что D1 - точка пересечения биссектрис АВС. Что тогда можем сказать?

Подсказка 5

ABC - правильный треугольник! (так как его ортоцентр совпал с инцентром) Тогда мы можем сказать какая прямая является высотой пирамиды.

Подсказка 6

Остается провести радиусы окружностей из условия и в вспомогательной плоскости поработать с нашей конструкцией.

Показать ответ и решение

Пусть $O$ — центр сферы и пусть $A ,B ,C 2 2 2$ — основания высот треугольника $ABC$ , опущенных из вершин $A,B,C$ соответственно.

$PIC$

Рассмотрим четырёхугольники $OA1A2D1$ , $OB1B2D1,OC1C2D1$ . Каждый из них состоит из двух равных прямоугольных треугольников. При этом катеты $OD1,OA1,OB1, OC1$ равны.

Из равенства расстояний от $A1,B1,C1$ до плоскости $ABC$ следует, что равны углы $D1OA1,D1OB1,D1OC1$ , а стало быть, равны и углы $D1A2A1$ , $D1B2B1,D1C2C1$ . Значит, равны отрезки $D1A2,D1B2,D1C2$ , то есть $D1$ является точкой пересечения биссектрис треугольника $ABC$ . При этом $D1$ это ортоцентр $ABC$ . Стало быть, треугольник $ABC$ правильный. Поскольку углы $D1A2A1,D1B2B1,D1C2C1$ равны, $DD1$ — высота пирамиды. Опустим из $A1$ перпендикуляр $A1D2$ на $DD1$ . Тогда радиус окружности, описанной около треугольника $A1B1C1$ равен $A1D2$ . Радиус же окружности, описанной около треугольника $ABC$ равен $AD1$ . Получаем, что $A2D1 = 1AD1 = 1 ⋅4A1D2 = 2A1D2 2 2$ . Отсюда видим, что $∠D1A2A1 = 60∘$ . Стало быть, $DD1 = √3⋅A2D1 = √3⋅√3⋅OD1 = 3OD1$ . Получаем, что искомое отношение равно $(DD1 − 2OD1 ):2OD1 = 1:2.$

Ответ:

$1 :2$

Ошибка.
Попробуйте повторить позже

Задача 30#63819Максимум баллов за задание: 7

Сфера касается всех рёбер тетраэдра $ABCD$ . Известно, что произведения длин скрещивающихся рёбер равны. Известно также, что $AB = 3,BC = 1$ . Найдите $AC.$

Источники: ДВИ - 2021, вариант 215, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Подумаем, как можно применить условие о том, что сфера касается всех рёбер тетраэдра? Более всего с длинами рёбер тут связывается свойство касательных: отрезки касательных к сфере, проведенных из одной точки, равны! Обозначьте одной буквой все равные отрезки проведённые из каждой из вершин и при помощи этих букв запишите равенство произведений длин скрещивающихся рёбер. ---

Подсказка 2

Поработайте теперь с нашим двойным равенством: рассмотрите две пары уравнений и попробуйте их преобразовать. Какие интересности связанные с отрезками касательных из разных вершин можно заметить?

Подсказка 3

Если сделать всё аккуратно, то получится несколько вариантов: равны либо отрезки касательных проведённые из вершин А и С, либо проведённые из вершин В и D. Рассмотрите оба случая, не выходит ли в одном из них противоречий с условием задачи? (Не зря же нам даны AB и BC). Аналогично рассмотрите вторую пару вершин, отрезки касательных из которых равны. Останется лишь внимательная арифметика и АС откроется нам!

Показать ответ и решение

Расстояния от вершины $A$ до точек касания сферы с рёбрами $AB,AC,AD$ равны. Обозначим это расстояние $a$ . Соответствующие расстояния от вершин $B,C,D$ обозначим $b,c$ , $d$ соответственно.

$PIC$

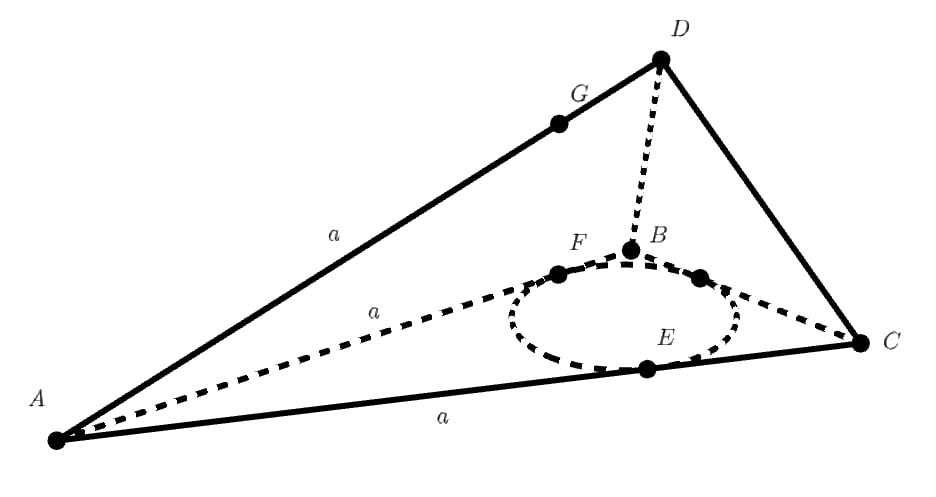
По условию $(a+b)(c+ d)= (a+ c)(b+ d)=(a+ d)(b+ c)$ , что равносильно после раскрытия скобок системе

(a− c)(b− d)= 0 и (a − b)(c− d)= 0.

Если $a= c$ , то $AB =BC$ , а это не так. Значит, $b= d$ . Тогда либо $a= b$ , либо $c =b$ . Если $a =b$ , то $AC = BC = 1$ , что противоречит неравенству треугольника. Значит, $c=b$ и, стало быть, $AC =AB = 3.$

Замечание.

Тетраэдр, у которого произведения длин скрещивающихся рёбер равны, называется каркасным, можете поизучать его свойства. В задаче по сути просили доказать, что у такого тетраэдра суммы длин скрещивающихся рёбер равны.

Ответ:

$3$

Ошибка.
Попробуйте повторить позже

Задача 31#71956Максимум баллов за задание: 7

В пирамиде $SA A ...A 1 2 n$ все боковые рёбра равны. Точка $X 1$ — середина дуги $A A 1 2$ описанной окружности треугольника $SA A , 1 2$ точка $X2$ — середина дуги $A2A3$ описанной окружности треугольника $SA2A3$ и т. д., точка $Xn$ — середина дуги $AnA1$ описанной окружности треугольника $SAnA1.$ Докажите, что описанные окружности треугольников $X1A2X2,X2A3X3,...,XnA1X1$ пересекаются в одной точке.

$PIC$

Источники: СпбОШ - 2021, задача 11.3(см. www.pdmi.ras.ru)

Подсказки к задаче

Подсказка 1:

Давайте поймем, поизучаем сферу, описанную вокруг данной фигуры. Во-первых, почему вообще можно описать сферу? Во-вторых, где у неё центр?

Подсказка 2:

Вокруг многоугольника A₁A₂...Aₙ можно описать окружность, значит, вокруг всей фигуры можно описать сферу. Пусть центр сферы — это точка P. Она равноудалена от точек A, следовательно, лежит на прямой, перпендикулярной плоскости основания и проходящей через S. Что мы можем сказать про точки X? Где они лежат?

Подсказка 3:

Они тоже лежат на этой сфере! Давайте попробуем угадать, где может находиться искомая точка. Попробуйте нарисовать фигуру и провести окружности.

Подсказка 4:

Давайте попробуем доказать, что искомая точка пересечения диаметрально противоположна S. Тогда нужно доказать, что N, X(k−1), X(k) и A(k) лежат на одной плоскости. Как это можно сделать?

Подсказка 5:

Воспользуемся тем, что N диаметрально противоположна S. Тогда угол SA(k)N прямой при всех A(k). Какие ещё углы равны 90 градусам?

Подсказка 6:

Углы SA(k)X(k) прямые, потому что S и X(k) диаметрально противоположны в окружности, описанной вокруг треугольника SA(k)X(k). Тогда SA перпендикулярно какой плоскости? Какие точки на ней лежат?

Показать доказательство

Заметим, что точки $A ,A ,...,A 1 2 n$ лежат и на сфере с центром в точке $S,$ и в одной плоскости. Следовательно, они лежат на окружности $ω,$ являющейся пересечением сферы с плоскостью. Пусть $O$ — центр этой окружности. Тогда $SO$ перпендикулярно плоскости основания и любая точка на прямой $SO$ равноудалена от всех точек окружности $ω.$ Поэтому на $SO$ найдётся и такая точка $P,$ для которой $P S = PA1.$ Тогда на сфере $σ$ с центром в точке $P$ и радиусом $PS$ лежат все вершины пирамиды, а также все окружности $SAkAk+1.$

$PIC$

Следовательно, на этой сфере лежат все точки $Ak$ и $Xk.$ Пусть $N$ — точка на сфере $σ,$ диаметрально противоположная точке $S.$ Покажем, что описанные окружности треугольников $Xk− 1AkXk$ проходят через точку $N.$ Поскольку точки $N, Xk−1,Xk$ и $Ak$ лежат на сфере, достаточно проверить, что они лежат в одной плоскости. Эта плоскость перпендикулярна прямой $SAk$ и проходит через точку $Ak.$ В самом деле, $∠SAkN = 90∘,$ поскольку они опирается на диаметр $SN$ сферы $σ,∠SAkXk =90∘$ и $∠SAkXk −1 = 90∘,$ поскольку они опираются на диаметры $SXk$ и $SXk −1$ описанных окружностей треугольников $SAkXk$ и $SAkXk −1.$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 32#96829Максимум баллов за задание: 7

Около шара радиуса $1$ описана правильная $n$ -угольная призма, все ребра которой касаются некоторого другого шара. Докажите, что $n =4$ и найдите объём этой призмы.

Источники: Миссия выполнима - 2021, 11.6 (см. www.fa.ru)

Подсказки к задаче

Подсказка 1

В этой задаче самое главное — связать боковую сторону и сторону многоугольника основания. Так как в основании у нас правильный многоугольник, в который вписана окружность радиуса 1, то чему в этом случае равна сторона основания? А какой факт можно извлечь из того, что вторая сфера касается каждого ребра?

Подсказка 2

В этом случае, сторона равна 2tg(pi/n) — просто опускаем высоту из центра на какую-нибудь сторону и вычисляем. А вот из того, что вторая сфера касается каждого ребра, следует, что прямоугольник боковой стороны является описанным. Осталось связать этот факт и тот, что в призму вписана сфера с радиусом 1, и получим ответ!

Показать ответ и решение

Высота призмы и боковое ребро равны $2$ (диаметру вписанного шара).

$PIC$

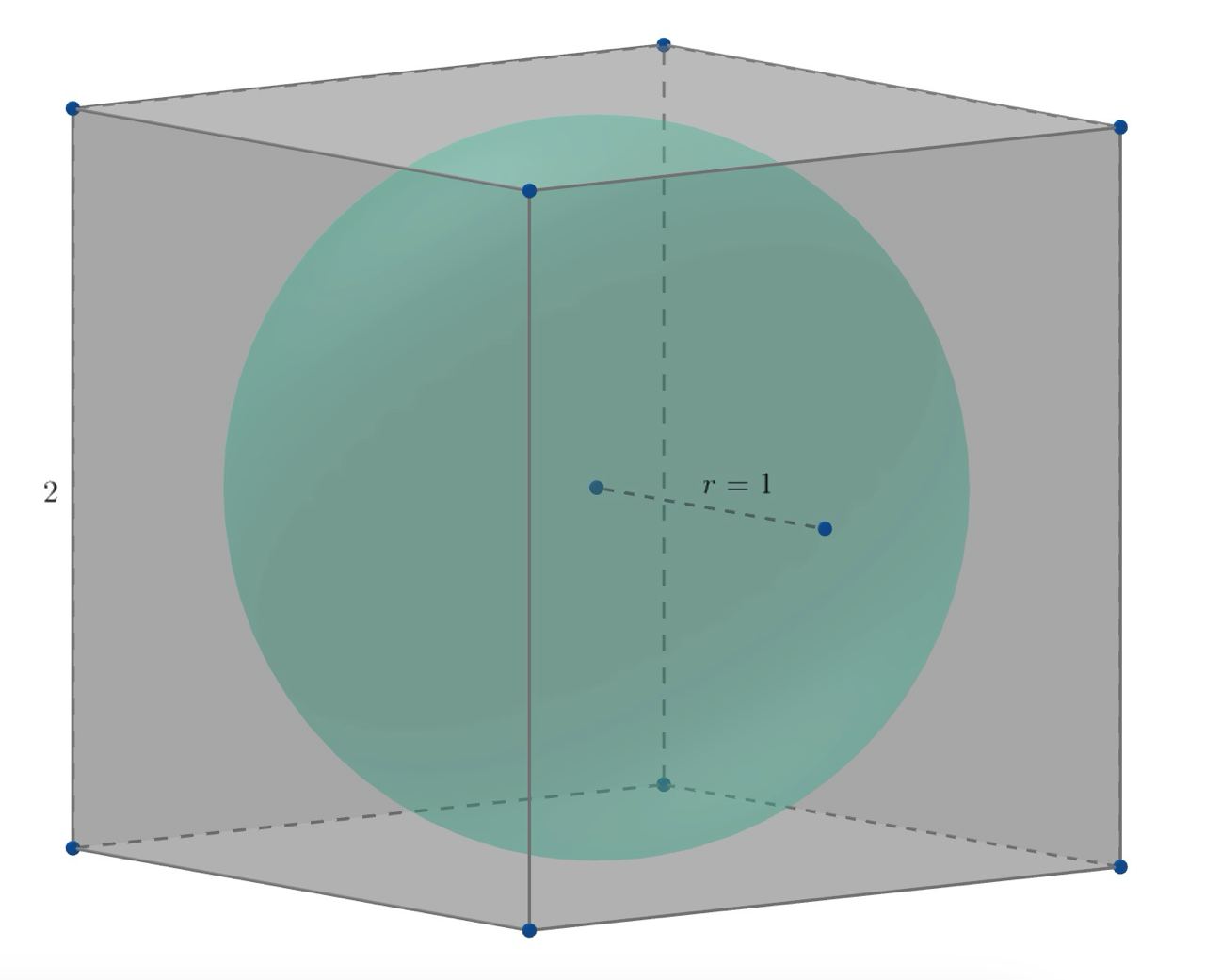
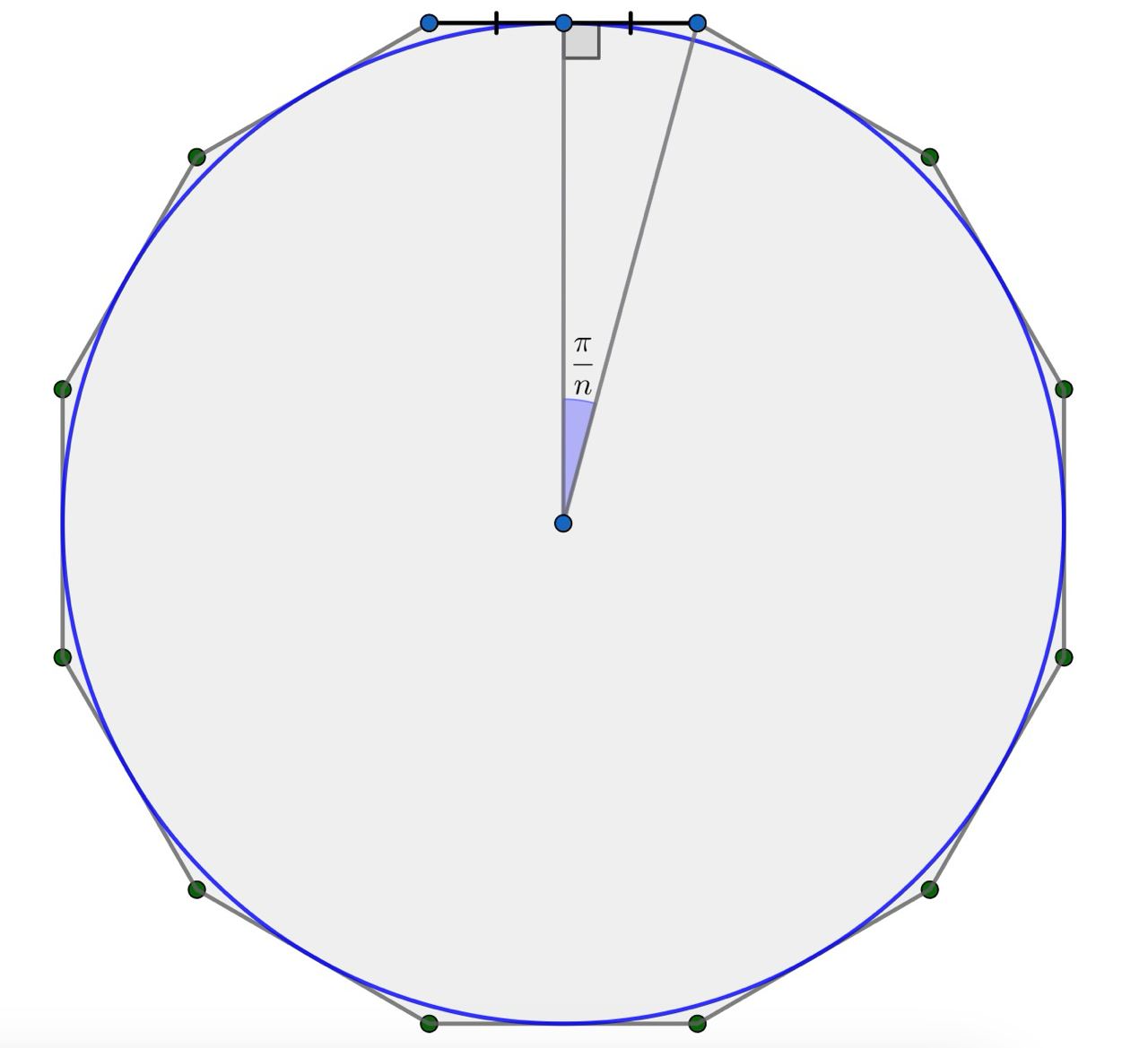
Основания призмы являются правильными $n$ -угольниками, описанными около окружностей радиуса $1.$ Согласно известной формуле, сторона основания в этом случае равна $π 2tgn.$

$PIC$

Поверхность шара, касающегося рёбер призмы, пересекает каждую из граней по окружности.

$PIC$

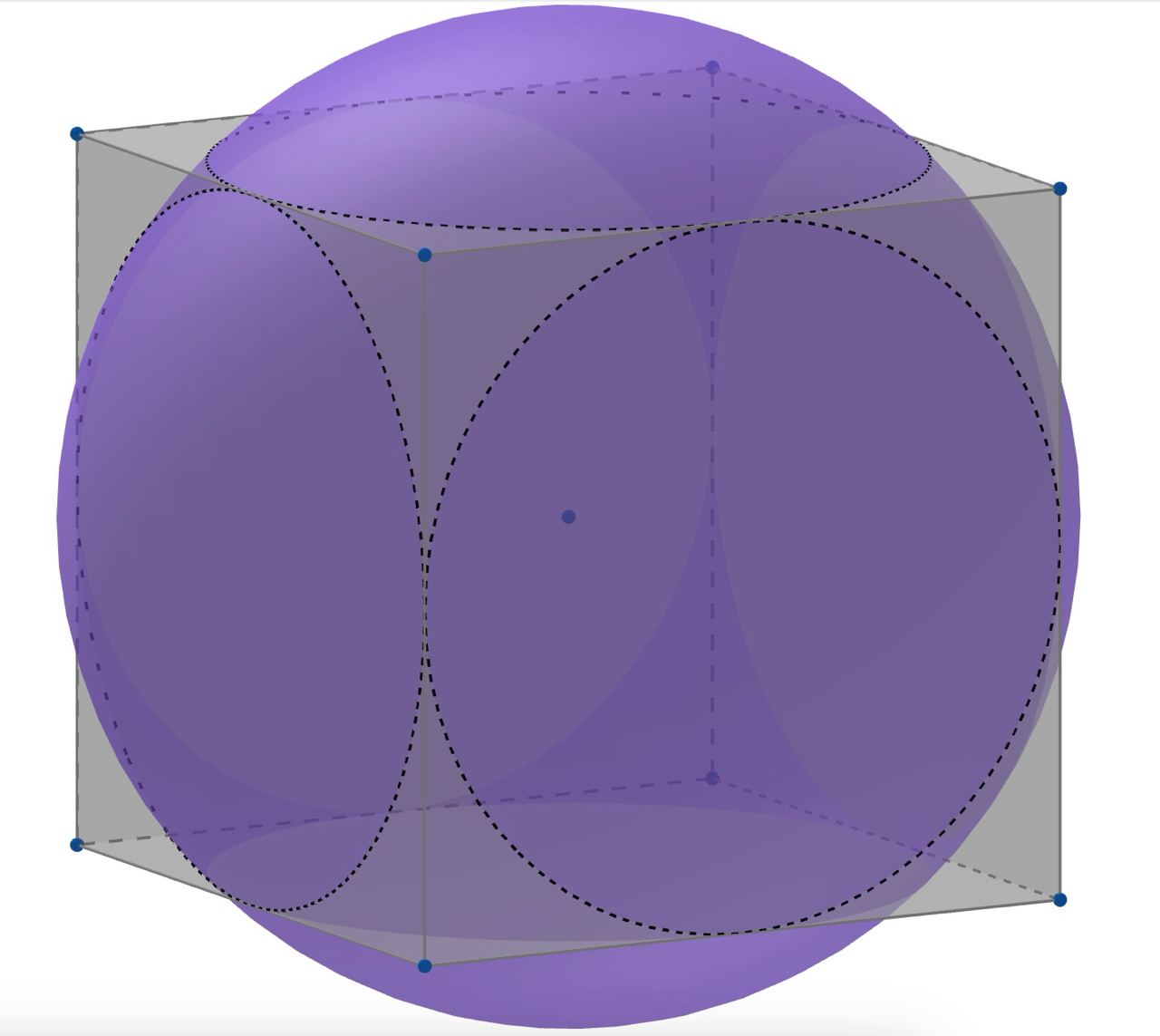
Это значит, что прямоугольники, служащие боковыми гранями, описанные, а потому являются квадратами. Отсюда $2tg πn = 2$ и $n =4.$

Таким образом, призма представляет собой куб $2× 2×2.$

Ответ:

$V = 8$

Ошибка.
Попробуйте повторить позже

Задача 33#107094Максимум баллов за задание: 7

На боковых рёбрах $TA,TB,T C$ правильной треугольной пирамиды $T ABC$ соответственно выбраны точки $A ,B ,C 1 1 1$ так, что $-TA TB- -TC TA1 = TB1 = TC1 = 3$ . Точка $O$ — центр сферы, описанной около пирамиды $TABC1.$ Докажите, что прямая $T O$ перпендикулярна плоскости $A1B1C.$ Найдите радиус этой сферы и объём пирамиды $TA1B1C,$ если сторона основания $AB = 1,$ боковое ребро $TA = 5∕4.$

Подсказки к задаче

Подсказка 1

Посмотрим на цепочку соотношений из условия, которая равна 3. Почему именно эти отношения влияют на расположение точек A₁, B₁, C₁ на рёбрах пирамиды? Возможно, стоит посмотреть на подобия каких-то треугольников.

Подсказка 2

Иногда можно использовать идею проецирования центра сферы на разные плоскости. Подумайте, почему такая проекция на боковые грани позволяет утверждать, что есть общий перпендикуляр к двум прямым, пересекающимся на плоскости из условия.

Подсказка 3

Воспользуемся теоремой о трёх перпендикулярах. К какой прямой и плоскости её стоит применить?

Подсказка 4

Применяем теорему о трёх перпендикулярах к TO и пересекающимся B₁C и A₁C в плоскости A₁B₁C и доказываем требуемое. Теперь перейдём ко второй части задачи. Для этого полезно рассмотреть высоту пирамиды и вспомнить, что в основании неё лежит равнобедренный треугольник. Подумайте, какие дополнительные точки (например, на рёбрах пирамиды) могут упростить вычисления.

Подсказка 5

Для нахождения объёма пирамиды может оказаться нужным найти её высоту, введя дополнительный угол и его синус/косинус, установить, каким отношением связаны основания A₁B₁ и AB и использовать тот факт, что T лежит на TO, которая по доказанному перпендикулярна плоскости из условия. Для нахождения радиуса вспоминаем формулу со стороной и синусом противолежащего угла!

Показать ответ и решение

1) Докажем, что прямая $TO$ перпендикулярна плоскости $A B C. 1 1$ Точка $O$ лежит в плоскости $TCD$ , $D$ — середина $AB.$ Спроецируем точку $O$ на плоскость $TBC,$ ее проекция $O1$ центр описанной около треугольника $TBC1$ окружности. Прямая $TO1$ — проекция $TO$ на плоскость $T BC.$ Докажем, что $TO1 ⊥B1C.$

$PIC$

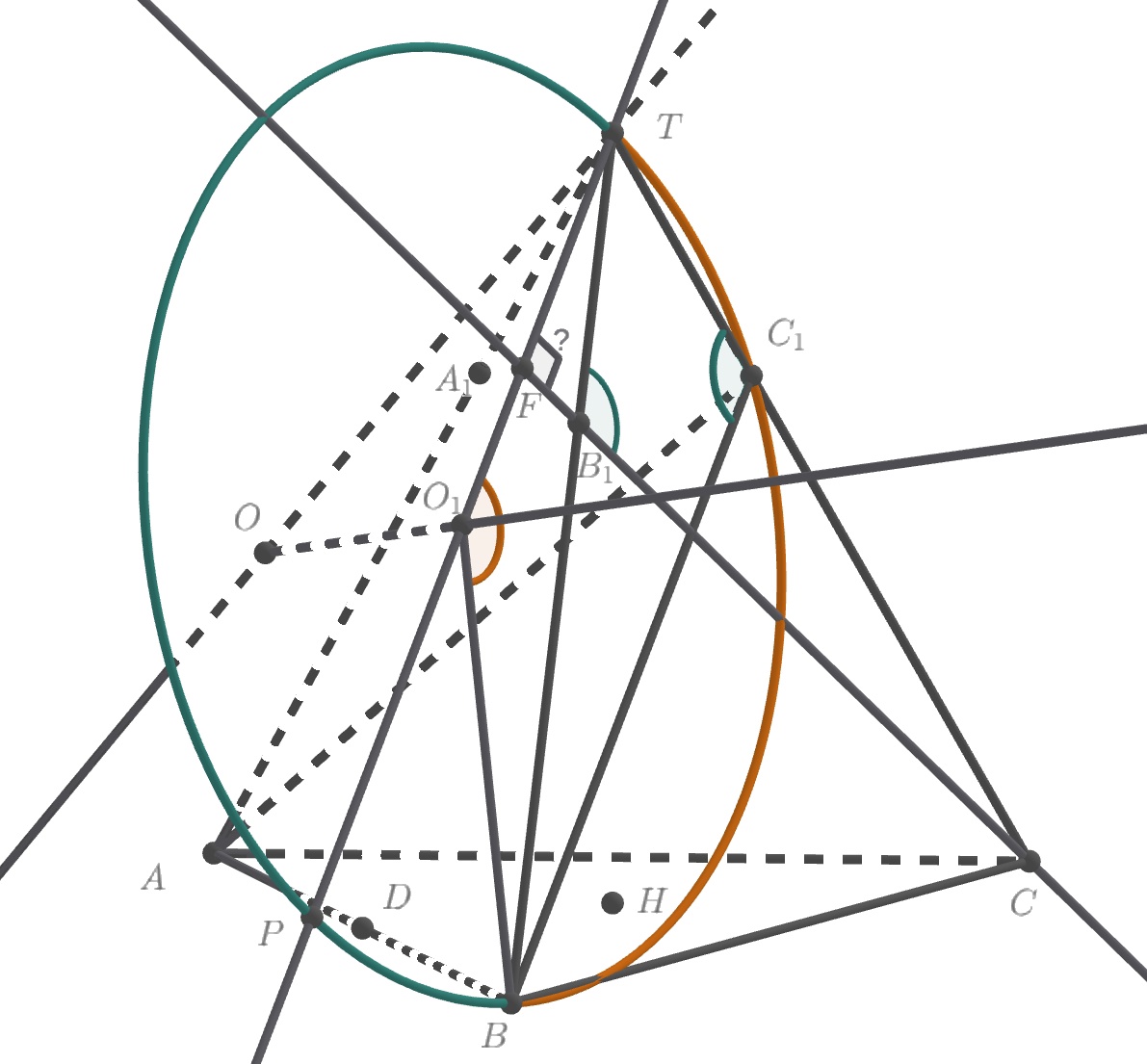
Поскольку $-TA = TB-= TC- =3, TA1 TB1 TC1$ то $△T B C 1 1$ подобен $△T BC,$ тогда $B C ∥BC, 1 1$ $∠BC T = ∠CB T. 1 1$ Докажем, что $∠CB T − ∠BTO = 90∘, 1 1$ т.е. $∠TFB = 90∘, 1$ $F$ — точка пересечения прямых $TO 1$ и $B C. 1$ По свойству вписанных углов имеем:

1 ∘ ∘ ∠BO1T- ∠CB1T = ∠BC1T = 2(360 − ∠BO1T )=180 − 2

Пусть $TP$ — диаметр рассматриваемой окружности. Тогда

1 1 ∠BO1T ∠BT O1 = ∠BT P = 2∠BO1P =2 (180∘− ∠BO1T)= 90∘−--2---

( ) ( ) ∠CB1T − ∠BTO1 = 180∘− ∠BO1T- − 90∘− ∠BO1T- =90∘ 2 2

Таким образом, $TO1 ⊥ B1C.$

Аналогично доказывается, что проекция $T O$ на плоскость $TAC$ перпендикулярна $A1C.$ Согласно теореме о трех перпендикулярах, $TO$ также будет перпендикулярна двум пересекающимся прямым $B1C$ и $A1C,$ лежащим в плоскости $A1B1C,$ следовательно, $TO ⊥ A1B1C.$

2) Обозначим через $a$ длину стороны основания пирамиды $TABC,$ $AB =a =1.$ Обозначим через $b$ длину бокового ребра пирамиды $TABC,$ $TC = b= 5∕4.$ Пусть $TH$ — высота пирамиды $T ABC.$ Тогда $TH = ∘b2-− a2∕3.$ В основании пирамиды $TA1B1C$ лежит равнобедренный треугольник $A B C, 1 1$ $A B = a∕3, 1 1$ $D C 1$ — его высота, $D 1$ — середина $A B . 1 1$ Высота $TL$ пирамиды $TA B C, 1 1$ проведенная из вершины $T$ лежит на прямой $TO.$ Для вычисления объема пирамиды $TA B C 1 1$ нужно найти $D C 1$ и $TL.$

$PIC$

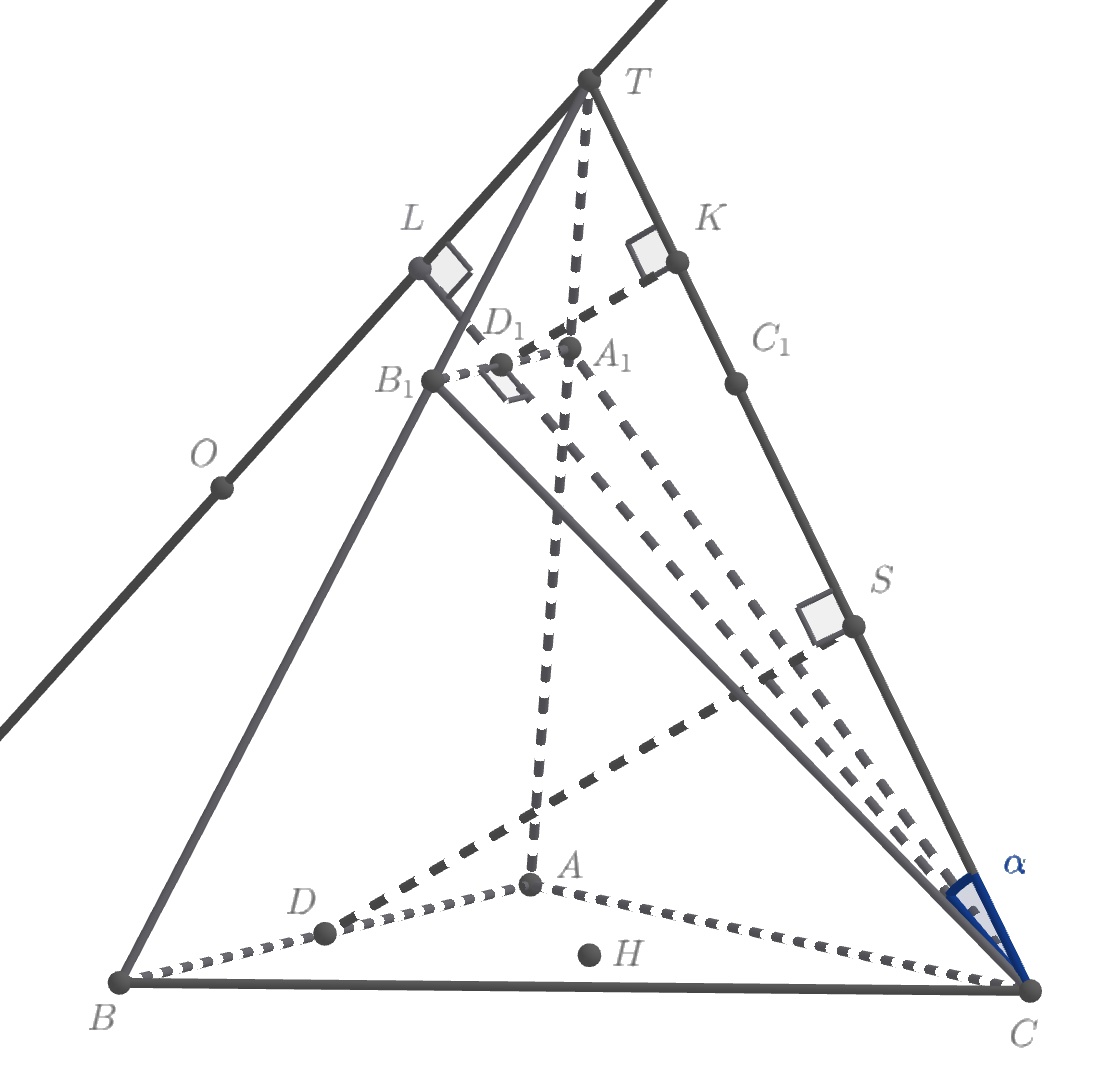
На боковом ребре $TC$ отметим точки $K$ и $S$ так, что $D1K ⊥T C,DS ⊥ TC.$

√- ∘------- √ ------ DS = DC-⋅TH-= -3a∕2⋅-b2−-a2∕3-= a-3b2−-a2- TC b 2b

a√3b2−-a2 √3a D1K = ----6b---,cos∠HCT = -3b-

√- √ - 2 KC1 = D1C1cos∠HCT = -3a--3a-= a- 6 3b 6b

KC = a2+ 2b= a2+-4b2 6b 3 6b

Пусть $∠D1CT =α.$ Тогда

√ ------ √ ------ tgα= D1K-= a--3b2−-a2, sinα = ∘-tgα---= -a√--3b2−-a2- KC a2+ 4b2 1 +tg2α b 11a2+ 16b2

Значит,

a√3b2− a2 TL =bsin α= √11a2+-16b2

√ --------- D1C =∘D1K2--+KC2-= --11a2+-16b2 6

Итак, объем пирамиды $T A1B1C$ вычисляется по формуле

1 A1B1⋅D1C- a2√3b2− a2 √59 VTA1B1C = 3 ⋅ 2 ⋅TL= 108 = 432

TC1 b2√11a2-+16b2 25 R =OT = 2sin-α =-6a√3b2−-a2--= 4√59

Ответ:

$-25- √59- R = 4√59; VTA1B1C = 432$

Ошибка.
Попробуйте повторить позже

Задача 34#33590Максимум баллов за задание: 7

Сфера с центром $O$ вписана в трёхгранный угол с вершиной $S$ и касается его граней в точках $K,L,M$ (все плоские углы трёхгранного угла различны). Найдите угол $KSO$ и площадь сечения данного трёхгранного угла плоскостью $KLM$ , если известно, что площади сечений трёхгранного угла плоскостями, касающимися сферы и перпендикулярными прямой $SO$ , равны $1$ и $4$ .

Источники: Физтех - 2020, 11.4 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Раз нас просят отыскать ∠KSO будет рассматривать плоскость (KSO), а, точнее, ту её часть, что заключена между прямыми SO и SK. Нам понадобятся точки P и Q — точки касания сферы с плоскостями, перпендикулярными SO. Пусть при это SP < SQ. Отметьте всё, что можно выразить через радиус сферы.

Подсказка 2

Рассмотрим отрезки, заключенные между точками пересечения SK и SO с касательными к сфере плоскостями. Если мы знаем отношение площадей сечений, то что можно сказать об отношении этих отрезков? (Вспомните: площади подобных треугольников относятся как квадрат коэффициента подобия). Пользуясь этим отношением вы сможете найти связь между SP и радиусом сферы.

Подсказка 3

Помните: радиус сферы, проведённый в точку касания, перпендикулярен касательной плоскости. А значит, мы можем найти синус ∠KSO, ведь всё нужное для этого мы выразили через радиус сферы.

Подсказка 4

Что можно сказать про (KLM) и SO? Проведите высоты к SO в △KSO, △MSO и △LSO — это поможет нам сделать важный вывод!

Подсказка 5

После того, как мы заметили перпендикулярность (KLM) и SO, можно поработать с подобными прямоугольными треугольниками: узнав отношение отрезков параллельных секущих плоскостей, заключённых между точками их пересечения с SO и SK, мы сможем сделать вывод и об отношениях площадей сечения!

Показать ответ и решение

Обозначим точки пересечения прямой $SO$ со сферой через $P$ и $Q$ (точка $P$ лежит на отрезке $SO$ , а $Q$ — вне него). Пусть радиус сферы равен $r$ . Треугольники $OKS, OLS$ и $OMS$ прямоугольные (углы при вершинах $K, L,M$ прямые, так как касательные перпендикулярны радиусам, проведённым в точку касания). Эти треугольники равны по катету и гипотенузе $(OK =OL = OM = R,SO$ — общая), следовательно, $∠KSO = ∠LSO = ∠MSO ($ пусть $∠KSO = α,SO= x)$ . Высоты, опущенные из точек $K,L,M$ на гипотенузу $SO$ , paвны, а их основания — одна и та же точка $H$ , лежащая в плоскости $KLM$ (назовём эту плоскость $τ)$ . Пусть $β$ и $γ$ касательные плоскости к сфере, проходящие через точки $P$ и $Q$ , а $E$ и $F$ — точки пересечения этих плоскостей с прямой $SK$ . По условию площади сечений трёхгранного угла этими плоскостями равны соответственно $S1 =1$ и $S2 =4$ . Рассмотрим сечение трехгранного угла и сферы плоскостью $SKO$ (см. рис. и обозначения на нем). Так как $SH ⊥HK$ и $SH ⊥ HL$ , то $τ ⊥ SH$ . Тогда сечения трёхгранного угла плоскостями $τ,β$ и $γ$ — подобные треугольники, плоскости которых параллельны (все они перпендикулярны $SO )$ .

Если $Σ$ — площадь треугольника, получающегося в сечении трёхгранного угла плоскостью $KLM$ , то из подобия $Σ :S1 :S2 = KH2 :EP2 :FQ2.$ Следовательно, $√-- √-- EP :FQ = S1 : S2.$ Тогда $√ -- √-- S1 : S2 = SP :SQ= (x− r) :(x+ r),$ откуда $√-- √-- r= x√SS22−+√SS11,$ a $√-- √-- sinα = rx = √SS22−+√SS11 = 13.$ Отсюда $∠KSO =arcsin13.$

$PIC$

Далее, $OH = rsinα,SH = SO− OH = -r- − rsin α,SP = SO− r=-r- − r. sinα sinα$ Значит, $Σ :S1 = KH2 :EP2 =SH2 :SP2 = (-1 − sin α)2 :(-1 − 1)2 = (1+sinα)2 = 16, sinα sinα 9$ откуда $Σ= 16. 9$

Ответ:

$∠KSO =arcsin1,S = 16 3 9$

Ошибка.
Попробуйте повторить позже

Задача 35#100421Максимум баллов за задание: 7

(a) Сфера с центром $O$ касается боковых рёбер $SA,SB,SC$ пирамиды $SABC$ в точках $K,L,M$ соответственно, а также касается её основания $ABC.$ Через точку сферы, ближайшую к точке $S,$ проведена плоскость, касающаяся сферы. Площадь сечения пирамиды $SABC$ этой плоскостью равна 9, а $√35- ∠KSO = arccos 6$ . Найдите площадь треугольника $KLM.$

(b) Пусть дополнительно известно, что $SO = 25,$ а плоскости $KLM$ и $ABC$ параллельны. Найдите объём пирамиды $SABC.$

Источники: Физтех - 2020, 11.4 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Давайте заметим, что плоскость KLM и плоскость, каcающаяся сферы в точке, ближайшей к S, параллельны (надо бы это доказать).

Подсказка 2

Учитывая, что площадь одного сечения известна, площадь второго можно найти через подобие. Вот бы коэффициент подобия узнать...

Подсказка 3:

Давайте обозначим через P и Q точки пересечения SO с окружностью, а через A₁ — точку пересечения перпендикуляра к SO в Q и SA. Для вычисления коэффициента подобия осталось лишь проделать небольшие махинации с треугольником SA₁Q.

Подсказка 4:

Во втором пункте стоит подумать про точки A и A₁, учитывая дополнительное условие. Что можно сказать про их взаимное расположение?

Показать ответ и решение

а) Пусть радиус сферы равен $R$ . Обозначим точки пересечения прямой $SO$ со сферой через $P$ и $Q$ (точка $P$ лежит на отрезке $SO$ , а $Q$ — вне него). Треугольники $OKS,OLS$ и $OMS$ прямоугольные (углы при вершинах $K,L,M$ прямые, так как касательные перпендикулярны радиусам, проведённым в точку касания). Эти треугольники равны по катету и гипотенузе $(OK =OL = OM = R,SO$ — общая), следовательно, $∠KSO = ∠LSO = ∠MSO$ (обозначим эти углы через $1 α;sinα = 6$ ); высоты, опущенные из точек $K,L,M$ на гипотенузу $SO$ , равны, а их основания — одна и та же точка $H$ , лежащая в плоскости $KLM$ (назовём эту плоскость $τ)$ . Пусть $σ$ — касательная плоскость к сфере, проведённая через точку $P$ . Обозначим точку пересечения $σ$ и $SA$ через $E$ . Рассмотрим сечение пирамиды и сферы плоскостью $ASO$

$PIC$

Из прямоугольного треугольника $KSO$ получаем $SO = siRnα$ . Тогда

( ) SP = SO − OP = R-1--− 1 sinα

Пусть площадь сечения пирамиды плоскостью $σ$ равна $S0 =9$ , а плоскостью $τ − SKLM$ . Из подобия следует, что

2 2 2 2 SKLM :S0 = (KH :EP )= (SH :SP) = (SO − OH) :SP =

( R )2 2( 1 )2 2 = sinα-− Rsinα :R sinα − 1 = (1+sin α)

Следовательно,

SKLM = S0(1 +sin α)2 = 12,25

б) Если плоскости $τ$ и $ABC$ параллельны, то точка $A$ совпадает с точкой $A1$ такой, что $A1Q ⊥$ $SO :$

$PIC$

Тогда, обозначив площадь треугольника $ABC$ через $SABC$ , получаем

1 1 ( SQ)2 VSABC = 3 ⋅SQ ⋅SABC = 3 ⋅(SO +R)⋅S0⋅ SP =

= 13 ⋅(SO+ SOsinα)⋅S0⋅(SO +SO sinα)2 :(SO − SO sinα)2 =

3 = 1 ⋅SO ⋅S0⋅ (1+-sinα)2 = 343 3 (1− sinα) 2

Ответ:

(a) $12,25$

(b) $171,5$

Ошибка.
Попробуйте повторить позже

Задача 36#102469Максимум баллов за задание: 7

Про тетраэдр $PQRS$ известно, что

∘ ∘ PQ =4,SR =6,∠QRS = ∠PSR = 50 ,∠QSR = ∠PRS =40 .

Вокруг тетраэдра описана сфера. Рассмотрим на этой сфере множество всех точек, сумма сферических расстояний от которых до точек $P,Q,R,S$ не меньше $6π$ . Чему равна площадь этого множества?

Замечание. Сферическое расстояние между двумя точками на сфере — длина наименьшей дуги окружности большого круга, соединяющей эти точки.

Источники: ОММО - 2020, номер 8 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте обратим внимание на треугольники PRS и QRS. Они же прямоугольные. А что можно сказать про середину гипотенузы RS и про сферу?

Подсказка 2

Давайте обратим внимание на сумму сферических расстояний от точки R до некоторой точки M и от точки M до S. Кажется, в прошлом пункте мы поняли, что RS — диаметр сферы (если не поняли, срочно вернитесь к прошлой подсказке и поймите). На каких окружностях круга лежат пары точек M, R и S, R? Они различные?

Подсказка 3

Итак, осталось показать, что сумма сферических расстояний M, P и M, Q не меньше 3π. Давайте сделаем следующий трюк. Рассмотрим точку Q₁, симметричную Q относительно центра сферы. Как можно её использовать?

Подсказка 4:

По рассуждениям из предыдущих подсказок сумма сферических расстояний Q, M и M, Q₁ равна 3π. Значит, нужно доказать, что расстояние точек M, P не меньше расстояния точек M, Q₁. Осталось немного подумать и добить задачу.

Показать ответ и решение

$PIC$

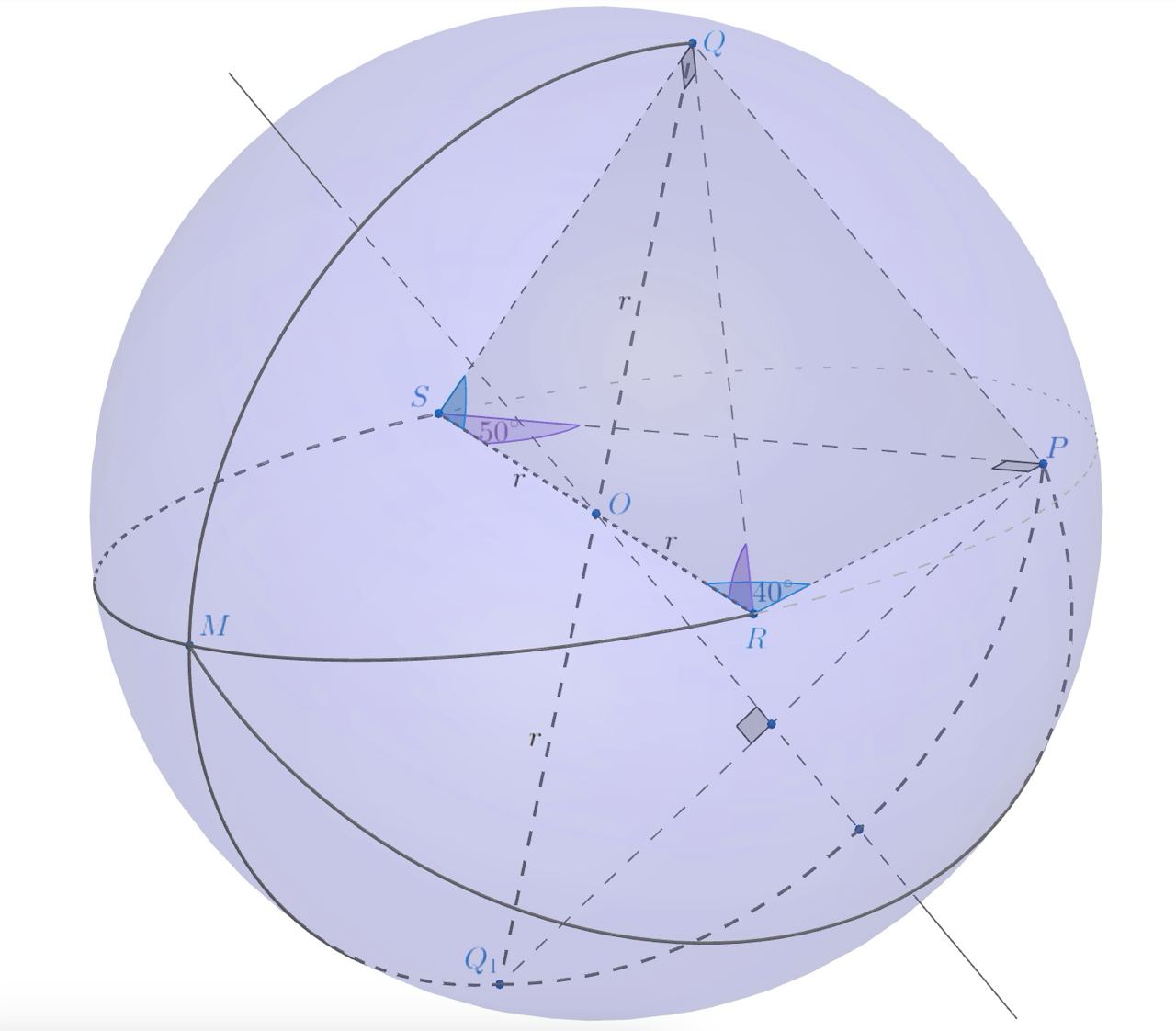
Так как

∠QRS +∠QSR = ∠PRS + ∠PSR =90∘,

то треугольники $QRS$ и $PRS$ — прямоугольные с общей гипотенузой $RS$ . Если $O$ — середина отрезка $RS$ , то по свойству медианы прямоугольного треугольника $OP = OQ = OR =OS = 3$ . Следовательно, радиус описанной сферы равен 3, а точка $O$ — её центр.

Обозначим через $d(X,Y )$ сферическое расстояние между точками $X$ и $Y$ . По условию задачи необходимо найти площадь множества $ω$ на сфере, состоящего в точности из точек $M$ , для которых

d(M,P )+d(M,Q)+ d(M, R)+ d(M,S) ≥6π (1)

Поскольку $RS$ — диаметр сферы, то точки $R,M$ и $S$ лежат на одной окружности большого круга; следовательно,

d(R,M)+ d(M, S)= d(R,S)= 3π

Неравенство (1) перепишется в виде

d(M, P)+ d(M,Q )≥3π

Пусть $Q1$ — точка, симметричная точке $Q$ относительно центра сферы $O$ . Так как $Q1$ и $Q$ — концы диаметра сферы, то

d(Q,M )+ d(M, Q )= d(Q,Q ) =3π 1 1

Подставляя $d(M, Q)= 3π− d (M, Q1)$ в неравенство (2), получаем

d(M,P)≥ d(M,Q1)

Так как $PQ = 4⁄= 6$ , то $PQ$ не является диаметром, а потому $Q1 ⁄= P$ . Итак, $ω$ есть множество точек на сфере, сферическое расстояние от которых до одной точки на сфере не превосходит сферического расстояни до другой точки на сфере. В силу симметрии (относительно плоскости, проходящей через центр сферы перпендикулярно отрезку $Q1P$ , $ω$ — половина сферы и её площадь равна

1 ⋅4 ⋅π ⋅32 =18π 2

Ответ:

$18π$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 37#103217Максимум баллов за задание: 7

Две правильные треугольные пирамиды имеют общую боковую грань и не имеют других общих точек. В пирамиды вписаны шары радиуса $r.$ Третий шар радиуса $R$ касается внешним образом обеих пирамид и вписанных в них шаров. Найдите плоский угол при вершине пирамид, если $R :r= 2:1.$

Источники: СПБГУ - 2020, 11.6 (см. olympiada.spbu.ru)

Подсказки к задаче

Подсказка 1

Пусть O₁ и O₂ - центры вписанных сфер, а O — центр внешней сферы. Рассмотрите треугольник OO₁O₂, из него можно получить много информации.

Подсказка 2

Ну, во-первых, он равнобедренный. Во-вторых, вы можете выразить его стороны через радиусы. В-третьих, попробуйте рассмотреть точки K — середину O₁O₂, M — точка касания сферы и одной из пирамид и точку N касания вписанных сфер. Что можно сказать про угол MNK и чему он равен?

Подсказка 3

Это угол между боковыми гранями пирамиды. Кстати, почему? Пусть боковое ребро пирамиды равно a. Используя величину угла, вы сможете выразить длину ребра основания через a, если проведёте высоты в двух боковых гранях к одному ребру. А там и до плоского угла при вершине недалеко.

Показать ответ и решение

Пусть $SABC$ — первая пирамида, $BSC$ — её общая боковая грань со второй, $O 1$ и $O 2$ — центры шаров, вписанных в пирамиды, $O$ — центр внешнего шара. Ввиду равенства пирамид вписанные в них шары касаются грани $BSC$ в одной точке $K.$ Так как $O1K ⊥BSC$ и $O2K ⊥ BSC,$ точка $K$ лежит на отрезке $O1O2,$ причём $O1O2 = 2r.$

Пусть $M$ — точка касания с гранью $ASB$ шара, вписанного в первую пирамиду. В этой же точке касается $ASB$ и внешний шар. Поэтому точка $M$ лежит на отрезке $OO1,$ причём $OO1 =r +R.$ Аналогично получается, что $OO2 = r+R.$ Выберем точку $N$ на отрезке $OK$ так, что $NM ⊥ OO1,$ и положим $φ= ∠MNK.$

$PIC$

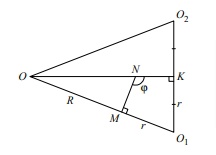
Тогда

( ) O1K = OO1 ⋅cos∠OO1K ⇐⇒ r=(r+ R)⋅cos(π− φ)⇐⇒ R = −r --1-+ 1 . cosφ

По условию $R =2r,$ откуда $1 cosφ =− 3.$

Покажем, что $φ$ — угол между гранями $ASB$ и $BSC.$ Действительно, $O1K$ и $O1M$ — радиусы шара, вписанного в первую пирамиду, откуда $O1M ⊥ ASB$ и $O1K ⊥ BSC.$ Значит, $BS ⊥MNK.$ Кроме того, прямая $MN$ лежит в плоскости $ASB$ , а $KN$ — в плоскости $BSC.$

$PIC$

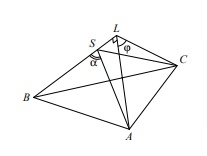
Пусть $α= ∠ASB,a= AB.$ Опустим из точек $A$ и $C$ перпендикуляры на ребро $BS.$ Они придут в одну точку $L,$ так как треугольники $ASB$ и $BSC$ равны. По доказанному $∠ALC = φ.$ Заметим, что

AL2 =(AB ⋅sin∠ABL )2 = a2sin2(π − α)= a2cos2 α-= a2(1-+cosα). 2 2 2 2

Тогда по теореме косинусов для треугольника $ALC$

2 2 2 2 − 1= cosφ =2AL--− AC-= a-(1-+cosα)− a = 3 2AL2 a2(1+ cosα ) ( ) = -cosα--⇐ ⇒ cosα = − 1 =⇒ α= arccos − 1 =π − arccos1. 1+cosα 4 4 4

Ответ:

$π − arccos1 4$

Ошибка.
Попробуйте повторить позже

Задача 38#123417Максимум баллов за задание: 7

На сфере радиуса $1$ дан треугольник, стороны которого — дуги трёх различных окружностей радиуса $1$ с центром в центре сферы, имеющие длины меньше $π,$ а площадь равна четверти площади сферы. Докажите, что четырьмя копиями такого треугольника можно покрыть всю сферу.

Источники: Тургор - 2020, 11.5, устный тур (см. turgor.ru)

Подсказки к задаче

Подсказка 1

Используя формулу площади сферического треугольника, можно вычислить сумму его углов.

Подсказка 2

Попробуйте угадать на сфере такую точку D, чтобы треугольники CDA, DCB и DAB были равны треугольнику ABC.

Подсказка 3

Чтобы было проще найти такую точку, попробуйте сначала найти такую, чтобы были равны треугольники ABC и BAD. Потом подумайте про другие.

Показать доказательство

Первое решение.

Пусть $O$ — центр сферы, а $ABC$ — данный сферический треугольник. По формуле площади сферического треугольника

π = SABC =∠A + ∠B+ ∠C − π

то есть $∠A + ∠B+ ∠C =2π.$ (Доказательство формулы площади заключается в применении формулы включений-исключений к трём полусферам, пересечением которых является данный треугольник.)

$PIC$

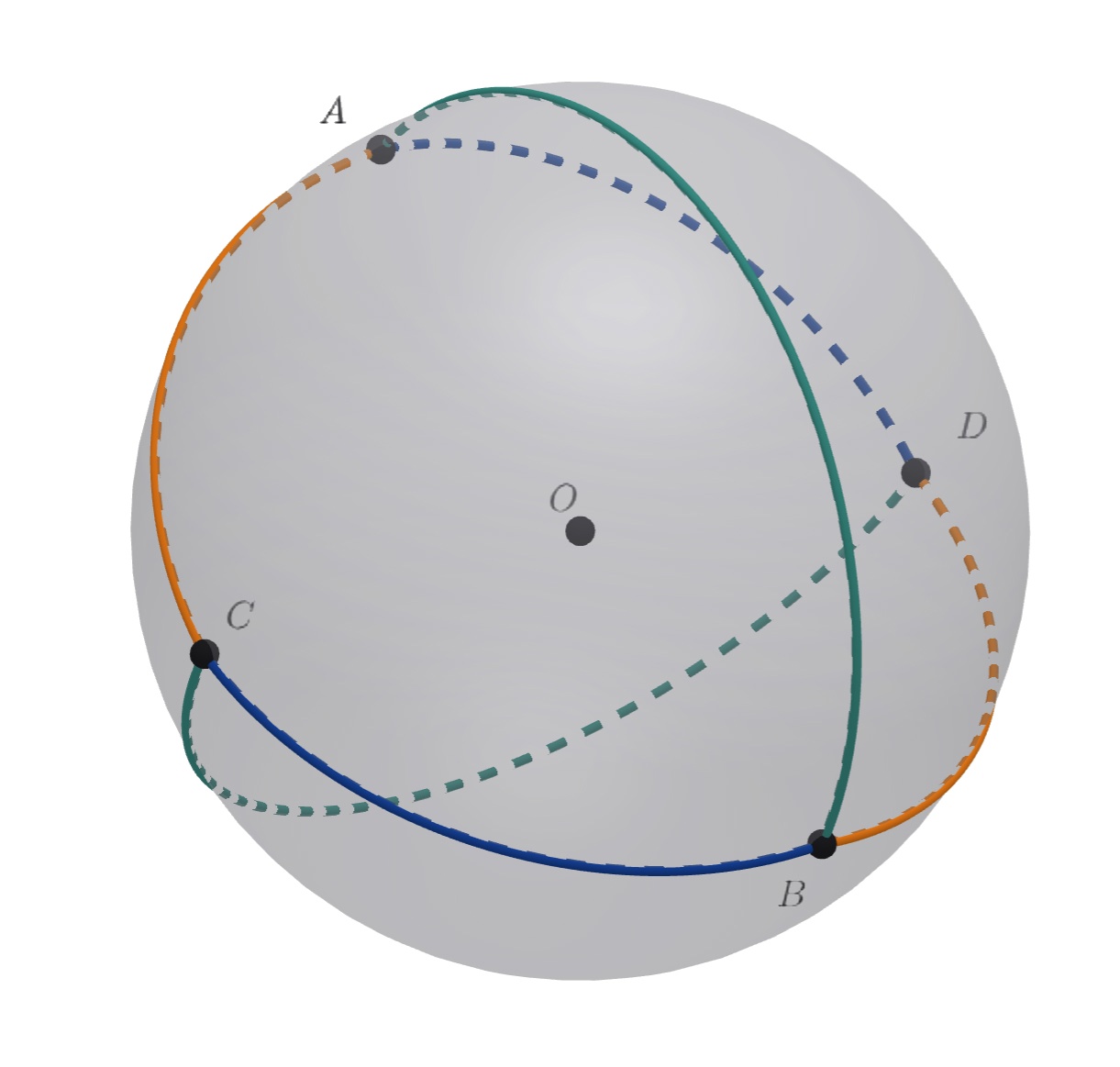
Построим на сфере точку $D,$ лежащую с $C$ в разных полуплоскостях относительно $OAB,$ и такую, что $∠DAB = ∠CBA$ и $∠DBA =∠CAB$ (имеются в виду сферические углы; иначе говоря, точка $D$ получена из $C$ композицией симметрии относительно $OAB$ и симметрии относительно серединного перпендикуляра к $AB ).$ Тогда треугольники $ABC$ и $BAD$ равны. Значит, $BD = AC$ и $AD = BC.$ Но из условия имеем $∠DAC = ∠DBC = ∠ACB,$ следовательно, сферические треугольники $CDA$ и $DCB$ также равны треугольнику $ABC.$ Четыре полученных треугольника покрывают сферу, так как в сумме без пересечений покрывают поверхность $4π,$ равную площади поверхности всей сферы.

Второе решение.

$PIC$

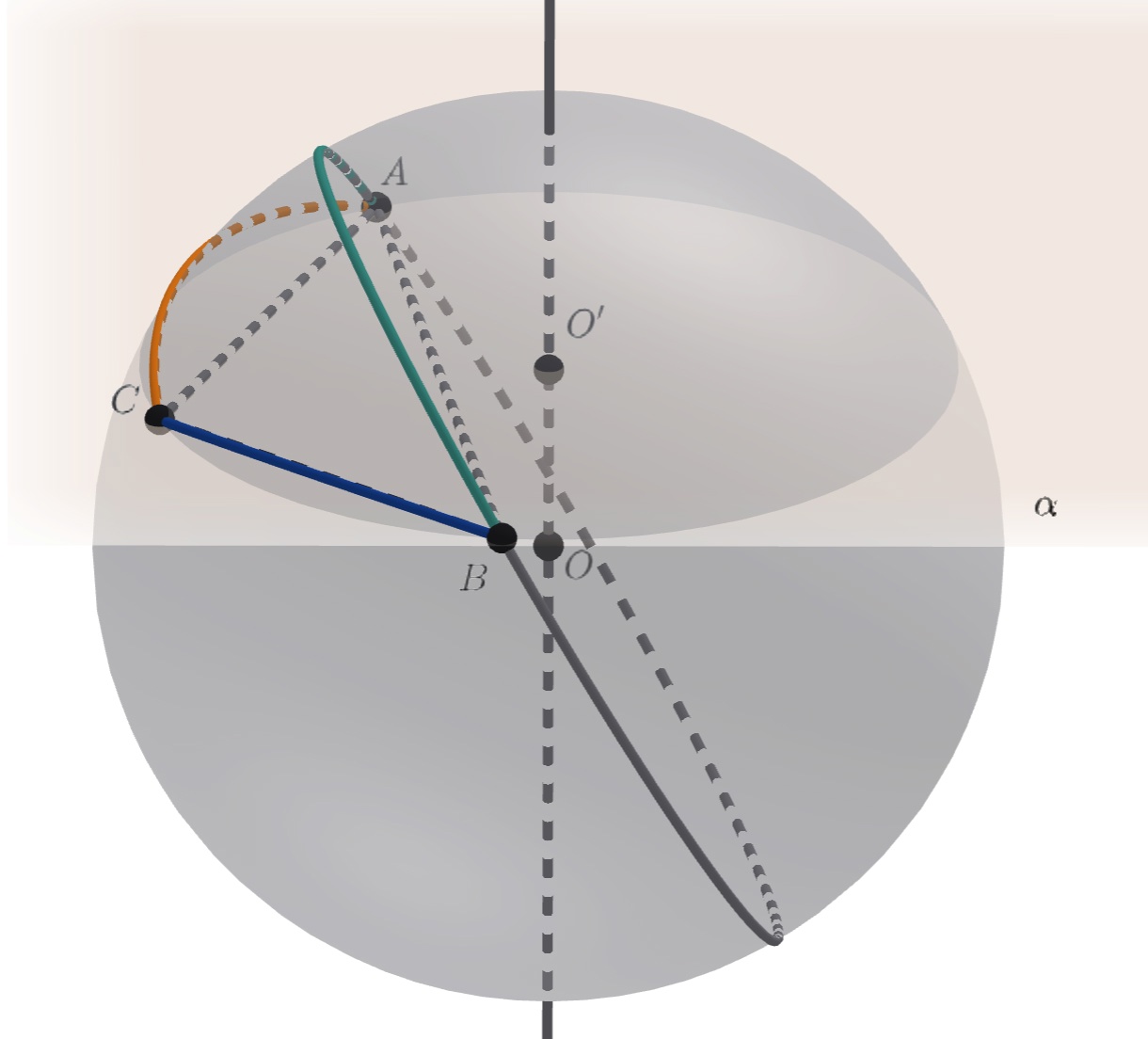
Пусть $A,B,C$ — вершины данного треугольника. Покажем, что треугольник $ABC$ остроугольный. Действительно, пусть $∠ACB ≥π∕2.$ Если плоскость $α= ABC$ содержит центр $O$ сферы, то сферический треугольник $ABC$ вырожден, и его площадь не такая, как надо. Иначе $α$ отрезает от сферы «шапочку» площади меньше полусферы. Далее, прямая $AB$ (нестрого) разделяет $C$ и проекцию $O$ на $ABC;$ значит, часть шапочки, отсекаемая плоскостью $OAB$ и содержащая $C,$ не больше её половины. Наконец, сферический треугольник $ABC$ лежит в этой области, площадь которой меньше четверти площади сферы — противоречие.

$PIC$

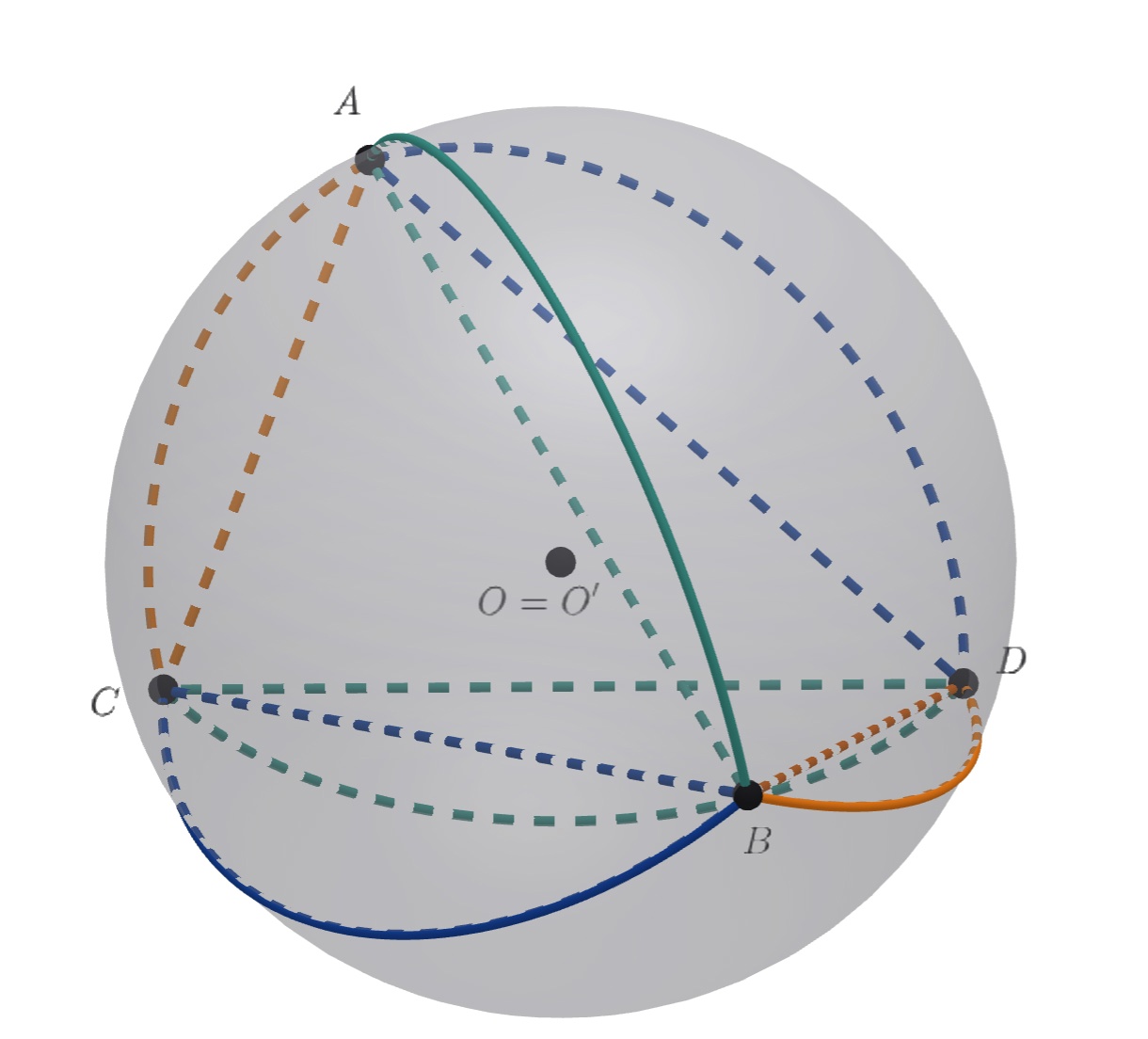
Итак, треугольник $ABC$ остроугольный; тогда существует равногранный тетраэдр $ABCD$ (точки $D$ и $O$ лежат в одной полуплоскости относительно $ABC).$ Пусть $O′$ — центр этого равногранного тетраэдра. Тогда телесные углы $O ′ABC, O′BCD, O ′CDA, O′DAB$ разбивают пространство, то есть каждый из них равен четверти площади единичной сферы. Однако, если $O ′$ ближе к $ABC,$ чем $O,$ то этот телесный угол больше, чем $OABC,$ а если $O ′$ дальше, то меньше. Оба случая невозможны; значит, $O = O′,$ и упомянутые телесные углы дают требуемое разбиение сферы на 4 части.

Ошибка.
Попробуйте повторить позже

Задача 39#43959Максимум баллов за задание: 7

Дана усечённая пирамида $ABCA B C 1 1 1$ с боковыми рёбрами $AA 1$ , $BB 1$ , $CC 1$ $(ABC ∥A B C ) 1 1 1$ , такая, что треугольник $BB1C$ — равносторонний. На ребре $AA1$ , перпендикулярном основанию $ABC$ пирамиды, лежит точка $N$ такая, что $AN :NA1 = 1:2.$ Сфера $Ω$ с радиусом $√- 5$ проходит через вершины треугольника $BB1C$ и касается отрезка $AA1$ в точке $N$ .

(a) Найдите длину ребра $BB1$ .

(b) Пусть дополнительно известно, что $∘ -- ∠ABC =arccos 25$ . Найдите угол между прямой $AA1$ и плоскостью $BB1C$ , а также длину ребра $A1B1.$

Подсказки к задаче

Пункт а), подсказка 1

Введем обозначения: пусть E – вершина пирамиды, O – центр сферы ω, O₁ – центр описанной окружности треугольника BB₁C, а F – середина BC. Если треугольник BB₁C равносторонний, то чем еще будет являться точка O₁? А какие прямые будут проходить через нее?

Пункт а), подсказка 2

Верно, O₁ будет также точкой пересечения медиан, значит через нее пройдет прямая B₁F, Вы даже можете спокойно найти, в каком отношении точка O₁ поделит отрезок B₁F. А что тогда можно будет сказать про взаимное расположение прямой NO₁ и плоскости (ABC)?

Пункт а), подсказка 3

Конечно, прямая NO₁ будет параллельна плоскости (ABC). А теперь поработаем с нашей сферой! Из условия сфера касается AA₁ в точке N, а также проходит через вершины треугольника BB₁C, чему тогда будут перпендикулярны прямые OO₁ и ON?

Пункт а), подсказка 4

OO₁ ⊥ (BB₁C), ON ⊥ AA₁, а еще по условию AA₁ ⊥ (ABC), тогда ON будет параллельна плоскости (ABC)! Остается понять, что точка O₁ совпадает с точкой O. Для этого рассмотрите плоскость α, которая будет проходить через точку N параллельно плоскости (ABC), а также рассмотрите прямую l, которая перпендикулярна (BB₁C) и проходит через точку O₁. Что будет, если прямая l будет лежать в плоскости α?

Пункт а), подсказка 5

Действительно, такой ситуации быть не может, ведь тогда FB₁ ⊥ l, FB₁ ⊥ BC, а это две разные прямые, которые параллельны (ABC), тогда получается, что (BB₁C) ⊥ (ABC), а такого не может быть в нашей пирамиде! Тогда делаем вывод, что l пересекает α в одной точке, поэтому O₁ = O, что и хотелось показать. Теперь вовсе не составит труда найти сторону равностороннего треугольника BB₁C, если известно, что радиус его описанной окружности совпадает с радиусом сферы.

Пункт б), подсказка 1

Пусть O' – проекция O на (ABC), а B₁' – проекция B₁ на (ABC). Какой прямой в плоскости (ABC) будет принадлежать точка B₁'?

Пункт б), подсказка 2

Конечно, B₁' ∈ AB, можем даже узнать, в каком отношении точка O' будет делить отрезок FB₁' (покажите, что оно будет равно FO : OB₁). Тогда теперь можно будет найти длину отрезка B₁'F, нужно всего лишь показать, что треугольник BB₁'C равнобедренный, доказав равенство треугольников B₁B₁'B и B₁B₁'C. И нужный угол легко найдется, если рассмотреть угол между B₁B₁' || A₁A и нужной плоскостью.

Пункт б), подсказка 3

Пусть T – проекция O' на AB. Легко понять, что A₁B₁ = AB₁', тогда задача поиска A₁B₁ сведется к тому, что нужно будет найти AB₁' = AT + TB₁'. Найдите длину O’T, поработав с треугольником BB₁'C, а зная O’T, можно будет легко найти AT и TB₁', используя теорему Пифагора, а также факт, что AO' = ON.

Показать ответ и решение

$PIC$

Отметим точку $E$ в качестве вершины пирамиды, точку $O$ в качестве центра $ω$ , точку $O1$ в качестве центра описанной окружности треугольника $BB1C$ и $F$ в качестве середины $BC$ . Так как $BB1C$ равносторонний, то $O1$ это еще и центр пересечения медиан, а значит, $B1F$ проходит через $O1$ и $FO1 :O1B1 = 1:2$ и $NO1∥ABC$ . Так как $ω$ проходит через вершины треугольника $BB1C$ и касается отрезка $AA1$ в точке $N$ , то $OO1⊥BCC1$ и $ON ⊥AA1$ . Мы знаем, что $AA1 ⊥ABC$ и поэтому $NO ∥ABC$ . Получается, что мы знаем, что точка $O$ лежит на плоскости $α$ , проходящей через $N$ и параллельной $ABC$ , и лежит на прямой $l$ , перпендикулярной $BB1C$ и проходящей через $O1$ . Значит, либо $l$ принадлежит $α$ , но тогда $FB1$ перпендикулярна двум разным прямым параллельным $ABC$ ( $BC$ и $l$ ) и тогда все три стороны перпендикулярны основанию, а такого не бывает, либо $l$ и $α$ пересекаются в одной точке и $O1 =O$ . Тогда $BO =BO1 = √5$ и $BB1 = √15$ (по формуле для равностороннего треугольника).

$PIC$

Спроецируем точки $O$ и $B1$ на плоскость $ABC$ . Тогда так как проекция $A1$ на $ABC$ это $A$ , то $′ A1B1∥AB 1$ и поэтому $′ B ∈ AB$ . Также можно заметить $′ ′ ′ F O:OB1 = FO :O B1 = 1:2$ .

Прямоугольные треугольники $B1B′1B$ и $B1B′1C$ равны по катету и гипотенузе, поэтому $BB′1 =CB ′1$ . Значит, высота в равнобедренном треугольнике $BB ′1C$ равна $B ′1F$ , так как $F$ середина $BC$ и равна $√--∘-- ∘-- BF |tgB ′1BF |= -125 32 = 458$ . Тогда

∘-- ′ ′ (B′1F-) -458- 1-- ∠(AA1,BCB1)= ∠(B1B1,BCB1 )= ∠B1B1F =arcsin B1F = arcsin √45 = √2 2

Значит, $∠(AA1,BCB1 )= π4$ . Тогда $∘ -- FB ′1 = F√B21= 485$

Пусть $T$ — проекция $O′$ на $AB$ . Тогда $O′T = O′B′cosB ′O ′T = 2B′Fcos1∠B ′O′C = 2B′FcosB ′BC = 2∘ 45∘-2= 1 1 1 3 1 2 1 3 1 1 3 8 5$ и $∘----------- ∘ 3- B1′T = O′B′12− O ′T2 = 2$ . С другой стороны, поскольку $√- AO ′= NO = 5$ , то $√---------- AT = AO ′2− O′T2 = 1$ . Отсюда $∘ -- A1B1 =AB ′1 = AT +TB ′1 = 2+ 32$ .

Ответ:

$(a)√15,$

$π ∘-3 (b)4,2+ 2$

Ошибка.
Попробуйте повторить позже

Задача 40#90887Максимум баллов за задание: 7

Тетраэдр $ABCD$ с остроугольными гранями вписан в сферу с центром $O.$ Прямая, проходящая через точку $O$ перпендикулярно плоскости $ABC$ , пересекает сферу в точке $E$ такой, что $D$ и $E$ лежат по разные стороны относительно плоскости $ABC.$ Прямая $DE$ пересекает плоскость $ABC$ в точке $F$ , лежащей внутри треугольника $ABC.$ Оказалось, что $∠ADE = ∠BDE, AF ⁄= BF$ и $∘ ∠AF B = 80$ . Найдите величину $∠ACB.$

Подсказки к задаче

Подсказка 1

Нам бы очень хотелось, чтобы треугольники △ADE и △BDE оказались равны... Красиво ведь: равные углы, общая сторона, но условие о паре не равных отрезков рушит нам всё! Если они не равные, то что интересного можно заметить про эту пару?

Подсказка 2

В геометрических задачах часто бывает полезно посмотреть на каждое данное условие: зачем оно здесь, что можно из него вытащить? Из этих соображений было бы полезно посмотреть на точку Е — она может дать нам много равных отрезочков!

Подсказка 3

Итак, у вышеупомянутой пары треугольников есть две пары соответственно равных стороны и равные углы, но углы эти не между соответственно равными сторонами. Призовём на помощь теорему синусов, чтобы установить соотношение углов в этих треугольниках.

Подсказка 4

Всё равно нам пока не видно как выразить искомый угол... Красивую гипотезу о том, что F может быть центром окружности мы отмели ещё на условии о неравенстве отрезков, а делать что-то всё равно нужно. Попробуем провести доп построение, чтобы получить ещё один вписанный угол, опирающийся на дугу AB: попробуйте продлить AF до пересечения со сферой.

Подсказка 5

Самое время использовать свойства вписанного четырёхугольника и ту самую связь углов, которую мы получили ранее. Двух пар соответственно равных углов и общей стороны треугольников вполне достаточно, чтобы сделать выводы о равенстве!

Подсказка 6

Видим красоту: в плоскости (АВС) внезапно появился равнобедренный треугольник с искомым углом при основании и известным внешним углом. Осталось лишь немного счёта и задача решена :)

Показать ответ и решение

$PIC$

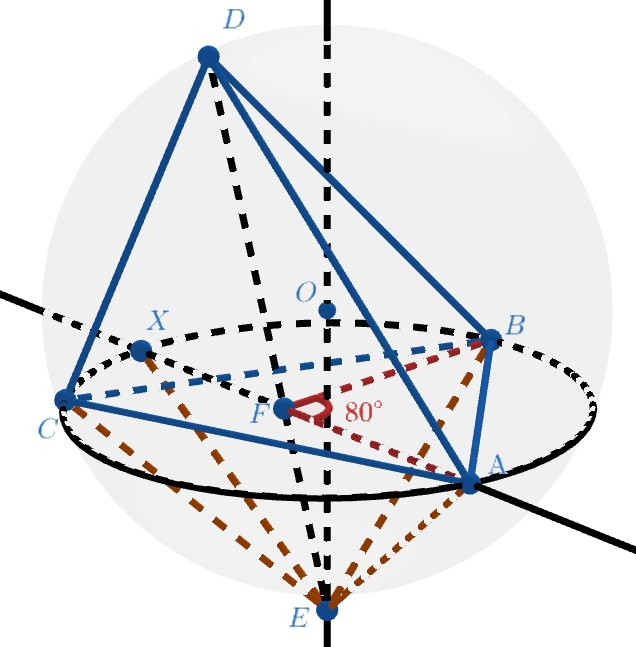
Первое решение.

Заметим, что точка $E$ равноудалена от точек $A,B,C$ , так ее проекция на плоскость $ABC$ совпадает с проекций точки $O$ на эту плоскость и является центром описанной окружности треугольника $ABC$ .

Рассмотрим треугольники $ADE$ и $BDE.$ Они имеют пару равных сторон $AE$ и $BE$ , общую сторону $DE$ и равные углы $ADE$ и $BDE.$ Из теоремы синусов следует, что эти треугольники либо равны, либо углы $DAE$ и $DBE$ дополняют друг друга до $180∘.$ Первая ситуация невозможна, так как в случае равенства треугольников $ADE$ и $BDE$ точки $A$ и $B$ равноудалены относительно любой точки на стороне $DE$ , но по условию $AF ⁄=BF.$ Значит, $∠DAE + ∠DBE = 180∘.$

Рассмотрим точку $X$ пересечения луча $AF$ со сферой $Ω$ , описанной около тетраэдра $ABCD.$ Заметим, что луч $AF$ лежит в плоскостях $ABC$ и $AED$ , а значит точка $X$ лежит на описанных окружностях треугольников $ABC$ и $AED.$ Точка $E$ равноудалена относительно всех точек описанной окружности треугольника $ABC;$ в частности, $AE = XE.$ Из вписанности четырехугольника $AEXD$ следует, что $∠DAE + ∠DXE = 180∘.$ Раз $AE = XE$ , то $E$ - середина дуги $AX$ описанной окружности треугольника $ADE$ , и значит $∠ADE =∠XDE$ .

Используя выведенные ранее равенства углов, заключаем, что треугольники $DBE$ и $DXE$ равны по второму признаку:

∠DBE = 180∘ − ∠DAE =∠DXE, ∠XDE = ∠ADE = ∠BDE,

сторона $DE$ – общая. Раз треугольники $DBE$ и $DXE$ равны, то вершины $B$ и $X$ равноудалены относительно любой точки на стороне $DE;$ в частности, $BF = FX$ .

Осталось посчитать углы в плоскости $ABC.$ Последовательно используя вписанность четырехугольника $ABXC$ , равнобедренность треугольника $BFX$ и теорему о внешнем угле для треугольника $BF X$ , пишем

∠ACB =∠AXB = 1⋅(∠FXB + ∠FBX )= 1⋅∠AF B = 40∘ 2 2

________________________________________________________________________________________

Второе решение.

Пусть луч $AF$ пересекает сферу $Ω$ , описанную около тетраэдра $ABCD$ , в точке $X$ . По построению точки $E$ верно соотношение $EX = EA$ , которое влечет за собой равенство $∠ADE = ∠EAF$ . Аналогичными рассуждениями получаем, что $∠BDE = ∠EBF$ , и, следовательно, $∠EAF = ∠EBF$ .

Обозначим точку пересечения прямой $OE$ с плоскостью $ABC$ , являющуюся центром описанной окружности треугольника $ABC$ , через $O1$ . Тогда $∠O1AE = ∠O1BE$ .

Рассмотрим трехгранные углы $AO1EF$ и $BO1EF$ . В них совпадают плоские углы $EAF$ и $EBF$ , плоские углы $O1AE$ и $O1BE$ и двугранные углы при ребрах $AO1$ и $BO1$ прямые. Следовательно, соответствующие трехгранные углы равны. А значит равны и плоские углы $∠FAO1 =∠F BO1$ . Отметим, что это равенство можно вывести и из теоремы косинусов для трехгранных углов. Указанное равенство возможно в двух случаях: либо точка $F$ лежит на серединном перпендикуляре к $AB$ (точки $A$ и $B$ симметричны относительно $FO1$ ), либо точка $F$ лежит на описанной окружности треугольника $ABO 1$ . Первый случай запрещен условием $AF ⁄= BF$ , значит, имеет место второй. Тогда $∠AOB = ∠AFB = 80∘$ и является центральным для угла $ACB$ в описанной окружности треугольника $ACB$ . В результате заключаем, что $∘ ∠ACB =40$ .

Ответ:

$40∘$

Следующая подтема