Жадные алгоритмы

Вспомним, как сравнивают числа. Сначала — количество разрядов (в нашем случае во всех числах по 6), а дальше — по разрядам слева направо. Тогда, каждый раз выбирая самый маленький доступный разряд, мы получим и самое маленькое число.

В разрядах могут стоять как максимум цифры 2, 9, 5, 9 соответственно. Однако, если первая цифра равна 2, то вторая не больше 3, и получается как максимум . Значит, в точности не достижимо, а вот число на 1 меньше мы уже получать умеем: 19:59 даёт сумму 24.

Для начала отметим, что жадность здесь не работает! Казалось бы, мы хотим, чтобы число содержало как можно меньше разрядов. Поэтому надо начать с 777, но тогда остается сумма 4, которую нельзя представить одной цифрой, являющейся простым числом. Поэтому будем решать задачу по-другому.

Сначала докажем, что в числе не может быть 4 или менее знаков. Трёх точно не хватит, так как максимальная сумма цифр . Далее рассмотрим четырёхзначные числа. Так как 25 — нечётное число, то 4 цифры не могут быть нечётными. Поэтому как минимум одна цифра равна 2, и тогда сумма оставшихся равна 23, и тремя цифрами, не превосходящими 7, её не получить.

Итак, в числе как минимум 5 знаков. Заметим, что 22777 подходит. При этом числа с одинаковым количеством разрядов мы сравниваем по цифрам слева направо, и цифра 2 — минимально возможная. Поэтому все числа, начинающиеся не на 22, будут больше нашего примера. Оставшиеся цифры равны по 7, так как сумму 21 можно получить только с помощью трёх семёрок.

Чем больше в числе разрядов, тем больше число. Поэтому мы хотим получить число наибольшей разрядности. Давайте жадно брать все единицы, чтобы получить максимальное количество разрядов. Так как каждая цифра хотя бы 1, то разрядов всегда не более 100. Пример на 100 разрядов единственный:

А теперь мы хотим как можно меньше разрядов в числе, то есть нужно брать как можно больше девяток. Так как каждая цифра , то всего разрядов , то есть . Теперь нужно сделать наименьший старший разряд (то есть хочется, чтобы на первом месте стояла 1). Пример на такие условия существует:

Хотим получить как можно больше девяток. В году мы можем получить максимум сумму цифр . В месяце максимальная сумма 9. В дате максимум . Осталось проверить, что такая дата, полученная жадным алгоритмом, действительно существует.

1) Больше всего у нас зеленых ягод (даже именно столько, сколько остальных в сумме). Поэтому давайте находить пары для зеленых. Всех зеленых можем соединить со всеми остальными цветами по парам. Получили вообще максимальное возможное количество разноцветных пар (50). Осталось проверить, что действительно все полученные пары разноцветные.

2) Давайте сначала оценим наименьшее возможное количество ходов:

. Теперь нужно попробовать добиться такого результата жадным алгоритмом. Давайте будем каждый раз брать по шарику из трех коробок с наибольшим количеством шариков. Получим:

(1, …, 7, 8, 9) -> (1, …, 6, 7, 8) -> (1, …, 6, 5, 6, 7) -> (1, …, 5, 5, 5, 5, 6) ->

(1, 2, 3, 4, 5, 5, 4, 4, 5) -> (1, 2, 3, 4, 4, 4, 4, 4, 4) -> (1, 2, 3, 3, 3, 3, 4, 4, 4) ->

(1, 2, 3, 3, 3, 3, 3, 3, 3) -> (1, 2, 2, 2, 2, 3, 3, 3, 3) -> (1, 2, 2, 2, 2, 2, 2, 2, 3) ->

(1, 1, 1, 2, 2, 2, 2, 2, 2) -> (1, 1, 1, 1, 1, 1, 2, 2, 2) -> (1, 1, 1, 1, 1, 1, 1, 1, 1) ->

(0, 0, 0, 1, 1, 1, 1, 1, 1) -> (0, 0, 0, 0, 0, 0, 1, 1, 1) -> (0, 0, 0, 0, 0, 0, 0, 0, 0)

Пронумеруем все строчки и все столбцы числами от 1 до 100. Тогда нам нужно попасть из клетки (1, 1) в клетку (100, 100). За каждый ход коня одна координата меняется на 1 (+1 или -1), а вторая на 2 (+2 или -2). Будем жадно прыгать к клетке (100, 100). Сначала в клетку (2, 3), потом в (4, 4). Будем продолжать такие прыжки по 2. Тогда получим последовательность клеточек:

(1, 1) -> (4, 4) -> (7, 7) -> …-> (3k + 1, 3k + 1) -> (3(k + 1) + 1, 3(k + 1) + 1) -> ...

Заметим, что закончим мы именно в клетке (100, 100), так как мы побываем на всех клетках вида (3k + 1, 3k + 1), а число 100 представляется в таком виде (дает остаток 1 при делении на 100).

Нам понадобилось ходов.

Проверим оценкой, что наш жадный алгоритм дал лучший результат. За один ход коня сумма координат клетки меняется не более, чем на 3. Тогда, чтобы из суммы 2 получить сумму 200, нужно как минимум ходов.

Покажем, как получить требуемое расположение за 154 хода, сделав хода по вертикали и 10 ходов по горизонтали. На четырех парах вертикалей поменяем фишки местами, как в предыдущей задаче, сделав 8 горизонтальных ходов. Два оставшихся горизонтальных хода израсходуем на последней вертикали: белая фишка на полпути пропускает чёрную и возвращается на вертикаль.

Теперь оценим. Из предыдущего решения ясно, что нужно не менее чем ход. Почему не хватит 153? После каждого хода число фишек на белых полях меняется на 1, поэтому его чётность меняется (происходит чередование). Но в начале и в конце на белых полях фишек поровну, поэтому нужно чётное число ходов.

Решение

Начальная идея: чтобы было много прямоугольников, они должны быть маленькими. Посмотрим на самые маленькие (самой маленькой площади) различные прямоугольники (и которые влезут в наш квадрат): , , , , , , . Сумма площадей перечисленных прямоугольников как раз 25, хочется всех их расположить в нашем квадрате. А это возможно!

Сначала оценим наименьшее число ходов. Чтобы попасть на противоположную сторону доски, фишке надо сделать семь вертикальных ходов. Но хотя бы одна из двух фишек, стоящих на одной вертикали, должна сделать горизонтальный ход (иначе им не разминуться). Поэтому вместе эти фишки сделают не менее 15 ходов. А таких пар на доске восемь. Значит, менее чем за 120 ходов добиться требуемой расстановки нельзя.

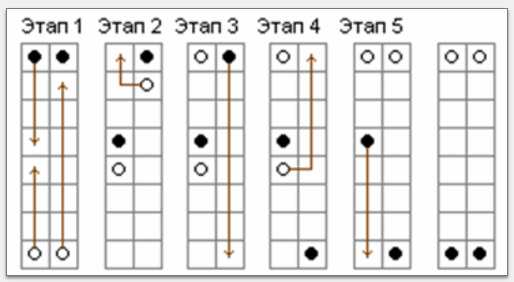
Придумаем алгоритм. Разобьём фишки на четвёрки, стоящих на двух соседних вертикалях. Каждую четвёрку передвинем за 30 ходов так, как показано на рисунке:

"Потери"на горизонтальные ходы происходят только на втором и четвёртом этапах.