Теорема косинусов и теорема Пифагора
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Вписанная в прямоугольный треугольник окружность касается катетов
и
в точках
и
Найдите
если
известно, что
Источники:
Подсказка 1
Для нашего удобства обозначим CD = x, BF = y, AD = z. Также отметим, что E — точка касания окружности с гипотенузой треугольника. Какие равенства можно записать в первую очередь?
Подсказка 2
Помним, что отрезки касательных из одной точки равны, и записываем теорему Пифагора! Получится довольно интересное уравнение, в котором так и захочется привести подобные…а как использовать синус?
Подсказка 3
Приведя подобные слагаемые, мы приходим к тому, что x/y * x/z + x/y + x/z = 1. Тут есть одинаковые множители, которые так и хочется вынести)
Подсказка 4
(x/y + 1)(x/z + 1) = 2. Осталось лишь понять, как же нам выразить z через x, а в этом нам поможет условие, а именно — тангенс известного угла!
Положим . Тогда
, где
точка касания окружности с гипотенузой.
![]()
По теореме Пифагора .
Раскрывая скобки и приводя подобные слагаемые, получаем или, что то же самое,
Раскладывая на множители, получаем
По условию . Тогда
и
. Стало быть,
, откуда
.
Подставляя в полученное выше соотношение, получаем
. Тогда
, откуда
.
Ошибка.
Попробуйте повторить позже
В окружность радиуса вписан четырехугольник с перпендикулярными диагоналями, которые равны
и
. Найдите стороны
этого четырехугольника.
Подсказка 1
Вот если бы мы знали отношения, в которых диагонали делятся точкой пересечения, то просто бы теоремой Пифагора посчитали стороны! Будем целиться в нахождение этих кусочков диагоналей! Ещё вопрос: как использовать радиус? Теорема синусов? На диагонали опираются не самые полезные углы, а больше длин мы не знаем. Похоже, придётся центр окружности отметить и провести радиус хотя бы к паре вершин. Так, имеем длину диагоналей (по факту хорд в окружности) и центр —> какая конструкция напрашивается?
Подсказка 2
Проведём из центра окружности перпендикуляры на диагонали! Они ведь в серединку попадут! Мы знаем радиус и середину стороны —> найдём эти перпендикуляры —> найдём нужные нам кусочки диагоналей (заметьте, что при проведении двух перпендикуляров, учитывая прямой угол между диагоналями, у нас образовался прямоугольник внутри!)
![]()
Пусть диагонали и
пересекаются в точке
, а
— середины
и
соответственно. Не умаляя общности,
можно считать, что
лежит на отрезке
, а
— на
, поскольку иначе можно поменять местами пары вершин четырёхугольника
на диагоналях. Известно, что из центра окружности перпендикуляр к хорде проходит через её середину. Тогда
прямоугольник (не
забываем, что ещё диагонали перпендикулярны). По теореме Пифагора
Аналогично,
Итак, мы знаем кусочки диагоналей после разбиения точкой пересечения. Осталось посчитать стороны четырёхугольника по теореме Пифагора:
Ошибка.
Попробуйте повторить позже
Пункт а, подсказка 1
Запишем условие: AD = x, AC = 3x. Попробуем сразу воспользоваться касательной — сможем отметить равные углы и посчитать длину касательной. Что из этого можно вывести?
Пункт а, подсказка 2
Треугольники ABD и ACB подобны, а AB = sqrt(3) * x. Отсюда несложно вывести BC/BD!
Пункт б, подсказка 1
Подумаем, а зачем нам дали косинус угла A? В каких треугольниках есть угол A и что в них можно найти?
Пункт б, подсказка 2
Воспользуемся теоремой косинусов и найдем BD! Что еще можно найти на основе полученных выводов? А в какой теореме фигурирует радиус окружности?
Пункт б, подсказка 3
Из пункта а) мы с легкостью можем найти BC! А радиус окружности фигурирует в теореме синусов. Только вот нам не хватает синуса угла C…а как можно найти его? Как его связать с углом A?
Пункт б, подсказка 4
Воспользуемся теоремой синусов для треугольника ABC!
Пусть
![]()
По теореме об отрезках секущих
Далее , откуда
. Далее найдём
по теореме косинусов
Из подобия сразу же получаем , теперь используем теорему синусов для
Поскольку , то
.
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике с боковой стороной, равной 4, проведена медиана к боковой стороне. Найдите основание треугольника, если медиана равна 3.
Пусть дан треугольник
— середина
![]()
Напишем теорему косинусов для треугольника :
Значит, и
Теперь напишем теорему косинусов для треугольника .
Ошибка.
Попробуйте повторить позже
В треугольнике отрезок
— медиана,
. Найдите угол
.
Удвоим медиану до точки
. Тогда
,
и
.
![]()
Значит, . Напишем для треугольника
теорему
косинусов.
Ошибка.
Попробуйте повторить позже
Две окружности одинакового радиуса пересекаются в точках
и
. На первой окружности выбрана точка
, а
на второй - точка
. Оказалось, что точка
лежит на отрезке
, a
. На перпендикуляре к
,
проходящем через точку
, выбрана точка
так, что
(точки
и
расположены по разные стороны от прямой
.
а) Найдите длину отрезка .
б) Пусть дополнительно известно, что . Найдите площадь треугольника
.
Источники:
Подсказка 1
Самая естественная мысль, которая возникает это найти отрезок из теоремы Пифагора. Тогда нам нужно найти два катета. Подумаем, как удобнее всего выразить сторону в треугольнике, если мы знаем радиус описанной окружности?
Подсказка 2
Верно, их можно выразить через теорему синусов. Для этого нам осталось только обозначить удобный угол и найти стороны.
Подсказка 3
Теперь попробуем ввести ещё один угол бетта, равный углу BCF, и узнать углы треугольника АDС. Что можно сказать про тангенс угла бетта, как можно выразить его через отрезки?
Подсказка 4
Ага, понимаем, что тангенсы углов BCF и DAB равны, а значит и углы эти равны. Теперь осталось выразить сторону АС треугольника АCF и найти его площадь.
![]()
а) Пусть - радиусы данных в условии окружностей,
. Тогда
, и по теореме синусов для
:
для :
Значит,
откуда
б) Так как , то
. Далее, углы
и
вписаны в равные окружности и опираются на одну
и ту же хорду
, поэтому они равны, и из прямоугольного треугольника
находим, что
.
Тогда
поэтому
Итак,
, где Значит,
а)
б)
Ошибка.
Попробуйте повторить позже
а) Две параллельные прямые и
касаются окружности
с центром
в точках
и
соответственно. Окружность
с
центром
касается прямой
в точке
, пересекает прямую
в точках
и
, а также вторично пересекает
окружность
в точке
(при этом точка
лежит между прямыми
и
). Известно, что отношение площади
четырёхугольника
к площади треугольника
равно 2. Найдите отношение радиусов окружностей
и
б) Найдите эти радиусы, если дополнительно известно, что .
Источники:
Пункт а, подсказка 1
Рассмотрите прямые углы.
Пункт а, подсказка 2
Пусть ∠O₁BO₂ = α. Выразите через него другие углы.
Пункт а, подсказка 3
Запишите отношение площадей четырёхугольников. Поскольку мы хотим найти отношение радиусов, их надо использовать при вычислениях.
Пункт б, подсказка 1
Рассмотрите треугольник ABD.
![]()
а) Пусть - радиусы окружностей
,
соответственно,
, а прямые
и
пересекаются в точке
. Тогда из
условия касания
(
— диаметр) и
, откуда
, а
. Треугольники
и
равны по трем сторонам, поэтому
. Площадь треугольника
равна
. Применим данное в условии отношение площадей
и
. Кроме того, как расстояния между прямыми, равны
, откуда
, следовательно
, и
.
б) Из прямоугольного треугольника получаем
, то есть
. Итак,
и
.
Отсюда
.
а) ; б)
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике на стороне
выбрана точка
так, что
Из точки
опущены
перпендикуляры
и
на стороны
и
соответственно. При этом
. Найдите
.
Источники:
Подсказка 1
Сначала стоит обратить внимание на QK, ведь это и медиана, и высота в △BQC. Делаем вывод про △BQC, а дальше, конечно, надо бы ввести какие-нибудь удобные обозначения для отношений на сторонах AB и AC!
Подсказка 2
Например, положим AQ = a и AM = b. Как мы вообще собираемся считать отношение MK:AC? Кажется, что мы хотим выразить MK и AC через какую-то одну переменную, тогда она при делении сократится. Значит, надо найти связь между a и b! Что из условия ещё остаётся неиспользованным?
Подсказка 3
Конечно же, перпендикулярность QM и AB! Попробуйте использовать образовавшиеся прямоугольные треугольники, чтобы найти эту самую связь между a и b. Может, это ещё натолкнёт вас на какой-нибудь крутой факт про BQ...
Подсказка 4
Действительно, проведя расчёты, получим, что BQ ⊥ AC. Теперь снова обратим внимание на △BQC. Помимо того, что он равнобедренный, теперь мы ещё знаем, что он прямоугольный, значит, углы при гипотенузе хорошие! Только вот как это можно использовать? Поскольку сторона AC выражается через a, то мы хотим выразить MK тоже через a. Может быть, теорема косинусов? Там как раз можно будет использовать найденный хороший угол! Только надо сначала сформировать подходящий треугольник.
Подсказка 5
А именно, проведём прямую, параллельную AC, через точку M, тогда образуется треугольник, высеченный этой прямой и MK. Осталось в нём найти стороны и использовать теорему косинусов!
![]()
Раз и медиана, и высота в треугольнике
, то он равнобедренный, и значит,
. Пусть
и
. Тогда
и
. Так как
, то
. Значит,
. Тогда
. Значит,
![]()
Проведем через прямую параллельную
. Мы знаем, что
и
, поэтому
и
и
. Из параллельности
, поэтому
,
и
. Тогда по теореме косинусов
Тогда
Ошибка.
Попробуйте повторить позже
Окружность, проходящая через вершины и
прямоугольника
, пересекает сторону
в точке
, а диагональ
– в точке
. Найдите площадь четырёхугольника
, если
, а точки
лежат на одной
прямой.
Источники:
Подсказка 1
Поскольку ABEF не является какой-нибудь "удобной" фигурой, её площадь удобнее всего искать как разность площадей знакомых нам фигур: например, △ABC и △CFE. Для этого нам понадобятся ещё длины сторон. Будем их искать!
Подсказка 2
Какие свойства вписанного четырёхугольника вы помните? Сделайте вывод об ∠АFE, пользуясь вписанностью ABEF. Отметьте всевозможные равные углы и обратите внимание на прямоугольные треугольники в нашей конструкции — что можно про них сказать?
Подсказка 3
Поработайте с подобием прямоугольных треугольников: зная отношение катетов и гипотенузу, длина которой дана в условии, Вы можете отыскать и сами эти катеты (Пифагор в помощь!). Останется лишь дважды применить формулу площади прямоугольного треугольника и задача убита!
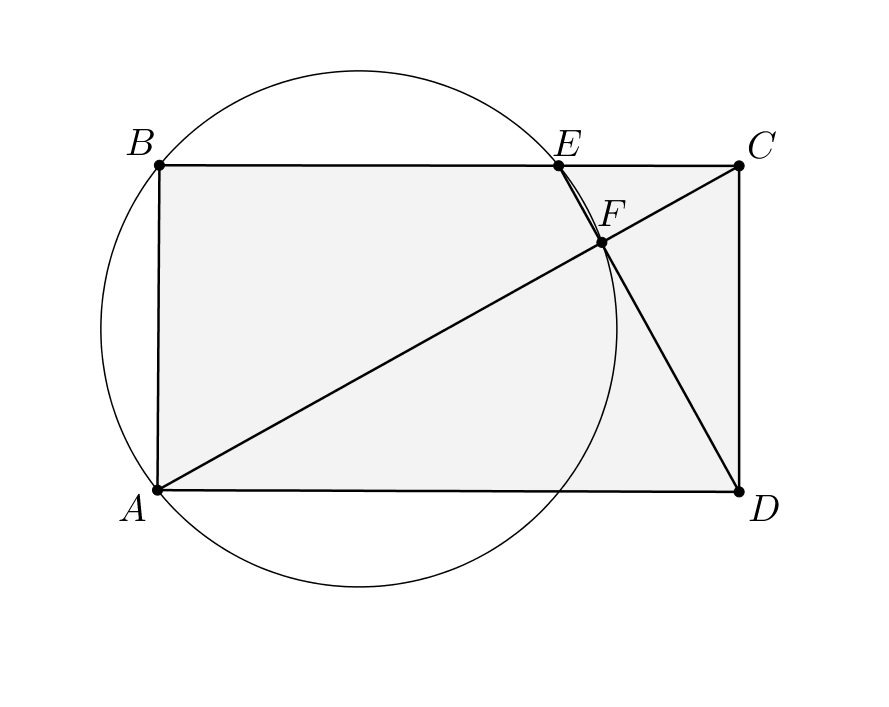
Поскольку четырёхугольник вписан в окружность, угол
прямой. Следовательно, треугольники
,
,
подобны. Поскольку
,
, то
. Из подобия
, откуда
. По теореме
Пифагора для
,
, откуда
и из теоремы Пифагора для
получаем
. Стало быть, площадь
Далее, из того же подобия следует, что
. Стало быть,
Тогда площадь
четырёхугольника
равна
.
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике на высоте
, равной основанию
, как на диаметре построена окружность, пересекающая
боковую сторону
в точке
. Каково отношение площади треугольника
к площади треугольника
Какая часть площади
треугольника
находится внутри окружности?
Источники:
Подсказка 1!
Давайте обозначит CF за x и попробуем посмотреть, что у нас получается. Основание треугольника обозначим за 2a. Давайте обозначим еще оснаток BF за y. Мы знаем, что трегуольник BFH прямоугольный, тогда давайте воспользуемся теоремой о соотношении катетов в прямоугольном треугольнике! Попробуйте найти отношение y/x.
Подсказка 2!
Да, записав теорему мы получим, что это соотношение равно 4. Осталось только найти соотношение площадей)
Подсказка 3!
Так, займемся пунктом b. Было бы здорово попробовать избавиться от x и выразить его через a. Для нахождения площади сегментов окружности, нам придется обратиться к цглам и центру. Отметьте центр окружности и заметим, что тогда в треугольнике BOF можно написать теорему косинусов! Остается аккуратно посчитать и ответить на вопрос.
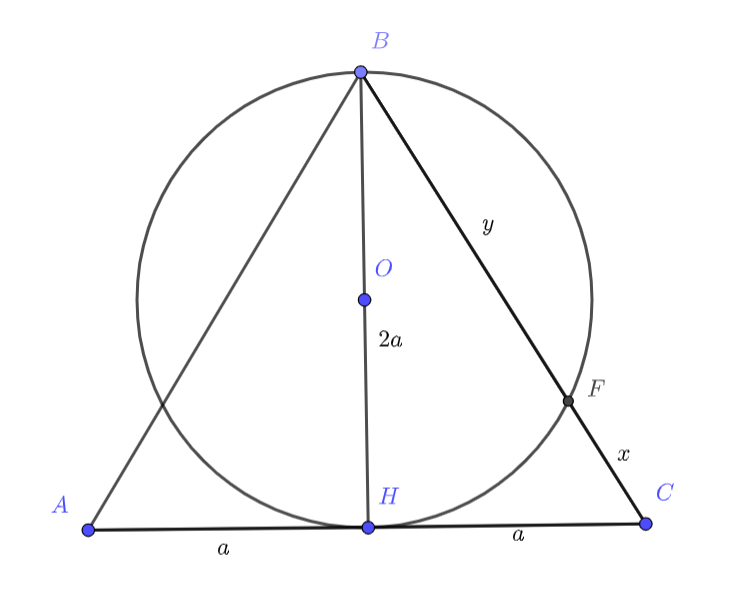
Введем обозначения: . Поскольку угол
- прямой, то по теореме об соотношениях в прямоугольном
треугольнике для двух катетов
будем иметь:
Из отношения площадей треугольников с общим углом находим ответ на первый вопрос:
Из теоремы Пифагора для имеем
. Далее пусть
— центр окружности из условия, а также
, запишем теорему косинусов для
Обозначим площадь сектора через
. Тогда
. Внутри окружности у треугольника два таких сектора. Кроме
того, внутри окружности два треугольника одинаковой площади (симметрия относительно
). Найдем площадь
. Тогда ответ на второй вопрос будет следующий:
.
Ошибка.
Попробуйте повторить позже
В окружность радиуса 13 вписаны трапеция
и прямоугольник
таким образом, что
Найдите отношение площади
к площади
если известно, что
Источники:
Подсказка 1
Хм, нам даны хорды и радиус, к тому же, несколько прямых перпендикулярны. Попробуйте перейти к прямоугольным треугольникам.
Подсказка 2
Может, надо сделать некоторое дополнительное построение?
Подсказка 3
Воспользуйтесь тем, что диаметр, перпендикулярный хорде, делит её пополам.
Подсказка 4
Рассмотрите углы между диагоналями в четырёхугольниках.
Проведём через центр окружности прямую, перпендикулярную основаниям трапеции. Пусть она пересекает
и
в точках
и
соответственно.
![]()
Так как диаметр, перпендикулярный хорде, делит эту хорду пополам, и
. По теореме Пифагора из
треугольников
и
находим, что
и
. Отсюда
или
Заметим, что так как диагонали трапеции перпендикулярны диагоналям прямоугольника, то углы между диагоналями в обеих этих фигурах одинаковы. Так как площадь четырехугольника равна произведение его диагоналей, то теперь нам нужно посчитать
Пусть . Заметим, что
. Значит,
. По теореме Пифагора
и так
как
, то
. Отсюда
Пусть . Заметим, что
. Значит,
. По теореме Пифагора
и так как
,
то
. Отсюда
Ошибка.
Попробуйте повторить позже
Хорды и
окружности
с центром
имеют длину 4. Продолжения отрезков
и
соответственно за точки
и
пересекаются в точке
. Прямая
пересекает отрезок
в точке
, причём
a) Найдите
б) Пусть дополнительно известно, что радиус окружности равен 3, а точка
— центр окружности, вписанной в треугольник
Найдите длину отрезка
и площадь треугольника
Источники:
Пункт а, подсказка 1
Рассмотрите треугольник APD.
Пункт а, подсказка 2
Какое свойства для секущих окружности Вы знаете?
Пункта а, подсказка 3
В данном случае, PA ⋅ PB = PD ⋅ PC. Так как AB = CD, AP = PD. А чем будет являться четырёхугольник ABCD?
Пункта а, подсказка 4
Это равнобедренная трапеция. Нам дано отношение AL к LC, может, это намёк?
Пункт а, подсказка 5
Есть ли равные треугольники на картинке?
Пункт а, подсказка 6
Докажите, что PO — это биссектриса.
Пункт б, подсказка 1
Нам дали информацию о вписанной окружности треугольника ACP. какое дополнительное построение можно сделать?
Пункт б, подсказка 2
Рассмотрите биссектрису ∠CAP.
Пункт б, подсказка 3
Вспомните, что равные углы опираются на равные дуги.
Пункт б, подсказка 4
Докажите, что точка T лежит на окружности.
Пункт б, подсказка 5
Рассмотрите степень точки P (отношение секущих, проведенных из неё).
a) Раз хорды равны и их продолжения пересекаются, то — равнобедренная трапеция, у которой равны углы при основании, поэтому
— равнобедренный треугольник. Следовательно, треугольники
и
равны по трём сторонам, так что
— биссектриса.
По свойству биссектрисы
откуда
и значит,
![]()
б) Проведем биссектрису угла и пересечем ее с окружностью в точке
. Заметим, что угол
равен дугам
. Значит, половина угла
равна углу
и равна дугам
. Значит,
это середина
дуги
. Так же биссектриса угла
проходит через
. Значит,
.
Степень точки равна
. Отсюда
и
Посчитаем через теорему косинусов косинус угла .
Ошибка.
Попробуйте повторить позже
Равнобедренный треугольник с основанием
вписан в окружность
Хорды
и
параллельные прямой
пересекают сторону
в точках
и
соответственно, и при этом
. Найдите радиус окружности
и площадь
треугольника
если
а центр
окружности
расположен между прямыми
и
Источники:
Подсказка 1
Хм, даны равные отрезки на прямой. Какое дополнительное построение напрашивается?
Подсказка 2
Проведите прямую BO.
Подсказка 3
Образуется много прямоугольных треугольников. А может ли нам помочь теорема Пифагора?

Прямая перпендикулярна хордам
и делит каждую из них пополам. Пусть точки
,
и
середины
и
Обозначим радиус окружности
за
Тогда
и по теореме
Пифагора для треугольников
и
получаем
откуда после раскрытия скобок и
приведения подобных слагаемых следует, что
находим, что ,
. Тогда
;
Вычитая из первого уравнения второе, находим, что ,
. Тогда
Следовательно, .
Ошибка.
Попробуйте повторить позже
Диагонали трапеции взаимно перпендикулярны, а боковые стороны образуют угол . Основания имеют длины
и
Найдите высоту
трапеции.
Подсказка 1
Нам нужно найти высоту трапеции. Давайте подумаем, как это будет проще всего сделать. Например, если обозначить угол между основанием и диагональю за α, то высота это BD * sinα. А как можно выразить диагональ, зная угол?
Подсказка 2
Ага, так как диагонали перпендикулярны, то образуются прямоугольные треугольники, и все отрезки диагоналей легко выражаются через α. Выходит, что высота это 8cos(α)sin(α). Теперь наша задача найти угол α. Какое дополнительное построение удобно сделать в данном случае, зная угол между боковыми сторонами?
Подсказка 3
Верно, давайте достроим нашу трапецию до параллелограмма. Получается треугольник с углом при вершине в 30 градусов. Заметим, что все его стороны мы можем выразить из прямоугольных треугольников внутри трапеции, используя только угол α. Какой добивающей теоремой теперь можно воспользоваться?
Подсказка 4
Да, воспользуемся теоремой косинусов, потому что все стороны и угол в 30 градусов нам известны. Осталось только аккуратно найти α и выразить высоту. Победа!

Пусть эта трапеция . При этом
, а также
.
Построим , тогда
,
. Кроме того, из
получаем
. Введём также
. Используем прямой угол между диагоналями
. Отсюда
,
(
). Теперь мы готовы
написать теорему косинусов для
Оба значения подходят, поскольку обозначения в условии симметричны. Не умаляя общности, , откуда
. Осталось заметить, что высота трапеции равна
Ошибка.
Попробуйте повторить позже
В треугольнике стороны
и
соответственно равны 3 и
Биссектриса
равна
Найдите угол
Источники:
Подсказка 1
Воспользуйтесь золотым свойством биссектрисы.
Подсказка 2
Используйте теорему косинусов для треугольников, связанных с биссектрисой, например таких, как ABD...
Подсказка 3
Из полученной системы выразите сторону AC.
Подсказка 4
А теперь подставив в одно из уравнений, получите значения cos∠BAC. Осталось записать ответ через arccos) Успехов!
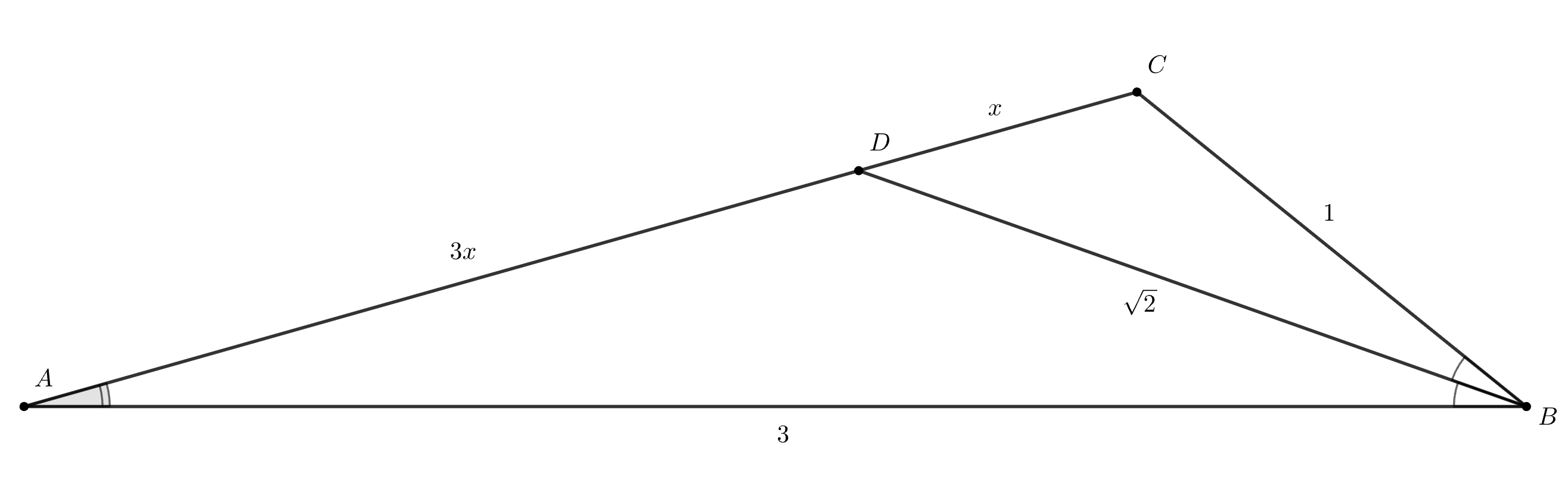
По свойству биссектрисы для некоторого
. Запишем теоремы косинусов для
и
:
Тогда из (1)
Ошибка.
Попробуйте повторить позже
На плоскости задана точка . Рассматриваются различные равносторонние треугольники
, такие что
Какое
максимальное значение может принимать длина отрезка
Источники:
Счётный способ, подсказка 1
Заметим, что если зафиксировать треугольник PAB, то картинка определяется единственным образом. Как его зафиксировать?
Счётный способ, подсказка 2
Конечно, можно ввести лишь три его стороны, но лучше ввести еще и два угла, чтобы счет проходил легче(а с помощью теорем синусов или косинусов, мы всегда сможем связать углы со сторонами при желании).
Счётный способ, подсказка 3
Выразите сторону AB по теореме косинусов и угол PBA через стороны треугольника PAB и угол APB. Выразили? Кажется, все готово, чтобы считать PC.
Счётный способ, подсказка 4
Попробуйте привести выражение PC к такому виду, чтобы только одно слагаемое было переменным, а все остальное являлось константой.
Геометрический способ, подсказка 1
На картинке есть угол 60 градусов и два равных отрезка исходящих из него(AB и AC). Это очень сильно намекает на поворот в этой точке.
Геометрический способ, подсказка 2
Да, нужно сделать поворот на 60 градусов, переводящий точку B в точку C. Это удобно, так как точка P переедет в точку P’,при этом APP’-равносторонний и треугольники AP’C и APB равны. Какой вывод о длине PC можно сделать?
Геометрический способ, подсказка 3
Да, по неравенству треугольника PC<=5. Осталось лишь привести пример, но как? Попробуйте делать те же действия, как вы получили оценку, но в обратном порядке, не забывая о том, когда эта оценка достигается(расположение точек P,P’,C)
—
Геометрический способ, подсказка 4
Точки P,P’,C лежат на одной прямой. Осталось в явном виде посчитать все отрезки на картинке, чтобы понять, что неравенство треугольника выполнено(или нужно показать ,как вы строили эту картинку и что все отрезки будут иметь длину как в условии).
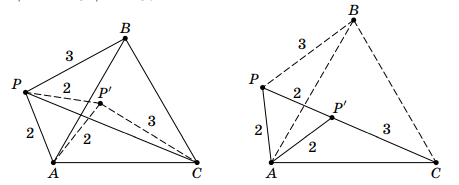
Первое решение.
Докажем, что длина не больше . Для этого рассмотрим поворот с центром в точке
на
таким образом, что
переходит в
.
Точка
переходит в
, а поскольку
и
, то
, откуда
по
неравенству треугольника.
Для построения примера сначала построим правильный , затем на продолжении
отметим
. Наконец, построим
правильный треугольник
на отрезке
. Остаётся показать, что выполнено
, но для этого достаточно рассмотреть поворот
на
в обратную сторону
, тогда отрезок
перейдёт в
.
Второе решение.
Просто посчитаем. Пусть ,
. Тогда из треугольника
из теоремы косинусов
следует
Теперь из треугольника по теореме косинусов
Ошибка.
Попробуйте повторить позже
Кратчайшее расстояние от вершины треугольника
до точек противолежащей стороны равно
. Найдите стороны
и
этого треугольника, если
и
Источники:
Подсказка 1
Какие есть вариации картинки из задачи, что в ней надо зафиксировать?
Подсказка 2
Например, надо рассмотреть случай, когда углы A и C — острые. Может ли в этом случае H лежать на AC?
Рассмотрим три возможных случая.
1) Углы и
острые.
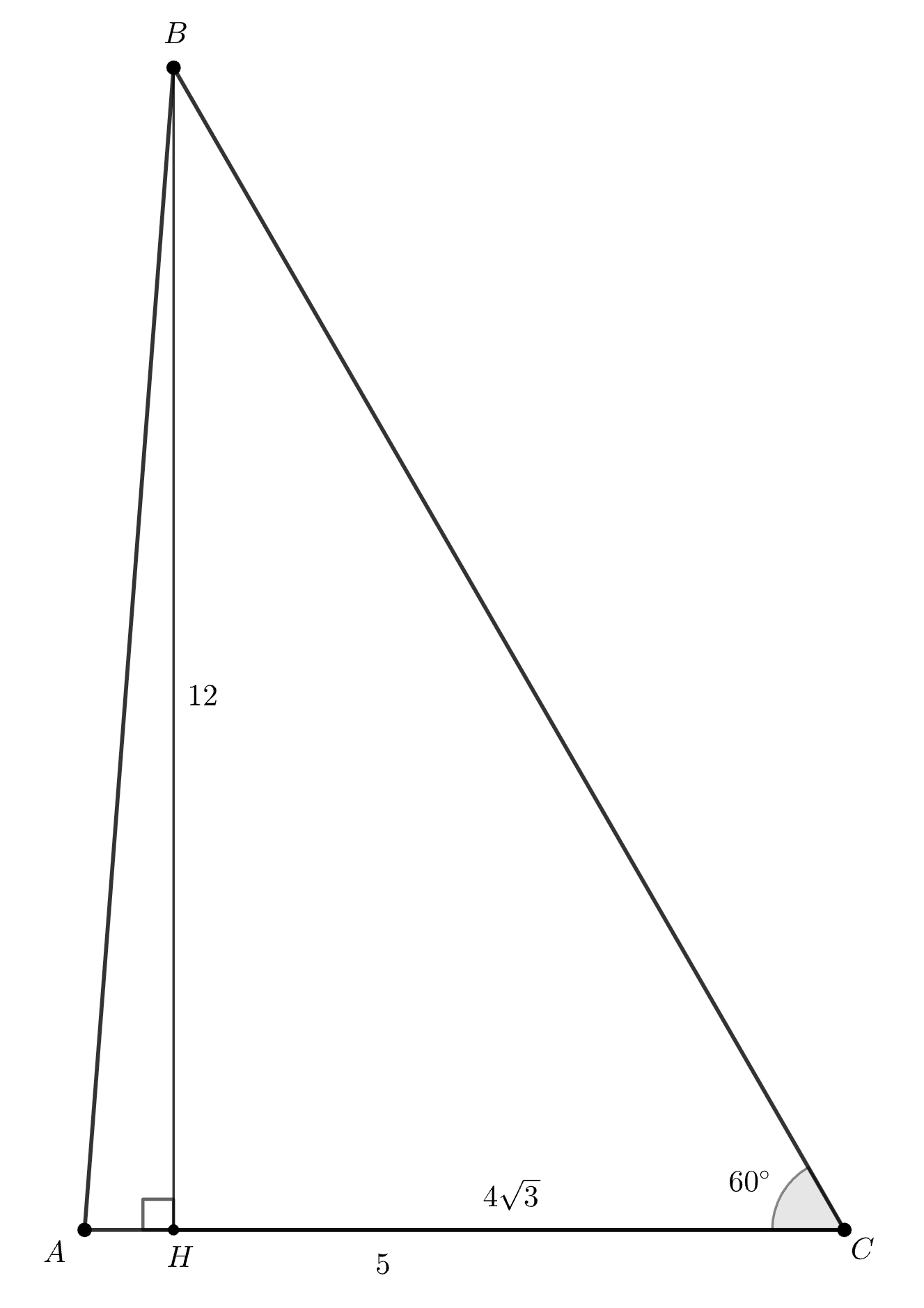
Тогда и высота
равна 12. Но в этом случае
и основание
высоты не может лежать на стороне
2) Угол тупой, а угол
острый.
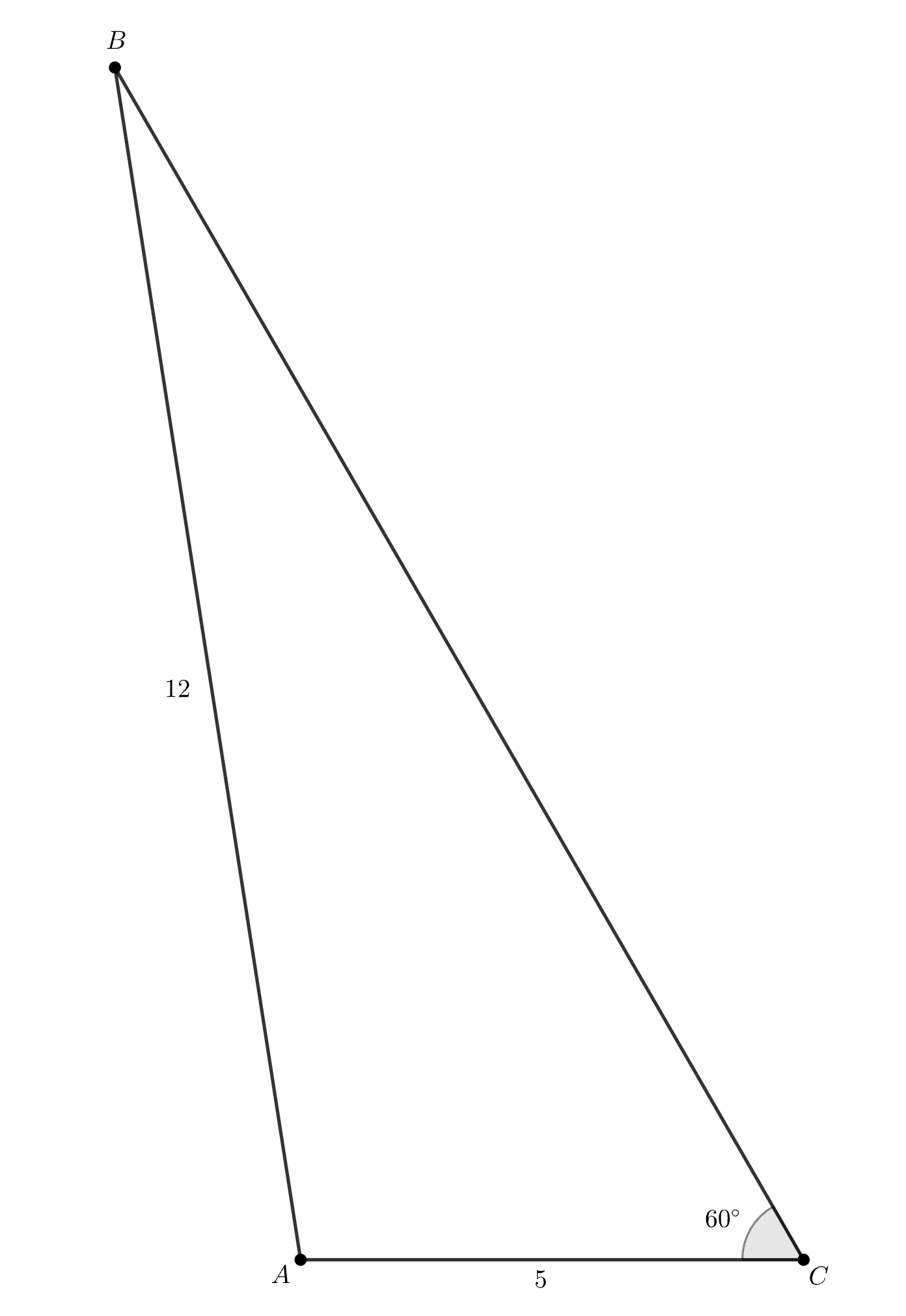
Тогда и по теореме косинусов
3) Угол острый, а угол
тупой.
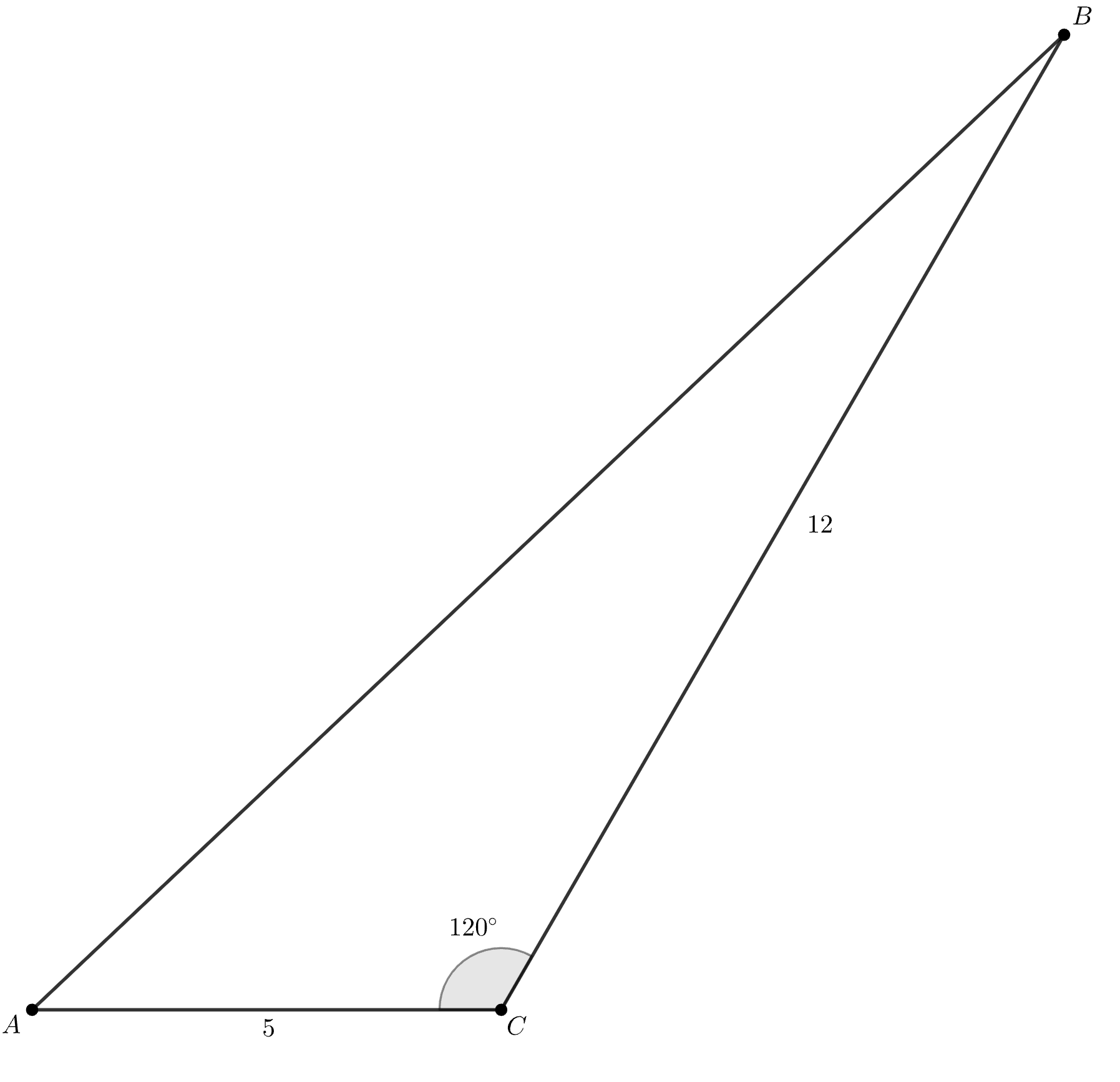
Тогда и по теореме косинусов
одна сторона равна а другая равна либо
либо
Ошибка.
Попробуйте повторить позже
В окружности диаметр и хорда
пересекаются в точке
под прямым углом. Найдите длину биссектрис треугольника
если
,
Источники:
Подсказка 1
По сути, всё, что у нас сейчас есть на картинке — это два прямоугольных подобных треугольника PAC и QCB, у которых известная одна сторона, а также есть равенство из того, что это пересекающиеся хорды в окружности. Вы скажете, что это одно и тоже, но плюс в том, что у нас ещё появляется отношение AP к QB, которые, в свою очередь, удачно выражаются через стороны треугольника, хорды ведь пересекаются под прямым углом. Попробуйте применить рассуждения выше к тому, чтобы выразить все отрезки через некоторый в этой задаче (мы же поняли, что она счётная на подобия, поскольку у нас в условии есть только окружность и хорды).
Подсказка 2
Удобным здесь будет взять за х отрезок BC, поскольку именно он меньше в 8 раз отрезка AC. Тогда, чтобы выразить все отрезки хорд, остается лишь записать равенство на произведение отрезков хорд (или, говоря умными словами, расписать степень точки C относительно нашей окружности).
Подсказка 3
В силу наличия отношения уже указанных сторон, связанного с подобием, у нас есть равенство на х, откуда он находится. Значит, мы нашли все отрезки хорд и картинка фиксирована. Значит, мы можем найти все отрезки треугольника из условия. Остается только вспомнить формулу биссектрисы и факт про отношения на которые разбивает биссектриса сторону, и задача решена!
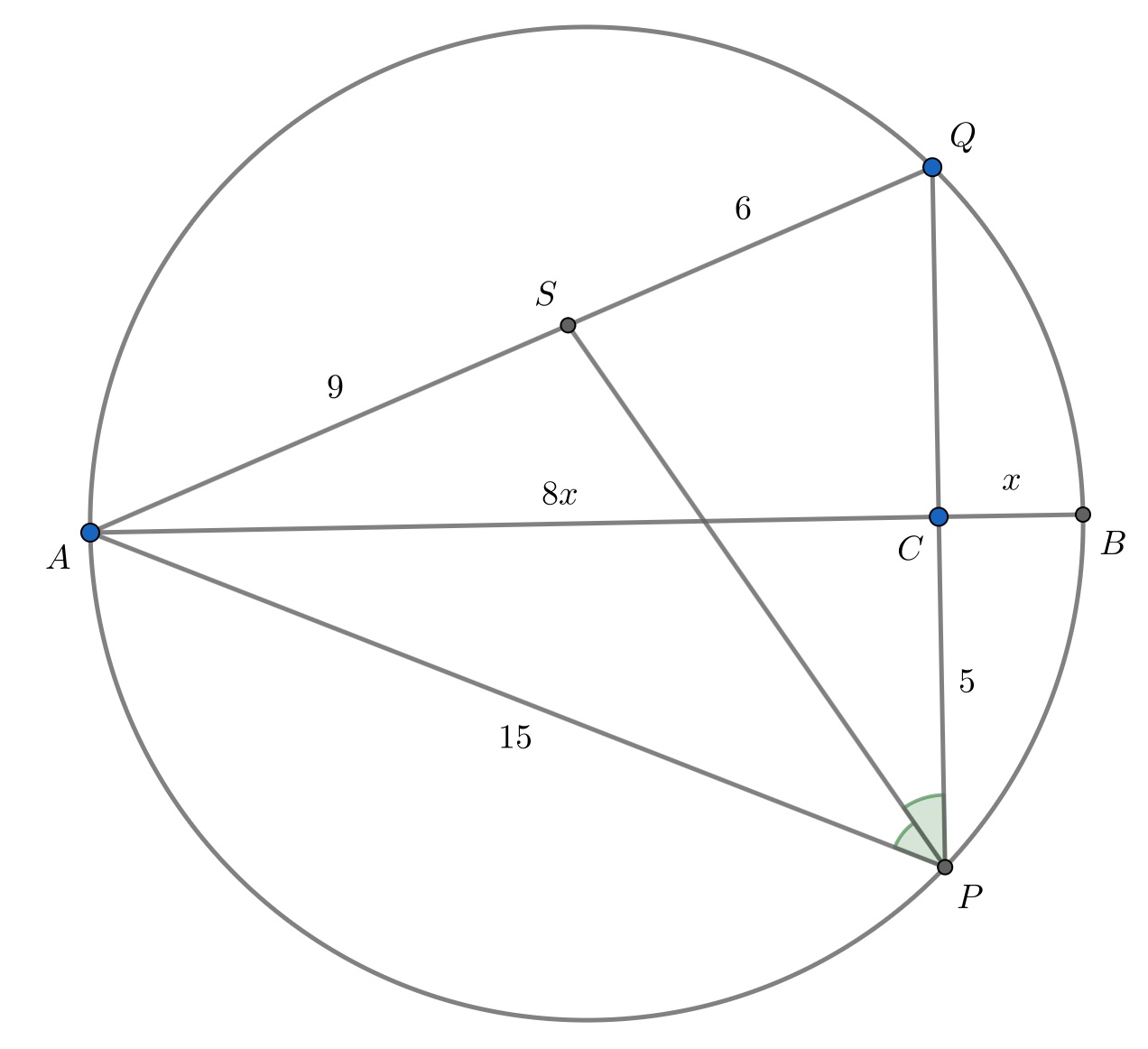
Обозначим тогда
и из
получаем, что
Поскольку
равнобедренный, то
биссектриса угла
и
По теореме Пифагора
Пусть биссектриса угла
пересекает
в точке
Taк как
то по свойству биссектрисы получаем:
Из
по
теореме косинусов получаем, что
Ошибка.
Попробуйте повторить позже
Даны две пересекающиеся окружности радиусов см и
см, расстояние между центрами которых равно 5 см.
![]()
Прямая пересекает эти окружности в точках и
так, как это показано на рисунке, причём длины отрезков
и
равны. Найти длину этих отрезков.
Задача 1
Чтобы стало проще жить, введём некоторые обозначения. Пусть 2 * x — величина, которую просят найти по условию задачи, p и q — длины перпендикуляров из центров окружностей к AD. Теперь вспомнив теорему Пифагора, мы можем записать систему из 3 уравнений для нахождения x, p и q.
Задача 2
Подставив два уравнения в третье, мы получаем уравнение на x, которое легко сводится к биквадратному. Осталось его решить!
Обозначим длины искомых отрезков за , отметим центры
и
окружностей и опустим из них перпендикуляры
и
на
прямую
, обозначим их длины за
и
соответственно.
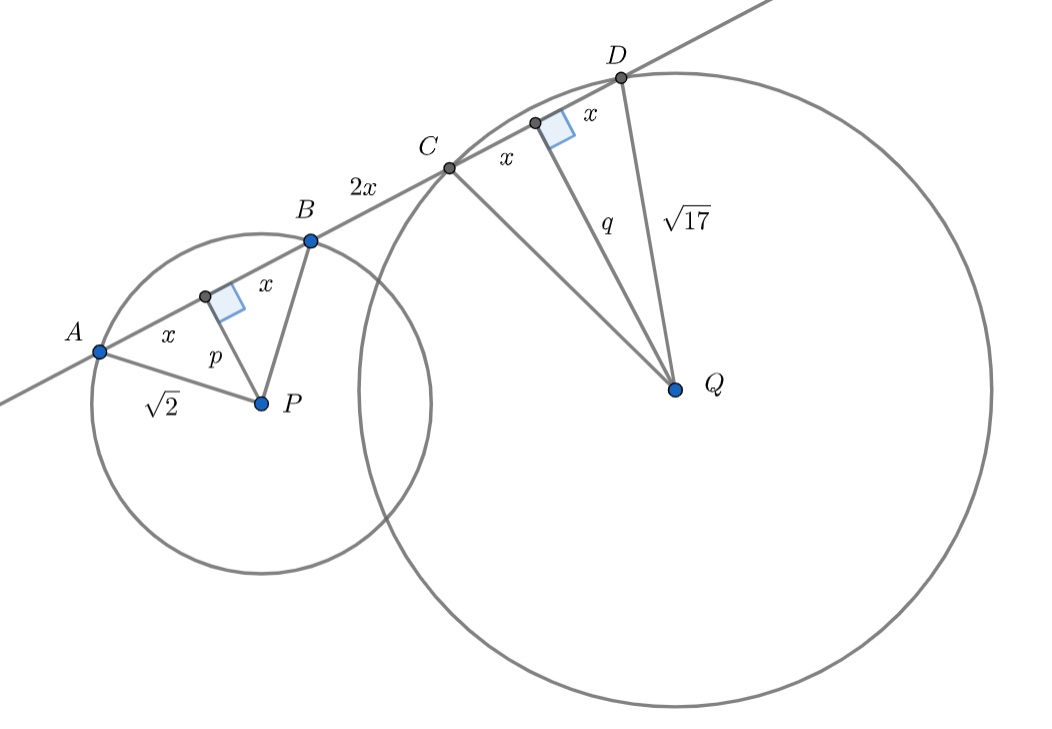
По теореме Пифагора имеем:
Отсюда
преобразуем это уравнение в биквадратное
Находим
поэтому единственный положительный корень . Следовательно, длины отрезков
и
равны 2 см.
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике основание
равно
угол
равен
. Точка
лежит на стороне
так, что
площадь треугольника
вчетверо больше площади треугольника
Найдите расстояние от точки
до прямой
и радиус
окружности, описанной около треугольника
Источники:
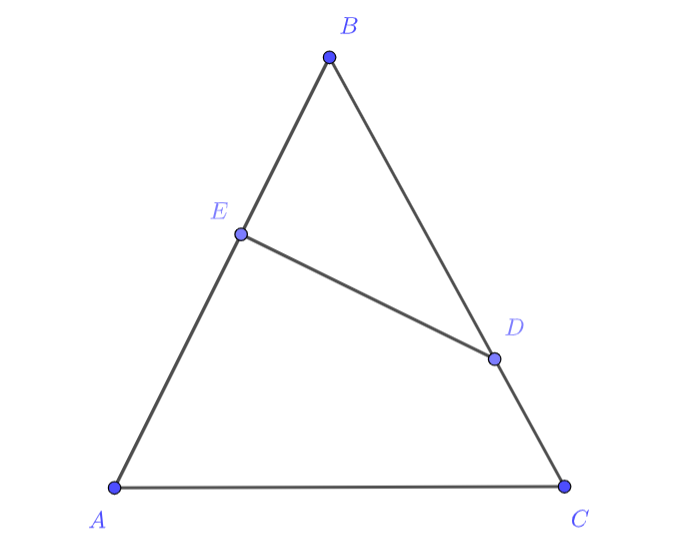
Пусть — проекция точки
на прямую
Так как
Следовательно, и
Имеем
(можно использовать
). Тогда
и
— расстояние от точки
до прямой
Далее, по теореме косинусов из
получаем
Следовательно, радиус окружности, описанной около треугольника равен



