Тема ДВИ по математике в МГУ

Стереометрия на ДВИ

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела дви по математике в мгу

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#91958

Плоскость $π$ перпендикулярна ребру $SA$ правильной треугольной пирамиды $ABCS$ с вершиной $S$ и основанием $ABC$ , делит это ребро в отношении $1:2$ (считая от вершины $S$ ) и проходит через середину ребра $SB$ . Найдите угол между плоскостью $π$ и плоскостью основания пирамиды.

Источники: ДВИ - 2024, вариант 241, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте построим сечение MNK (M∈AS, N∈SB, K∈SC) пирамиды SABC плоскостью π. Обозначим AS = 6х и попробуем выразить все отрезки на рисунке через х (для этого можно воспользоваться теоремой косинусов для треугольника △ASB, ведь cos∠ASB мы можем без проблем найти, так как на рисунке есть очень много прямоугольных треугольников)

Подсказка 2

Проведём LN — среднюю линию треугольника △ASB, обозначим за Р середину NK. Какой угол требуется найти в задаче?

Подсказка 3

Конечно, угол ∠MPL! Так как мы уже знаем соотношение практически всех отрезков, мы можем без труда найти значение синуса этого угла)

Показать ответ и решение

Первое решение.

Пусть $π$ пересекает $AS,$ $BS$ и $CS$ в точках $P,$ $R$ и $Q$ соответственно (то есть $π = (PQR )).$ Тогда по условию $SR = RB$ и $AP = 2PS.$ Пусть $M$ — середина $BC.$ Тогда пирамида $SABC$ симметрична относительно плоскости $(SAM ).$ Поскольку $π$ пересекает ребро $SB$ в середине, то в силу симметрии эта плоскость пересекает $CS$ тоже в середине, поэтому $QC = QS.$

$PIC$

Пусть $K$ — середина $AP.$ Тогда $PS =P K = AK,$ так как $AP = 2P S.$ Тогда, поскольку $SP :PK = SR :RB,$ то $PR$ и $KB$ параллельны. Аналогично можно доказать, что $RQ$ и $BC$ параллельны. Таким образом, $π$ и $(KBC )$ — параллельные плоскости, поэтому требуемый в задаче угол равен углу между $(KBC )$ и $(ABC ).$

Так как по условию $π$ и $AS$ перпендикулярны, то $(KBC )$ и $AS$ перпендикулярны, то есть $BK$ и $CK$ перпендикулярны $AS.$ Снова применив соображение симметрии, получаем, что $KB = KC,$ то есть $△KBC$ — равнобедренный, и $KM$ — его высота, поскольку $M$ является серединой $BC.$ Так как $ABC$ — правильный треугольник (по условию $SABC$ — правильная пирамида), то $AM$ — тоже высота в треугольнике $ABC.$ Таким образом, $KM$ лежит в плоскости $(KBC )$ и перпендикулярно $BC,$ а $AM$ лежит в плоскости $ABC$ и перпендикулярно $BC.$ Эти плоскости пересекаются по прямой $BC.$ Таким образом, нужный угол по определению равен $∠KMA.$

Пусть $AB = BC = AC = 2a.$ Тогда $BM =MC =a,$ так как $M$ — середина $BC.$ По теореме Пифагора из треугольника $ABM$ получаем $AM = √3a.$ По теореме Пифагора из треугольника $KSB$ получаем $KB2 = 5x2.$ С другой стороны, по теореме Пифагора из треугольника $AKB$ имеем $KB2 = 4a2− x2.$ Таким образом, $4a2 − x2 = 5x2,$ то есть $∘ -- x = 23a.$

Так как $KBC$ и $AS$ перпендикулярны, то $KM$ и $AS$ перпендикулярны. Из прямоугольного треугольника $AKM :$

∘ -- x 2a √2- sin ∠AMK = √3a-= √33a-= -3-

Таким образом, $√- ∠AMK = arcsin-23 .$

______________________________________________________________________________________________________________________________________________________

Второе решение.

Пусть $π$ пересекает $AS$ в точке $H,$ $BS$ — в точке $M.$ Пусть $AS = CS =BS = 6x.$ Тогда из условия следует, что $SH =2x,$ $AH = 4x,$ так как $SH :AH = 1:2.$ $M$ — середина $SB,$ поэтому $SM = SB =3x.$

$PIC$

По теореме Менелая для треугольника $ASC$ и прямой $HT :$

4x 3x CT- 2x ⋅3x ⋅TA = 1

Таким образом, $TA =2CT,$ поэтому $AC = CT.$ Пусть $AC = y.$ По теореме Менелая для треугольника $AHT$ и прямой $SC :$

y TM 2x y ⋅MH--⋅6x = 1

Таким образом, $TM = 3MH.$ Так как $AS$ по условию является перпендикуляром к плоскости $π,$ то $T H$ и $AS$ перпендикулярны. Тогда по теореме Пифагора из треугольника $SMH$ получаем $√- HM = 5x.$ То есть $√- TM = 3 5x.$ По теореме Пифагора для треугольника $AHT :$

16x2 +80x2 = 4y2

Таким образом, $√- y = 2 6x.$ Пусть $O$ — основание высоты пирамиды $SABC.$ Углы между плоскостями равны углам между перпендикулярами к ним, поэтому

∠(π,(ABC )) =∠(SA,OS)

Из прямоугольного треугольника $ASO$ получаем $sin∠ASO = AAOS-.$ Так как $O$ — точка пересечения медиан правильного треугольника $ABC,$ то $√- √- AO = -33 y = 2 2x.$ Тогда

√- √- sin∠ASO = AO-= 2-2x = -2- AS 6x 3

Таким образом, $∠ASO = arcsin√2. 3$

______________________________________________________________________________________________________________________________________________________

Третье решение.

Пусть искомый угол это $φ.$ Обозначим пересечение плоскости $π$ с ребрами $SA, SB, SC$ точками $M, N, K$ соответственно. $N$ — середина ребра $SB,$ следовательно, $K$ тоже середина ребра, так как пирамида правильная. По условию $NM ⊥ SA, KM ⊥ SA.$ Обозначим длину $SA$ как $6x,$ тогда получаем, что

SM = 2x, AM = 4x, SN = NB = SK =KC =3x

$PIC$

В треугольнике $MSN :$

2x 2 cos∠MSN = 3x = 3

Тогда по теореме косинусов для треугольника $ASB$ получаем

2 2 2 2 2 2 2 AB = AS + SB − 2⋅AS⋅SB ⋅cos∠MSN = (6x) +(6x) − 2⋅6x⋅6x⋅3 =24x

√- AB = 2x 6

Обозначим середину ребра $SA$ точкой $L.$ Тогда треугольник $LNK$ правильный, так как треугольник $ABC$ правильный, а также плоскость $(LNK )$ параллельна плоскости основания. $LN$ — средняя линия в треугольнике $ASB,$ следовательно, $LN =x√6.$ Обозначим точкой $P$ середину $NK.$ В треугольнике $LNK :$

LN √3 3x√2- LP = --2-- =--2-

так как треугольник $LNK$ правильный.

Так как плоскость $(LNK )$ параллельна плоскости основания, то найдем угол между этой плоскости и плоскости $π.$

MP ⊥ NK, LP ⊥ NK =⇒ ∠LPM = φ

Так как $L$ — середина, то $LM =x.$ В прямоугольном треугольнике $LP M (MP ⊥SA )$ находим, что

LM x √2 sin∠LPM = -LP = 3x√2-= -3- 2

Тогда

√- ∠LMP = φ =arcsin -2- 3

Ответ:

$arcsin√2 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#91981

В основании пирамиды лежит трапеция $ABCD, AD∥BC,AD = 2BC$ . Сфера радиуса 1 касается плоскости основания пирамиды и плоскостей её боковых граней $ADS$ и $BCS$ . Найдите отношение, в котором делит объём пирамиды плоскость $ADT$ , где $T$ - точка касания сферы с плоскостью $BCS$ , если грань $ADS$ перпендикулярна плоскости основания, а высота пирамиды равна 4.

Источники: ДВИ - 2024, вариант 242, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Так как сфера касается трех граней, сразу обозначим, что она касается плоскости ADS в точке R, а плоскости ABCD в точке P, O — центр сферы. Что можно сказать про точки T, P, R? Хотелось бы нарисовать рисунок как можно аккуратнее, как тогда удобнее всего было бы работать с перпендикулярностью грани и основания и высотой в этой грани?

Показать ответ и решение

Так как плоскость $(ADS )$ перпендикулярна $(ABC ),$ высота $SH$ пирамиды $SABCD$ лежит в грани $ADS.$ Без ограничения общности можно считать, что сфера касается плоскости $(ADS)$ в точке $R,$ лежащей на высоте $SH$ (этого можно добиться, если выполнять перенос сферы параллельно плоскости основания пирамиды).

Пусть сфера касается плоскости $(ABC )$ в точке $P.$ Докажем, что точки $T,$ $P$ и $Q$ лежат в одной плоскости и эта плоскость содержит $SH$ . Пусть $O$ — центр сферы. $RH$ — перпендикуляр к плоскости $(ABC ),$ так как это отрезок на высоте пирамиды. $P$ — точка касания сферы и $(ABC ),$ поэтому $OP$ и $(ABC)$ перпендикулярны. Таким образом, $OP$ и $RH$ параллельны, поэтому $O,$ $P,$ $R,$ $H$ лежат в одной плоскости (тогда и $S$ лежит в этой плоскости). $BC || AD,$ так как эти отрезки являются основаниями трапеции $ABCD.$ Тогда плоскость $(SBC)$ параллельна прямой $AD.$ Докажем, что $AD ⊥ (SHP).$

Мы уже знаем, что $SH ⊥ AD.$ Теперь заметим, что все три угла $∠ORH,$ $∠RHP$ и $∠OPH$ — прямые, поэтому $ORHP$ — прямоугольник. Тогда $PH$ — перпендикуляр к плоскости $(ADS),$ так как $(ADS)$ и $(ABC)$ перпендикулярны. Таким образом, $P H ⊥ AD.$ Тогда, действительно, $AD ⊥ (SHP ).$ $OT ⊥(SBC )$ и $AD || (SBC ),$ поэтому $OT ⊥ AD.$ Точка $O$ лежит в плоскости $(SHP ).$ Эта плоскость перпендикулярна $AD,$ при этом $OT$ — прямая, перпендикулярная $AD.$ Тогда $OT$ тоже лежит в плоскости $(SHP ).$

Ранее мы отмечали, что $ORHP$ — прямоугольник. Так как $OP =OR$ — радиусы сферы, то на самом деле этот прямоугольник является квадратом. $SH = 4,$ тогда $SR = SH − RH = 3.$ $ST =SR = 3$ — отрезки касательных. Пусть плоскость $(SHP )$ пересекает $BC$ в точке $K.$

$PIC$

Пусть $KT =KP = c$ (эти отрезки действительно равны, как отрезки касательных). По теореме Пифагора для $△SHK :$

2 2 16+ (c+ 1) =(c+ 3)

Решаем это уравнение и получаем $c=2.$ Теперь через точку $T$ проведем прямую $NL,$ параллельную $BC,$ причем $N ∈ SB$ и $L ∈SC.$ Тогда $ANLD$ — это сечение пирамиды плоскостью $(ADT ).$ Действительно, плоскость $(ADT )$ пересекает $(SBC)$ по прямой, параллельной $(AD),$ при этом $AD || BC.$ Поэтому, действительно, линия пересечения $(ADT )$ и $(SBC )$ параллельна $BC,$ поэтому совпадает с $NL.$

Теперь по теореме Фалеса для углов $BST$ и $KSC$ получаем: $SN :NB =ST :TK = 3:2$ и аналогично $SL:LC = 3:2.$

Продлим $AB$ и $DC$ до пересечения в точке $Q.$

$PIC$

По условию $AD = 2BC,$ поэтому точки $B$ и $C$ соответственно середины $AQ$ и $DQ.$ Пусть $F = AN ∩ DL.$ Ясно, что $F ∈SQ.$ Применяем теорему Менелая к $△QSC$ и прямой $FD :$

QF-⋅ SL-⋅ CD-= 1 FS LC DQ

$CD-= 1, DQ 2$ $SL-= 3, LC 2$ поэтому $QF-= 4. FS 3$ Пусть $V$ — объем пирамиды $QADS.$ Пирамида $QADS$ имеет общую высоту $SH$ с нашей пирамидой $SABCD.$ Треугольники $QAD$ и $QBC$ подобны с коэффициентом $2,$ поэтому $SQAD = 4SQBC.$ Тогда получаем, что $SABCD = 3SQAD, 4$ причем $QAD$ — основание пирамиды $QADS,$ если принять $S$ за ее вершину. По формуле объема пирамиды:

1 1 3 3 1 3 VSABCD = 3 ⋅SABCD ⋅SH = 3SH ⋅4SQAD = 4(3 ⋅SH ⋅SQAD )= 4V

По теореме о пирамидах с общим трехгранным углом при вершине:

VSAFD SA SFSD SF 3 VSAQD-= SA-⋅SQSD-= SQ-= 7

Таким образом, $VSAFD = 37V.$ Снова по теореме о пирамидах с общим трехгранным углом при вершине:

VSNLF-= SN-⋅ SL-⋅ SF-= 3⋅ 3⋅ 3 = 27 VSBQC SB SC SQ 5 5 7 175

$V = V − V = 1V. SBQC SABCD 4$ Таким образом, $V = 27V. SNLF 700$ Тогда $V = V − V = 273V. SANLD SAFD SNLF 700$ $SANLD$ — одна из частей, на которые плоскость $(ADT )$ разбивает исходную пирамиду $SABCD.$ Объем второй части равен $3 273- 252- VNLABCD = VSABCD − VSANLD = 4V − 700V = 700V.$ Тогда требуемое по условию отношение равно

VNLABCD 252V 12 -VSANLD- = 720073V-= 13 700

Ответ: 12 : 13

Ошибка.
Попробуйте повторить позже

Задача 3#92118

В основании прямой призмы лежит ромб со стороной 3. Найдите объём призмы, если известно, что существует сфера радиуса 1, касающаяся плоскости нижнего основания, двух противоположных боковых рёбер и всех рёбер верхнего основания.

Источники: ДВИ - 2024, вариант 243, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Построим чертёж! Проведите перпендикуляры из центра сферы к параллельным между собой боковым рёбрам (в точки касания). Что можно сказать о фигуре, образованной диагональю ромба, частями этих рёбер и проведёнными перпендикулярами?

Подсказка 2

Теперь мы знаем диагональ ромба! Это позволяет нам полностью обсчитать ромб, найти его углы/высоту/площадь и всё что нам нужно!

Подсказка 3

Спроецируем радиус сферы, проведённый в точку касания её с ребром верхнего основания, на плоскость основания. Эта проекция — половина высоты ромба.

Подсказка 4

Работа с теоремой Пифагора поможет нам отыскать оставшуюся часть высоты призмы. Осталось подставить числа в формулу и записать ответ.

Показать ответ и решение

Пусть дана призма $ABCDA ′B′C′D′,$ $O$ — центр данной сферы, которая касается боковых рёбер $BB′$ и $DD ′$ в точках $K$ и $L.$

Заметим, что $′ OK ⊥ BB$ и $′ OL ⊥ DD ,$ следовательно $′ KL ⊥ BB .$ А раз $′ BB ⊥ BD$ и все четыре точки $B,K,L,D$ лежат в одной плоскости, то $KL ∥KL$ и $BKLD$ — прямоугольник, значит, $BD =KL,$ при этом $KL = 2$ как диаметр данной сферы.

Рассмотрим треугольник $ABD$ и найдём высоту $DH.$ По формуле Герона $√- SABD = 2 2,$ тогда

1 SABD = 2DH ⋅AB

√- 3DH = 2 2 2

√ - DH = 4-2 3

Проецируем $O$ на нижнее основание, обозначим проекцию на $Q,$ она будет являться серединой $BD.$ Пусть $G$ — точка касания сферы с $A′B ′,$ а $E$ — её проекция на нижнее основание.

$PIC$

Раз $OG ⊥A ′B′$ , то в силу ТТП и свойств проекции $QE ⊥ AB.$ Тогда $QE$ — средняя линия в треугольнике $BDH,$ следовательно $√ - QE = 1DH = 2--2. 2 3$

Рассмотрим прямоугольную трапецию $GOQE,$ в ней $OG =OQ = 1$ и $2√2 QE = -3-.$ Пусть $GE = h,$ тогда по теореме Пифагора

(GE − OQ)2+ QE2 = OG2

(h− 1)2 + 89 = 1

h = 4 3

Теперь зная это, посчитаем объём призмы

- - 4√2 4 16√2 V =SABCD ⋅GE = AB⋅DH ⋅GE = 3⋅ 3 ⋅3 = 3

Ответ:

$16√2 3$

Ошибка.
Попробуйте повторить позже

Задача 4#92263

Дан куб со стороной 1, основаниями $ABCD, A′B ′C′D′$ и боковыми рёбрами $AA ′,BB′,CC′$ и $DD′$ . На рёбрах $A′B′,B ′B,BC,CD, DD′,D′A′$ отмечены точки $K,L,M,N,O,P$ coответственно. Найдите отношение, в котором плоскость $KMO$ делит объём куба, если известно, что

′ ∠A AK = ∠LAK,∠BAM = ∠NAM, ∠DAO = ∠PAO

и что

′ ′ 5 A K+ LB = BM + ND = DO +PA = 4.

Подсказки к задаче

Подсказка 1

В условии нам дана сумма некоторых пар отрезков, быть может, тогда обозначим A’K за x и посчитаем остальные отрезки в грани ABB’A’? Также обратим внимание на то, что ребра в этой грани параллельны, так что можно использовать и подобие!

Подсказка 2

BL = 5/4 - x, LB’ = x - 1/4, а если провести AL до пересечения с A’B’ в точке T, то несложно выразить и B’T. А в составе какого отрезка лежит B’T? Давайте выразим его через больший треугольник!

Подсказка 3

B’T = A’T - 1, а A’T можно выразить через тангенс угла A! Теперь мы умеем выражать B’T двумя способами, чему тогда равен х?

Подсказка 4

x = 1/2! Супер, теперь мы знаем, что K — середина A’B’. Но ведь это верно не только для точки K…

Подсказка 5

Аналогично M — середина BC, O — середина DD’! Теперь мы видим, что сечение у нас достаточно красивое и даже симметричное ;) осталось понять, относительно чего…

Показать ответ и решение

Рассмотрим грань $AA ′B ′B$ . Пусть $A ′K = x,$ тогда $BL = 5− x, 4$ $LB′ = x− 1. 4$

$PIC$

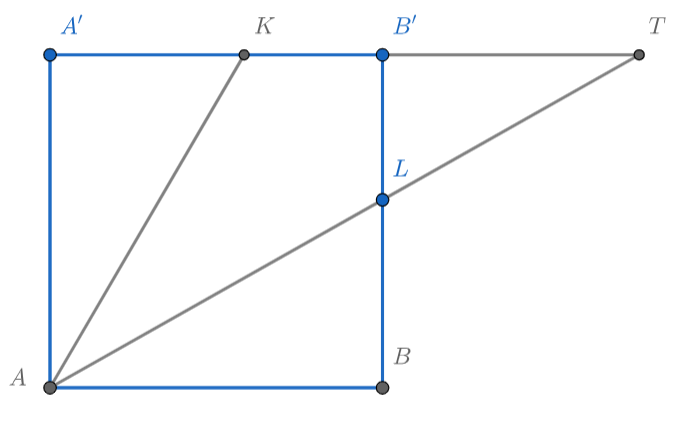
Продлим до пересечения лучи $AL$ и $A′K,$ точку пересечения назовём $T$ и выразим $B′T$ , используя подобие треугольников $ALB$ и $TLB ′ :$

B′T = x-− 14-= 4x−-1. 54 − x 5− 4x

Выразим теперь $′ B T$ вторым способом: через треугольник $′ AA T$ и тангенс $∠A :$

A′K tg∠A′AK = AA′-=x.

Используя формулу тангенса двойного угла, получаем, что

A′T = tg∠A ′AT = -2x-2. 1− x

Отсюда

′ ′ 2x−-1+-x2- 4x−-1 B T = A T − 1= 1− x2 = 5− 4x .

Отсюда можно найти $x$ : перемножая пропорцию и приводя подобные, получим квадратное уравнение $2 4x − 10x+ 4= 0$ , которое имеет решения $x =2$ и $1 x =2.$ По построению $x$ не может превосходить единицу, поэтому $1 x= 2,$ то есть $K$ — середина $′ ′ A B$ .

Аналогично получаем, что $M$ — середина $BC,$ и $O$ — середина $DD ′.$

$PIC$

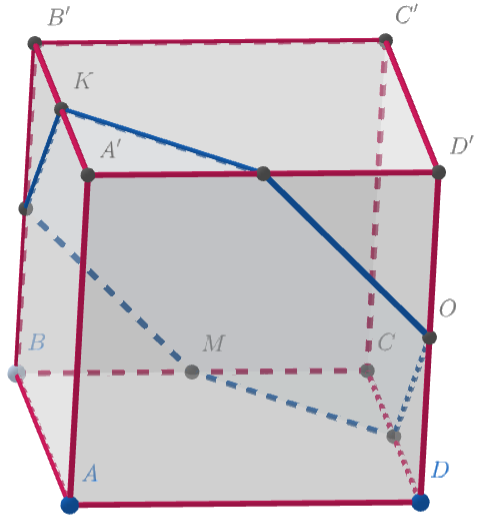
Заметим, что через $K,M,O$ проходит плоскость, которая высекает из данного куба шестиугольник и пересекает ещё три ребра в серединах: рёбра $A ′D ′,BB′$ и $CD$ . Такая плоскость часто встречается в задачах: явно построить сечение можно классическим способом, параллельными переносами отрезков. А если уже встречались с таким построением, можно показать, что все 6 точек действительно лежат в одной плоскости, используя параллельность диагоналям граней куба. Поскольку через три точки $K,M,O$ можно провести только одну плоскость, этот шестиугольник и будет сечением куба плоскостью $KMO.$

Сечение центрально симметрично относительно центра куба $I.$ Середины отрезков $CD$ и $B ′A′$ симметричны относительно центра, как и середины отрезков $A′D′$ и $BC,$ $DD ′$ и $B′B$ . Таким образом, имеем центральную симметрию всего построения относительно центра куба, следовательно, плоскость делит куб на две равные фигуры.

Ответ: 1 : 1

Ошибка.
Попробуйте повторить позже

Задача 5#92348

Все рёбра прямой треугольной призмы $ABCA ′B ′C′$ с основанием $ABC$ и боковыми ребрами $AA ′,$ $BB ′,$ $CC ′$ равны. Найдите отношение, в котором делит объем этой призмы плоскость, проходящая через вершину $′ C$ и через середины ребер $AB,$ $′ AA .$

Подсказки к задаче

Подсказка 1

Пусть M и N — середины AA’ и BB’ соответственно, секущая плоскость пересекает CB в точке K, а T — пересечение KN и TC’. Нам было бы очень полезно узнать, в каком соотношении K делит CB. Давайте тогда попробуем записать какие-нибудь подобия и отношения отрезков!

Показать ответ и решение

Пусть $M$ и $N$ — середины $AA′$ и $BB′$ соответственно. Пусть секущая плоскость пересекает отрезок $BC$ в точке $K$ и $′ C M ∩ KN = T$ (тогда наше сечение — это $′ KC MN$ ). Ясно, что $T$ лежит на прямой $AC.$ Пусть $AH$ — высота треугольника $ABC.$ Пусть $′ TH ⊥ BC,$ причем $′ H$ лежит на прямой $BC.$

$PIC$

$CC′$ и $AM$ параллельны, причем $AM = 12AA′ = 12CC ′,$ тогда треугольники $CC ′T$ и $AMT$ подобны с коэффициентом $2.$ Тогда $CT = 2AT.$ Треугольники $CAH$ и $TCH ′$ подобны с коэффициентом $2,$ так как $AH || TH ′$ и $TC = 2AC.$ Тогда $TH ′ =2AH.$ По теореме Менелая для треугольника $ABC$ и прямой $KN$ получаем

CK- ⋅ BN-⋅ AT-= 1 KB NA CT

Тогда получаем $CK-= 2, KB 1$ следовательно, $KB-= 1. BC 3$ Пусть $V =V ′′ ′. ABCA B C$ По формуле объема

′ 1 ′ V =SABCBB = 2AH ⋅BC ⋅BB

1 ′ 1 ′ 1 VABCC′ =3CC ⋅SABC = 6CC ⋅AH ⋅BC =3V

VCC′KT = VCC-′KT-⋅ V-= VCC′KT-V-= 4 V V∕3 3 VC′CBA 3 9

V = SANT-⋅ MA ⋅ V-= VAN-⋅AT-⋅sin∠NAT MNTA SABC AA′ 3 6CB ⋅CA ⋅sin∠CAB

Так как $∘ ∠CAB + ∠NAT = 180,$ то $sin∠CAB = sin∠NAT.$ Тогда $-V VMNTA = 12.$

Выразим объем фигуры $′ MC ANKC$ — одной из частей, на которые разделила призму секущая плоскость:

4 1 13 VMC ′ANKC =VCC′KT − VMNTA = 9V − 12V =36V

Тогда $VBKNA ′B′C′ = V − VMC ′ANKC = 2336V.$ Тогда получаем

23 VBKNA′B′C-′= 36V-= 23- VMC ′ANKC 1336V 13

Ответ: 13 : 23

Ошибка.
Попробуйте повторить позже

Задача 6#92367

Расстояние от середины высоты правильной четырёхугольной пирамиды до боковой грани равно $√2-$ , а до бокового ребра — $√3$ . Найдите объём пирамиды.

Показать ответ и решение

Пусть нам дана правильная четырехугольная пирамида $SABCD$ с основанием $ABCD.$ Пусть $O$ — основание высоты этой пирамиды. Заметим, что расстояние от $O$ до плоскости $BSC$ равно удвоенному расстоянию от середины высоты до этой плоскости. Аналогично с расстоянием до бокового ребра $AS.$ Пусть $OQ$ — перпендикуляр к $AS,$ а $OP$ — перпендикуляр к апофеме $SH$ плоскости $BSC.$

$PIC$

Так как $H$ — середина $BC,$ то $BC ⊥OH.$ А также поскольку $SO$ — высота, то $BC ⊥ OS.$ Тогда $BC$ перпендикулярна $SOH,$ в частности, перпендикулярна и к $OP.$ Тогда получается, что $OP$ перпендикулярна к $SH,BC,$ а значит, $OP = 2√2$ как расстояние от основания высоты до боковой грани.

Положим, что $OH = x,$ тогда $AO = x√2$ так как в квадрате диагональ в $√2$ раз длиннее стороны. Теперь запишем отношения площадей прямоугольных треугольников $ASO$ и $SOH :$

- -SASO- -AO √ - AS-⋅OQ- AS-⋅2√-3 SSOH = OH = 2= SH ⋅OP = SH ⋅2√ 2

AS 2 SH-= √3-

Теперь пусть $AS =2a,$ тогда $√- SH =a 3.$ А из прямоугольного треугольника $SHC$ по теореме Пифагора $HC = a= OH = x.$ Теперь же из треугольника $SOH$ по теореме Пифагора:

OS = x√2

Тогда по формуле высоты для этого же треугольника:

√ - 2√2 = x-√2⋅x x 3

√ - x = 2 3

Наконец, по формуле объема пирамиды:

VSABCD = 1x⋅4x2 = 32√6. 3

Ответ:

$32√6$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#89780

Ребро основания правильной треугольной пирамиды равно $√6$ , высота пирамиды равна $√7-$ . Плоскость $π$ перпендикулярна одному из рёбер пирамиды и делит его в отношении $1:2$ , считая от вершины. Найдите отношение, в котором плоскость $π$ делит объём пирамиды.

Источники: ДВИ - 2023, вариант 237, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть SABC — данная пирамида, плоскость π будем строить перпендикулярно ребру SA. Что можно сказать о рёбрах SA и BC? Какой вывод из этого можно сделать относительно π и ВС?

Подсказка 2

π || BC, что тогда можно сказать о пересечении плоскостей π и (SBC)? Достройте сечение, пользуясь тем, что SA ⊥ π, а значит и любой прямой, находящейся в этой плоскости

Подсказка 3

Чтобы найти отношение объёмов исходной пирамиды и пирамиды, отсечённой плоскостью π, удобно взять за основание треугольники △BSC и треугольник, отсекаемый плоскостью π при пересечении с гранью SBC.

Показать ответ и решение

Обозначим через $A,B,C,S$ вершины пирамиды, так что $ABC$ — ее основание, а плоскость $π$ перпендикулярна ребру $SA$ .

Поскольку $π ⊥ SA$ и $BC ⊥ SA$ , имеем $π ∥ BC$ . Стало быть, $π$ пересекает плоскость $BCS$ по прямой, параллельной $BC$ , и делит ребра $SB$ и $SC$ (или их продолжения) в одинаковом отношении. Найдем это отношение.

Обозначим через $H$ основание высоты пирамиды и через $M$ — середину ребра $BC$ . Тогда

AB√3- 3√- AM = --2--= 2 2;

AH = 2AM = √2. 3

Пусть $K$ — точка пересечения $π$ и $SA,L$ — точка пересечения $π$ с прямой $AM, N$ — точка пересечения прямых $LK$ и $SM$ . Тогда $AK = 2KS$ , причем $∠AKL =90∘.$

$PIC$

Из подобия треугольников $ALK$ и $ASH$ получаем:

2√---2----2 √---A2H----2 = 3-AH-+-SH-, AH + SH AL

откуда

2 AL = 3(2√+-7)-=3√2-= 2AM. 2

Итак, $M$ — середина $AL$ . Обозначим через $P$ середину $AK$ . Тогда $LK∥MP$ , откуда $SN =$ $NM$ , ибо $SK = KP$ .

Таким образом, плоскость $π$ проходит через середины ребер $SB$ и $SC$ . Следовательно, $π$ отсекает от пирамиды $ABCS$ пирамиду, объем которой равен

1 1 1 VABCS 3 ⋅2 ⋅2 ⋅VABCS =-12-

То есть $π$ делит объем исходной пирамиды в отношении $1 :11.$

Ответ: 1 : 11

Ошибка.
Попробуйте повторить позже

Задача 8#90508

Дан куб с ребром 1, нижним основанием $ABCD$ и боковыми ребрами $AA ,BB ,CC ,DD 1 1 1 1$ . На ребрах $A D ,BB ,CC ,AD 1 1 1 1$ отмечены соответственно точки $K,L,M,N$ , так что $A1K =KD1$ , $BL :LB1 = 7:1$ , $CM :MC1 = DN :NA = 4:3$ . Найдите площадь сечения тетраэдра $KLMN$ , параллельного ребрам $KL$ и $MN$ , имеющего форму ромба.

Источники: ДВИ - 2023, вариант 236, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Начнём с хорошего чертежа! Возможно, будет удобно отдельно вынести тетраэдр KLMN, чтобы удобнее было работать с сечением. В каком случае сечение тетраэдра будет ромбом? А что нам нужно, чтобы найти его площадь?

Подсказка 2

Будем вычислять стороны ромба и угол между ними. Заметим также, что этот угол равен углу между рёбрами KL и MN тетраэдра. Итак, пусть вершина ромба делит ребро KN в отношении х/у, что можно сказать о том, в каких отношениях вершины ромба делят другие рёбра тетраэдра? Параллельность нам поможет это установить!

Подсказка 3

При помощи теоремы Пифагора можно вычислить любое ребро тетраэдра. А подобие треугольников поможет нам после этого отыскать сторону ромба. Но как же найти угол?

Подсказка 4

KL и MN, а также другие пары параллельных им прямых, не выглядят удобными для построения угла между прямыми напрямую, однако куб — очень хорошая фигура для работы с декартовой системой координат! Введите координаты и при помощи работы с векторами определите искомый угол. Остаётся лишь подставить найденные значения в формулу площади ромба и задача убита!

Показать ответ и решение

Пусть $c$ — длина стороны ромба, $α$ — его меньший угол. Тогда искомая площадь равна $c2sinα,$ причем угол $α$ равен углу между прямыми $KL$ и $MN,$ т.к. сечение параллельно ребрам $KL$ и $MN.$

$PIC$

Найдем $c.$ Пусть сечение пересекает стороны $KN,LN,LM, KM$ в точках $H,I,J,O$ соответственно. Тогда $HI ∥ KL$ и $IJ ∥NM.$ Пусть $KH$ и $HN$ имеют длину $x$ и $y$ соответственно. По теореме о пропорциональных отрезках для параллельных прямых $HI$ и $KL$ понимаем, что

LI-= KH-= x IN HN y

Из подобия треугольников $NHI$ и $NKL$ и треугольников $LIJ$ и $LNM$ получаем

-x-- -y-- c= x+ yNM = x+yKL

Отсюда $KL x= y⋅NM-,$ то есть

1 c= -1-+--1- KL NM

По теореме Пифагора

∘ ---1---1- 9 ∘ ---16---16 9 KL = 1+ 4 + 64 = 8, NM = 1+ 49-+ 49 = 7,

Отсюда $3 c= 5.$

Найдем угол $α$ — угол между $KL$ и $MN.$ Он равен углу между направляющими для этих прямых векторами $( ) 12,1,18$ и $( ) − 47,1,− 47 .$ Их скалярное произведение равно $( ) 1− 12 + 18 ⋅ 47 = 914.$ Следовательно,

cosα= -9 ⋅ 8⋅ 7 = 4 14 9 9 9

Соответственно,

√-- sinα = -65 9

Значит, искомая площадь равна

( 3)2 √65 √13 5 ⋅ 9 = 5√5-

Ответ:

$√13 5√5-$

Ошибка.
Попробуйте повторить позже

Задача 9#90509

Найдите объём правильной четырёхугольной пирамиды со стороной основания равной 1, если известно, что плоские углы при вершине равны углам наклона боковых рёбер к плоскости основания.

Источники: ДВИ - 2023, вариант 233, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть пирамида — SABCD и её высота — SН. Плоский угол при вершине назовём α. SA = x. Отметьте равные углы и давайте двумя способами найдём cos(α): по теореме косинусов из △SAD и как отношение АН/SA

Подсказка 2

Решение квадратного уравнения поможет нам вычислить х. Какой из корней получился посторонним?

Подсказка 3

ОТТ поможет нам найти sin(α) и затем, с его помощью, высоту. Осталось лишь внимательно поработать с некрасивыми числами и записать ответ!

Показать ответ и решение

Пусть $SABCD$ — данная правильная четырехугольная пирамида с вершиной $S$ и высотой $SH, AB = 1.$ Обозначим $∠BSC = ∠SCH = ∠α.$

$PIC$

Из прямоугольного треугольника $CSH$ находим, что

1√- SC = --CH----= --2-= √-1--- cos∠SCH cosα 2cosα

Пусть $M$ — середина ребра $BC.$ Из прямоугольного треугольника $CSM$ находим, что

--CM---- --12--- --1---- SC = sin∠CSM = sin(α2) = 2sin(α2)

Значит,

( ) √-1---= --1-α =⇒ √2sin α-= cosα 2cosα 2sin 2 2

2(α) 2 2 sin 2 = cosα

2 2 1− cosα =cos α =⇒ cos α+ cosα− 1= 0 =⇒

√5−-1 cosα = 2

Тогда

∘-------- ∘ ---√----- ∘ ---√-- tg α= -1---− 1= 3+--5− 1= 1+--5 cos2α 2 2

√- ∘---√-- ∘ ----- SH = CH ⋅tgα= -2-⋅ 1-+--5= 1 1+√ 5 2 2 2

Следовательно,

∘ ----- ∘ --√-- VSABCD = 1SABCD ⋅SH = 1⋅1⋅ 1 1+√5-= --1+--5 3 3 2 6

Ответ:

$√1+-√5 6$

Ошибка.
Попробуйте повторить позже

Задача 10#90510

Пересечение плоскости и правильной треугольной пирамиды является квадратом со стороной 1. Найдите длину ребра основания пирамиды, если известно, что двугранный угол между плоскостью боковой грани и плоскостью основания равен $√1 arccos 3.$

Источники: ДВИ - 2023, вариант 238, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть исходная пирамида — SABC, SA = b. AB = a. Знание о том, что пирамида правильная, помогает нам понять, куда упадёт высота этой пирамиды, а значит — построить косинус двугранного угла. В каком случае сечение будет квадратом, как связаны его стороны с рёбрами пирамиды?

Подсказка 2

Выразите через а и b все отрезки, необходимые для нахождения косинуса, после этого можно будет установить связь между a и b. А как нам определить отношение стороны квадрата к ребру а?

Подсказка 3

Пусть вершина квадрата-сечения делит ребро АВ в отношении m/n, в каком отношении делится ребро SB этим же сечением? При помощи подобия треугольников и известного отношения a/b установите численно отношение m/n. После этого, подстановкой известных отношений, вычислите а.

Показать ответ и решение

Поскольку сечение — четырёхугольник, плоскость пересекает все грани. Обозначим вершшины основания через $A,B,C$ и вершину пирамиды через $D$ . Тогда можно считать, что секущая плоскость пересекает рёбра $AB,BD, DC,CA$ в точках $K,L,M,N$ соответственно. Поскольку $KL∥MN$ , прямая $KL$ параллельна всей плоскости $ADC$ . Стало быть, $MN ∥KL ∥AD$ . Аналогично, $KN ∥BC∥LM$ . Положим $a =AB,b =AD$ .

$PIC$

Тогда косинус двугранного угла при основании равен

∘-2a√3---= ∘-----1------, b2− a2 ( (b)2 ) 4 3 4 a − 1

что по условию равно $1√3$ , откуда $ba = √12$ . Из того, что $KL∥AD,LM ∥BC$ получаем:

-1= LM-= DL- = DB-− LB-= 1− LB-= 1− KL-= 1− 1. a BC DB DB DB AD b

Таким образом,

√ - 1 =1− --2, a a

то есть $√- a =1+ 2$ .

Ответ:

$a =1+ √2$

Ошибка.
Попробуйте повторить позже

Задача 11#64684

Высота правильной треугольной призмы $ABCA ′B′C′$ с основанием $ABC$ и боковыми рёбрами $AA ′,BB ′,CC′$ равна $1.$ Найдите длину ребра основания, если известно, что $′ ′ AB ⊥ BC .$

Источники: ДВИ - 2022, вариант 223, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Как мы можем применить данную нам перпендикулярность? Кажется, будет удобно построить из точки B' прямую B'B₁, параллельную BC' и взглянуть, на полученную конструкцию. Обозначьте неизвестную сторону основания какой-нибудь переменной и попробуйте выразить всё что тут можно!

Подсказка 2

В основании правильный треугольник, значит у нас есть угол в 60°. Имея в треугольнике две стороны и угол мы сумеем выразить третью сторону: отрезок, соединяющий А с точкой пересечения B'B₁ и плоскости основания. Эту же сторону мы можем выразить при помощи т. Пифагора.

Подсказка 3

Осталось только решить квадратное уравнение, отсечь лишний корень (сторона ведь не может быть отрицательной!) и задача повержена!

Показать ответ и решение

$PIC$

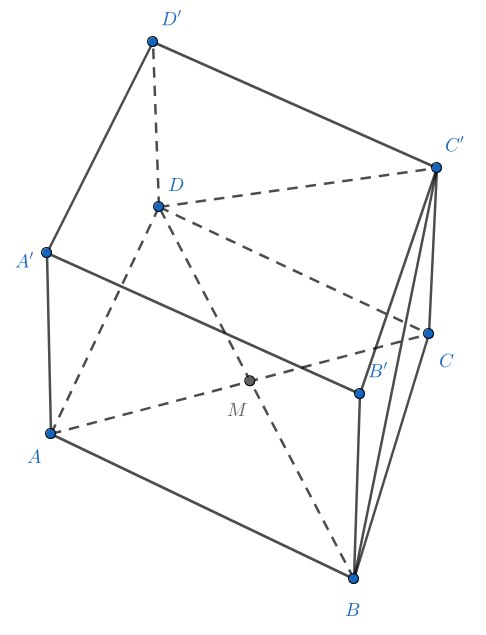
Достроим основания призмы $ABC, A′B ′C ′$ до параллелограммов, получим $ABCD,A ′B′C′D′$ . Получится параллелепипед, в котором $AB ∥DC, AB =CD$ и $AB ′ ∥DC′,AB′ = DC′$ , отсюда $DC′ ⊥ BC ′$ . Кроме того, $BC′ = DC′$ (призма правильная, можно воспользоваться симметрией. Отсюда $△BC ′D$ прямоугольный и равнобедренный. Если $AC ∩ BD = M$ , то $C ′M$ будет высотой этого треугольника, если дополнительно $AB = a$ , то $√- C′M =DM =BM = -32a,CM = AM = a2$ (используем свойства правильного треугольника). Из условия $CC ′ =1$ , применяя теорему Пифагора: $- C′C2+ CM2 = C′M2 ⇐ ⇒ 1+ a2∕4= 3a2∕4 ⇐⇒ a= √2$ .

Ответ:

$√2$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#64685

Дана правильная треугольная пирамида $ABCS$ с основанием $ABC$ и вершиной $S.$ Плоскость $π$ перпендикулярна ребру $AS$ и пересекает рёбра $AS,BS$ в точках $D,E$ соответственно. Известно, что $SD = AD$ и $SE = 2BE.$ Найдите косинус угла между ребром $AS$ и плоскостью основания $ABC.$

Источники: ДВИ - 2022, вариант 225, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пирамида правильная, поэтому мы чётко знаем куда падает её высота и искомый косинус будет легко выражаться, как только мы узнаем отношение её бокового ребра к ребру основания. Плоскость π перпендикулярна AS. Что в таком случае можно сказать о прямой DE пересечения этой плоскости с плоскостью (SAB)?

Подсказка 2

Итак, DE ⊥ AS. Тогда мы можем, зная положения точек D и E выразить косинус угла при вершине S. Рассмотрите теперь равнобедренный треугольник-грань △ASB: теорема косинусов поможет нам связать его боковые стороны со стороной основания.

Подсказка 3

Пирамида правильная, значит её высота падает в центр основания. Воспользуйтесь свойствами правильного треугольника и найденным в предыдущем пункте соотношением, чтобы выразить искомый косинус.

Показать ответ и решение

$PIC$

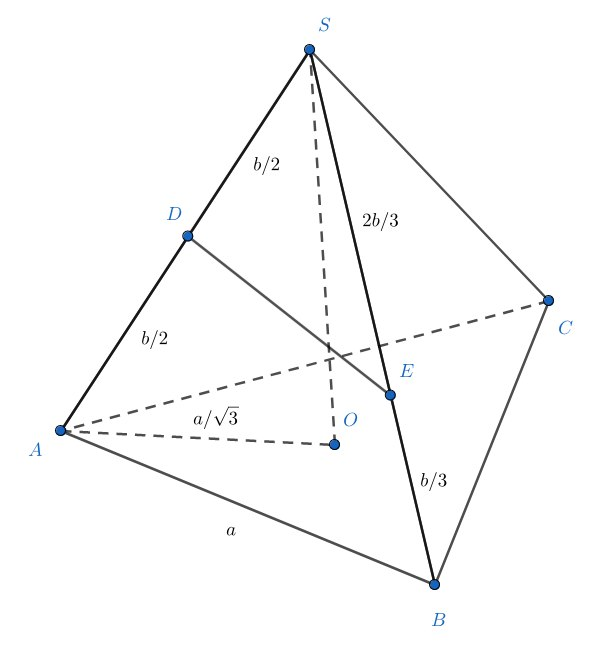
Пусть $a$ — длина ребра основания и $b$ — длина бокового ребра. В прямоугольном треугольнике $SDE$ имеем $SD = 12b$ и $SE = 23b$ . Стало быть, $cos∠ASB = 34$ . Применяя теорему косинусов к треугольнику $ASB$ , получаем, что $a2 =2b2− 2b2⋅ 34$ , откуда $√- b= a 2$ . Пусть $O$ — центр основания. Тогда в прямоугольном треугольнике $ASO$ имеем $√ - AS = b=a 2$ и $√- AO =a∕ 3$ . Стало быть, $√- cos∠SAO = AO∕AS =1∕ 6$ .

Ответ:

$√1- 6$

Ошибка.
Попробуйте повторить позже

Задача 13#64686

Дан куб $ABCDA ′B′C′D ′.$ Через середины его ребер $AA′,C′D ′$ и через центр грани $BCC ′B′$ проведена плоскость, пересекающая диагональ $′ DB$ куба в точке $O$ . Найдите отношение $DO$ : $′ OB .$

Источники: Вместо ЕГЭ - 2022, вариант ЕМ222, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Построение этого сечения не выглядит тривиальной задачей. Разберёмся для начала, какие точки этой плоскости нам нужны, чтобы отыскать искомое соотношение. Удобно будет работать с пересечением этой плоскости (назовем ее π) и диагональной (BDD'). Значит нам точно понадобится пересечение π c рёбрами BB' и DD'.

Подсказка 2

Можно заметить, что середина ребра C'D' и центр грани BCC'B' лежат в плоскости диагонального сечения (ABC'). Рассмотрите эту плоскость и поработайте с подобными треугольниками, чтобы определить точку пересечения плоскости π с прямой АВ — зная её, мы сможем посчитать и положение точки пересечения π с ребром BB'.

Подсказка 3

Определить точку пересечения π и DD' тоже не получится в один шаг: удобно это сделать сначала рассматривая всё ту же плоскость (ABC') и прямую AD' в ней. А потом можно будет высчитать и положение точки на DD'.

Подсказка 4

Осталось рассмотреть плоскость (BDD') и имеющуюся у нас теперь прямую её пересечения с π. Поработайте с подобными треугольниками, чтобы отыскать то самое соотношение DO:OB'

Показать ответ и решение

$PIC$

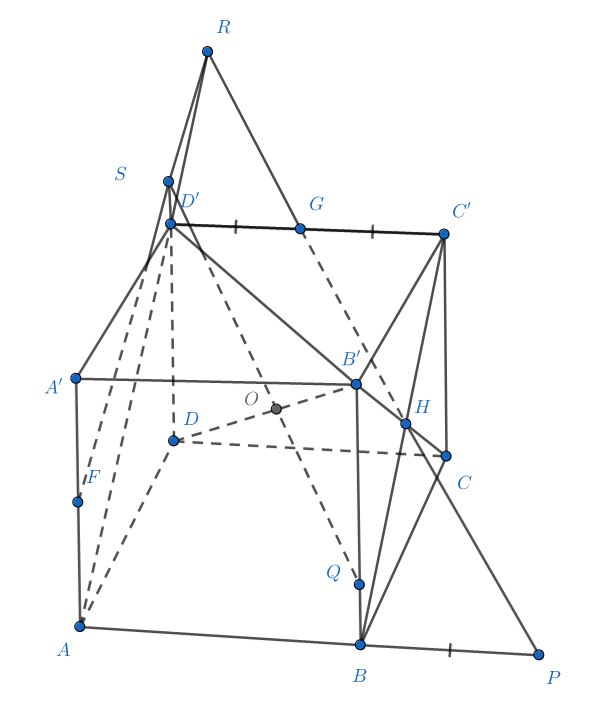
Обозначим середины ребер $AA′,C′D ′$ и центр грани $BCC ′B′$ через $F,G,H$ , соответственно. Обозначим также через $π$ плоскость $FGH$ .

Найдем точку $Q$ пересечения плоскости $π$ и прямой $BB′$ . Точки $G,H,A,B$ лежат в плоскости $ABC ′$ , следовательно прямые $GH$ и $AB$ пересекаются. Пусть $P$ - точка их пересечения. Тогда $BP = C′G= 12AB$ , поскольку треугольники $HC′G$ и $HBP$ равны. Точки $P$ и $F$ принадлежат $π$ , следовательно, прямая $FP$ есть прямая пересечения плоскости $ABB ′$ с $π$ . То есть $Q$ лежит на отрезке $BB ′$ . Из подобия треугольников $APF$ и $BPQ$ следует, что $BQ = 13AF = 16BB ′$ . Следовательно, $QB ′ = 56BB′$ .

Найдем теперь точку $S$ пересечения плоскости $π$ и прямой $DD ′$ . Прямая $GH$ лежит в плоскости $ABC ′$ , равно как и прямая $AD′$ . Обозначим через $R$ точку пересечения этих прямых. Из подобия треугольников $RAP$ и $RD ′G$ следует, что $RD ′ = 13RA$ . Точки $R$ и $F$ принадлежат $π$ , следовательно, прямая $F R$ есть прямая пересечения плоскости $ADD ′$ с $π$ . То есть $S$ лежит на продолжении отрезка $DD ′$ за точку $D ′$ . Из подобия треугольников $ARF$ и $D′RS$ следует, что $D′S = 1AF = 1DD ′ 3 6$ . Следовательно, $SD = 7DD ′ 6$ .

Прямая $SQ$ есть прямая пересечения плоскости $DBB ′$ с $π$ , то есть она проходит через $O$ . Треугольники $SDO$ и $QB′O$ подобны с коэффициентом подобия $7 5$ . Следовательно, $DO :OB′ =$ $7:5$ .

Ответ:

$7 5$

Ошибка.
Попробуйте повторить позже

Задача 14#90137

Объём треугольной призмы $ABCA ′B′C′$ с основанием $ABC$ и боковыми рёбрами $AA′,BB ′$ , $CC ′$ равен 72. Найдите объём тетраэдра $DEF G$ , где $D$ — центр грани $′ ′ ABB A,E$ — точка пересечения медиан треугольника $′ ′ ′ A BC ,F$ — середина ребра $AC$ и $G$ — середина ребра $BC.$

Источники: ДВИ - 2022, вариант 221, задача 4 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Лежащих в одной или хотя бы в параллельных плоскостях, оснований у призмы и тетраэдра не видно. Значит попробуем достроить удобную для вычисления фигуру, с помощью которой можно найти искомый объём через отношение.

Подсказка 2

Продлим ED до пересечения с плоскостью АВС, назовём I полученную точку. Как связаны объёмы тетраэдров IEFG и DEFG?

Подсказка 3

Связать объём тетраэдра IEFG с объёмом призмы можно взяв за основание тетраэдра △IFG: как его сторона FG и высота к этой стороне связаны с высотой и сторонами △АВС? Осталось аккуратно записать все найденные отношения и мы получим ответ!

Показать ответ и решение

Пусть $C′H$ и $CJ$ — медианы верхней и нижней грани, тогда $D$ лежит на $HJ$ — в центре средней линии параллелограмма. Отсюда следует, что при отражении $E$ относительно $D$ мы попадём на $CJ$ — в точку $I$ , то есть $VDEFG =VEFGI∕2$ .

$PIC$

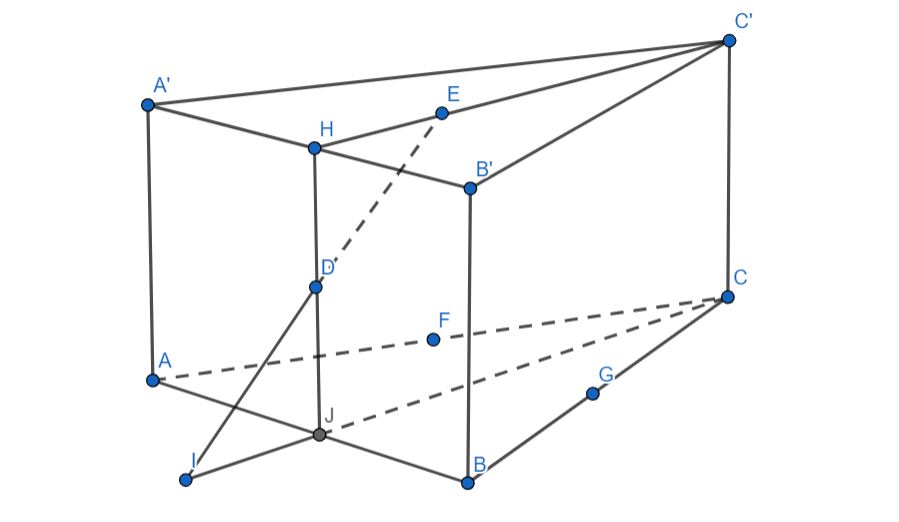
Также в силу симметрии $JI = HE = EC∕2$ ( $E$ — точка пересечения медиан), тогда $CI = 2⋅EC = 4∕3 ⋅CJ$ , однако заметим, что $FG$ делит $CJ$ пополам, то есть делит $CI$ в отношении $3 :5$ от вершины $C$ , откуда

SIFG = 5∕3⋅SCFG = 5∕12 ⋅SABC,

при этом высота совпадает с высотой призмы, откуда

VDEFG = VEFGI∕2= 5∕24⋅1∕3⋅SABC ⋅h =5,

где $h$ — та самая высота.

Ответ: 5

Ошибка.
Попробуйте повторить позже

Задача 15#63815

Дан тетраэдр $ABCD$ . Известно, что центр сферы, описанной около этого тетраэдра, лежит на $AB$ , что плоскости $ABC$ и $ABD$ перпендикулярны и что $AD =DC = CB$ . Найдите угол между прямыми $AD$ и $CB.$

Источники: ДВИ - 2021, вариант 214, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть К — центр описанной сферы. Отметьте равные отрезки-радиусы сферы. Какой вывод можно сделать, смотря на △ADB и его медиану, равную половине стороны? Какой вывод можно сделать о △АВС?

Подсказка 2

Итак, перед нами два прямоугольных треугольника с общей гипотенузой и равными катетами, значит они сами...? Проведите высоту DH в △ADB, что можно сказать об отрезке СН, пользуясь перпендикулярностью плоскостей?

Подсказка 3

Из равенства треугольников можно вывести, что ВН = АН, то есть Н совпадает с К, значит △ADB и △AСB не только прямоугольные, но и...?

Подсказка 4

Отметьте L и M — середины рёбер BD и CD соответственно. Что можно сказать о связи LM и BC? А о LK и AD? Осталось внимательно рассмотреть △MLK и записать ответ!

Показать ответ и решение

Сразу отметим, что, поскольку центр сферы, описанной около тетраэдра, лежит на $AB$ , углы $ACB$ и $ADB$ - прямые. Далее, опустим перпендикуляры $CK$ и $CL$ на $AB$ и $BD$ соответственно. Тогда $DL = LB$ , ибо $DC = CB$ , следовательно, $KL −$ серединный перпендикуляр к $BD$ в плоскости $ABD$ и, поскольку $∘ ∠ADB = 90$ , точка $K$ является серединой $AB$ . Значит, $AC =BC$ . Аналогично, $AD = BD.$

Итак, $AC = BC = AD =BD =CD, AB ⊥CK, AB ⊥DK, AK = BK = CK =DK$ . Пусть $E −$ точка, симметричная точке $C$ относительно $K$ . Тогда $AK ⊥ EK ⊥ DK$ и $AK = EK =DK$ . Следовательно, треугольник $ADE −$ равносторонний. При этом $AE ∥CB$ . Стало быть, искомый угол равен углу $EAD$ и равен $∘ 60.$

Ответ:

$60∘$

Ошибка.
Попробуйте повторить позже

Задача 16#63816

Дан параллелепипед $ABCDA ′B′C′D′$ с основаниями $ABCD, A ′B′C′D′$ и боковыми рёбрами $AA ′,BB′,CC′,DD ′$ . Все рёбра параллелепипеда равны. Плоские углы при вершине $B$ также равны. Известно, что центр сферы, описанной около тетраэдра $′ ′ AB CD$ , лежит в плоскости $′ AB C$ . Радиус этой сферы равен 2. Найдите длину ребра параллелепипеда.

Источники: ДВИ - 2021, вариант 216, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

В вершине В сходятся 3 равных угла, что можно сказать об отрезках-диагоналях граней, лежащих напротив этой вершины? (Строго обосновать этот факт можно через треугольники, равные по 2-м сторонам и углу между ними!)

Подсказка 2

В какой ещё из вершин параллелепипеда сходятся 3 равных угла? Какой вывод можно сделать об отрезках-диагоналях граней, исходящих из этой же вершины?

Подсказка 3

Каким свойством в таком случае обладает тетраэдр D'AB'C: у него равны боковые рёбра и в основании лежит правильный треугольник? Таким образом мы можем вычислить все его стороны!

Подсказка 4

Восстановите длину стороны ромбов-граней по найденным диагоналям и можно записывать ответ!

Показать ответ и решение

Грани параллелепипеда являются ромбами. Поскольку плоские углы при вершине $B$ равны, равны также и плоские углы при вершине $′ D$ . Стало быть, $′ ′ ′ ′ AD = B D = CD$ как равные диагонали ромбов и, по той же причине, $′ ′ AB = BC = AC$ . Таким образом, центр сферы, описанной около тетраэдра $′ ′ AB CD$ , является центром окружности, описанной около правильного треугольника $′ AB C$ , а также является основанием высоты тетраэдра, опущенной из вершины $′ D$ . Отсюда получаем $′ √ - ′ √ - AB =2 3,AD =2 2$ . Итак, диагонали ромба равны $√ - 2 3$ и $√ - 2 2$ , значит, его сторона равна $√ - 5.$

Ответ:

$√5$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#63818

Вписанная в треугольную пирамиду $ABCD$ сфера касается граней $BCD, ACD,ABD$ и $ABC$ в точках $A ,B ,C 1 1 1$ и $D 1$ соответственно. Известно, что $D1$ является точкой пересечения высот треугольника $ABC$ , что плоскости $ABC$ и $A1B1C1$ параллельны и что радиус окружности, описанной около треугольника $ABC$ в четыре раза больше радиуса окружности, описанной около треугольника $A1B1C1$ . Найдите отношение, в котором сфера делит отрезок $DD1$ , считая от вершины $D.$

Источники: ДВИ - 2021, вариант 213, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

В задаче фигурирует ортоцентр, это явно неспроста. Пусть А2, B2, C2 - вершины ортотреугольника и О - центр сферы. Что можно заметить?

Подсказка 2

Представляют интерес четырехугольники OA1A2D1, OB1B2D1, OC1C2D1. На какие фигуры их можно разбить?

Подсказка 3

Они разбиваются на равные прямоугольные треугольники! Можем поотмечать равные углы и затем отметить равные отрезки.

Подсказка 4

В итоге имеем, что D1 - точка пересечения биссектрис АВС. Что тогда можем сказать?

Подсказка 5

ABC - правильный треугольник! (так как его ортоцентр совпал с инцентром) Тогда мы можем сказать какая прямая является высотой пирамиды.

Подсказка 6

Остается провести радиусы окружностей из условия и в вспомогательной плоскости поработать с нашей конструкцией.

Показать ответ и решение

Пусть $O$ — центр сферы и пусть $A ,B ,C 2 2 2$ — основания высот треугольника $ABC$ , опущенных из вершин $A,B,C$ соответственно.

$PIC$

Рассмотрим четырёхугольники $OA1A2D1$ , $OB1B2D1,OC1C2D1$ . Каждый из них состоит из двух равных прямоугольных треугольников. При этом катеты $OD1,OA1,OB1, OC1$ равны.

Из равенства расстояний от $A1,B1,C1$ до плоскости $ABC$ следует, что равны углы $D1OA1,D1OB1,D1OC1$ , а стало быть, равны и углы $D1A2A1$ , $D1B2B1,D1C2C1$ . Значит, равны отрезки $D1A2,D1B2,D1C2$ , то есть $D1$ является точкой пересечения биссектрис треугольника $ABC$ . При этом $D1$ это ортоцентр $ABC$ . Стало быть, треугольник $ABC$ правильный. Поскольку углы $D1A2A1,D1B2B1,D1C2C1$ равны, $DD1$ — высота пирамиды. Опустим из $A1$ перпендикуляр $A1D2$ на $DD1$ . Тогда радиус окружности, описанной около треугольника $A1B1C1$ равен $A1D2$ . Радиус же окружности, описанной около треугольника $ABC$ равен $AD1$ . Получаем, что $A2D1 = 1AD1 = 1 ⋅4A1D2 = 2A1D2 2 2$ . Отсюда видим, что $∠D1A2A1 = 60∘$ . Стало быть, $DD1 = √3⋅A2D1 = √3⋅√3⋅OD1 = 3OD1$ . Получаем, что искомое отношение равно $(DD1 − 2OD1 ):2OD1 = 1:2.$

Ответ:

$1 :2$

Ошибка.
Попробуйте повторить позже

Задача 18#63819

Сфера касается всех рёбер тетраэдра $ABCD$ . Известно, что произведения длин скрещивающихся рёбер равны. Известно также, что $AB = 3,BC = 1$ . Найдите $AC.$

Источники: ДВИ - 2021, вариант 215, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Подумаем, как можно применить условие о том, что сфера касается всех рёбер тетраэдра? Более всего с длинами рёбер тут связывается свойство касательных: отрезки касательных к сфере, проведенных из одной точки, равны! Обозначьте одной буквой все равные отрезки проведённые из каждой из вершин и при помощи этих букв запишите равенство произведений длин скрещивающихся рёбер. ---

Подсказка 2

Поработайте теперь с нашим двойным равенством: рассмотрите две пары уравнений и попробуйте их преобразовать. Какие интересности связанные с отрезками касательных из разных вершин можно заметить?

Подсказка 3

Если сделать всё аккуратно, то получится несколько вариантов: равны либо отрезки касательных проведённые из вершин А и С, либо проведённые из вершин В и D. Рассмотрите оба случая, не выходит ли в одном из них противоречий с условием задачи? (Не зря же нам даны AB и BC). Аналогично рассмотрите вторую пару вершин, отрезки касательных из которых равны. Останется лишь внимательная арифметика и АС откроется нам!

Показать ответ и решение

Расстояния от вершины $A$ до точек касания сферы с рёбрами $AB,AC,AD$ равны. Обозначим это расстояние $a$ . Соответствующие расстояния от вершин $B,C,D$ обозначим $b,c$ , $d$ соответственно. По условию $(a+ b)(c+ d)=(a+ c)(b+d)= (a+ d)(b+c)$ , что равносильно после раскрытия скобок системе

(a− c)(b− d)= 0 и (a − b)(c− d)= 0.

Если $a= c$ , то $AB =BC$ , а это не так. Значит, $b= d$ . Тогда либо $a= b$ , либо $c =b$ . Если $a =b$ , то $AC = BC = 1$ , что противоречит неравенству треугольника. Значит, $c=b$ и, стало быть, $AC =AB = 3.$

Замечание.

Тетраэдр, у которого произведения длин скрещивающихся рёбер равны, называется каркасным, можете поизучать его свойства. В задаче по сути просили доказать, что у такого тетраэдра суммы длин скрещивающихся рёбер равны.

Ответ:

$3$

Ошибка.
Попробуйте повторить позже

Задача 19#63813

Дана треугольная призма $ABCA ′B ′C′$ с основанием $ABC$ и боковыми рёбрами $AA′,BB′,CC ′$ . На диагоналях $AB′,BC′,CA ′$ отмечены точки $D,E,F$ соответственно. Найдите отношение, в котором плоскость $DEF$ делит отрезок $′ AA$ , если $′ ′ AD :DB =1 :1,BE :EC = 1:2$ , $′ CF :FA =1 :3.$

Источники: ДВИ - 2020, вариант 201, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Надо как-то разобраться с плоскостью DEF и отрезком AA'. Для этого можно, например, отыскать какую-нибудь плоскость, в которой будут две точки нашей плоскости DEF и отрезок AA'. Потенциально это могут быть плоскости ABB'A' и ACC'A', в которых есть по одной точке из плоскости DEF. Как бы нам найти еще какую-нибудь точку?

Подсказка 2

Грани нашей призмы являются параллелограммами, поэтому D- не только середина AB', но и A'B. Стало быть точка D лежит еще и в плоскости BA'C', в которой лежит еще и точка E. Тогда если провести прямую ED, она пересечет луч C'A' в какой-то точке P. Ураааа! Вторая точка найдена. Осталось только понять в каком отношении FP делит A'A. Для начала поймите, как относятся PA' и A'C'...

Подсказка 3

С помощью теоремы Менелая вы легко убедились, что PA'=A'C'. У нас осталась совсем простая задачка: В параллелограмме ACA'P точка F делит A'C в отношении 3:1, а нужно найти как PF делит AA'.

Подсказка 4

Если вы еще не решили ее, то советую продлить отрезок PF до пересечения с AC в точке Q и посмотреть, как относятся PA' и AQ.

Показать ответ и решение

Точки $D$ и $F$ лежат в плоскости $BCA ′$ . Обозначим через $G$ точку пересечения прямой $DF$ с прямой $BC$ .

$PIC$

Из того, что $AD :DB ′ =1 :1,CF :FA ′= 1:3$ , следует, что $GC = 12BC$ . Обозначим через $H$ точку пересечения прямой $GE$ с прямой $CC ′$ . Из того, что $GC = 12BC$ и $BE :EC ′ = 1:2$ , следует, что $CH = 17CC ′$ . Обозначая через $K$ точку пересечения прямой $HF$ с прямой $AA′$ , получаем $KA ′ = 37AA′$ . Стало быть, $A ′K :KA = 3:4.$

Ответ:

$3 :4$

Ошибка.
Попробуйте повторить позже

Задача 20#63817

В основании четырёхугольной пирамиды $ABCDS$ лежит параллелограмм $ABCD$ . На ребре $SB$ отмечена точка $E$ , так что $SE :EB = 2:1$ . На ребре $SD$ отмечена точка $F$ , так что $SF :FD = 1:2$ . Найдите отношение, в котором плоскость $AEF$ делит объём пирамиды.

Источники: ДВИ - 2020, вариант 205, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Попробуем как-то воспользоваться данными в условии отношениями…быть может, сделаем такое дополнительное построение, чтобы указанные в условии отрезки были в подобных треугольниках?

Подсказка 2

Проведите через точки B, C, D прямые, параллельные AS, и отметьте их точки пересечения B’, C’, D’ соответственно с плоскостью AEF. Что можно сказать о B’B, C’C, D’D?

Подсказка 3

B’B = 1/2 AC, D’D = 2AS, C’C = 5/2AS. Давайте теперь подумаем, как нам было бы удобнее считать объём? Быть может, разбить нашу пирамиду на несколько частей поменьше?

Подсказка 4

Выразите объем пирамиды через объемы ABDS и BCDS

Показать ответ и решение

Проведём через точки $B,C,D$ соответственно прямые $l ,l ,l B C D$ , параллельные $AS$ . Обозначим через $B′,C′,D′$ соответственно точки пересечения плоскости $AEF$ с прямыми $lB,lC$ , $lD$ .