Тема Счёт отрезков в стерео

Расстояние между скрещивающимися

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела счёт отрезков в стерео

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#63896

Дан куб $ABCDA ′B′C′D ′$ с основанием $ABCD$ и боковыми рёбрами $AA′$ , $BB′$ , $CC′$ , $DD ′$ . Найдите расстояние между прямой, проходящей через середины рёбер $AB$ и $′ AA$ , и прямой, проходящей через середины рёбер $′ BB$ и $′′ B C$ , если ребро куба равно $1.$

Подсказки к задаче

Подсказка 1

Перед нами встала задача вычислить расстояние между скрещивающимися прямыми, какие способы сделать это вы знаете? Общий перпендикуляр тут не то чтобы очевиден, а вот параллельные плоскости можно попробовать построить! Проведём через середину ВВ' прямую, параллельную прямой проходящей через середины АВ и АА'. Одно сечение прямо перед нами! Назовём эту плоскость α.

Подсказка 2

Второе сечение построить чуть сложнее, но опираясь на знание о том, что параллельные плоскости пересекают третью по параллельным прямым, мы можем сделать и это. Назовём такую плоскость β.

Подсказка 3

Рассмотрим пересечение плоскостей α и (BB'D). В каком отношении плоскость α делит диагональ куба B'D? А что можно сказать про угол между диагональю куба B'D и плоскостью α?

Подсказка 4

Аналогично можно выяснить и про плоскость β: она будет перпендикулярна диагонали куба. Тогда расстояние между α и β равно длине отрезка диагонали куба заключённого между ними. Рассматривая пересечение плоскостей β и (BB'D) можно установить, в каком отношении плоскость β делит нашу диагональ? Немного арифметики и задача решена!

Показать ответ и решение

Пусть $E,F,K,L,M$ — середины рёбер куба $AA ′,$ $AB,$ $B′C ′,$ $B ′B,$ и $B′A′$ соответственно.

$PIC$

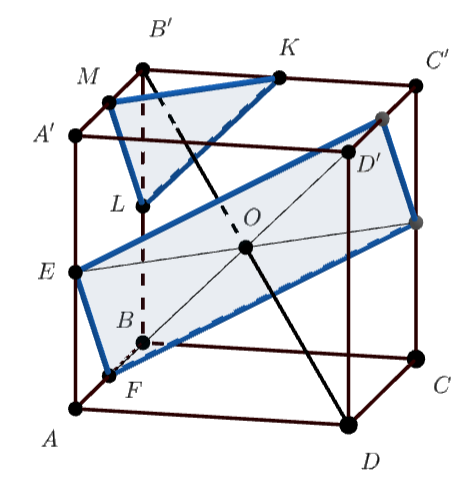
Проведем плоскость через $E,F$ и центр $O$ куба. Данная плоскость перпендикулярна диагонали $B ′D,$ так как $EO||AC,F O||AD′$ , а прямые $AC, AD′$ перпендикулярны $B ′D$ . Так как плоскость $EOF$ проходит через $O,$ она делит $B′D$ в отношении $1 :1.$

Прямая $KL$ лежит в плоскости $KLM$ , которая также перпендикулярна диагонали $B′D.$ При этом плоскость делит диагональ $B ′D$ в отношении $1:5,$ поскольку плоскость $KLM$ проходит через середины ребер $B′C ′,$ $B ′B,$ и $B′A′$ и параллельно плоскости $A′BC ′,$ которая делит $B ′D$ в отношении $1:2.$