Тема Всесиб (Всесибирская открытая олимпиада школьников)

Отбор Всесиба

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела всесиб (всесибирская открытая олимпиада школьников)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#87885

На отрезке $AB$ , как на диаметре, построен полукруг, в котором точка $M −$ середина дуги $AB$ . На дуге $BM$ выбрана произвольная точка $K$ , отличная от $B$ и $M$ , через $P$ обозначена точка пересечения прямых $AB$ и $MK$ . Пусть $T$ — точка пересечения прямой $AK$ и перпендикуляра к прямой $AB$ , проведённого через точку $P$ . Докажите, что длины отрезков $BP$ и $PT$ равны.

Подсказки к задаче

Подсказка 1

Первое, что бросается в глаза — большое количество прямых углов на картинке. Прямой ВРТ говорит о том, что для решения задачи достаточно доказать, что угол ТВР, например, равен 45 градусам. Что ещё, связанное со вписанностью и прямыми углами, можно указать на картинке?

Подсказка 2

Хочется показать, что на картинке имеется вписанный четырехугольник, используя один из признаков такого четырехугольника. Также осталось вспомнить, что точка М — середина дуги АВ окружности, это тоже важно для некоторых углов!

Показать доказательство

Для начала заметим, что $∠AKB = 90∘,$ так как $AB$ — диаметр полуокружности. По условию прямая $TP$ — перпендикуляр к $AB$ , то есть $∘ ∠BPT = 90.$ Тогда в четырехугольнике $BKT P$ внутренний угол $BP T$ равен внешнему углу $AKB$ при противоположной вершине. Значит, четырёхугольник $BKT P$ вписанный.

$PIC$

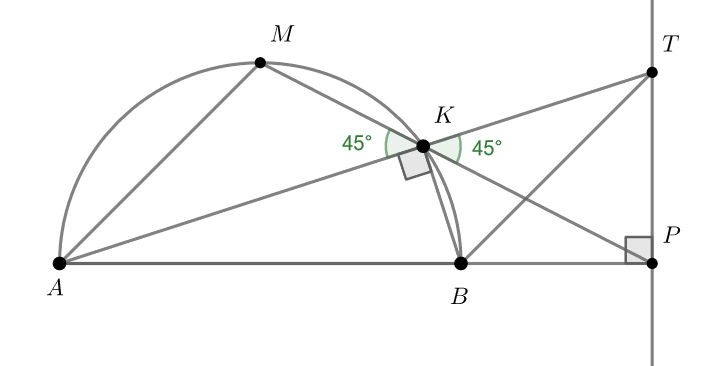
Так как $M$ — середина полуокружности, $⌣ AM = 90∘,$ а опирающийся на эту дугу вписанный угол $∠AKM = ⌣A2M-= 45∘.$

$∠TKP = ∠AKM,$ как вертикальные углы, а $∠TKP =∠T BP,$ потому что $BKT P$ — вписанный четырехугольник.

Тогда $∠T BP =∠T KP = ∠AKM =45∘,$ то есть прямоугольный треугольник $BPT$ имеет угол в $45∘.$ Значит, $△BP T$ — равнобедренный и $BP = PT.$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#95862

По кругу сидят рыцари и лжецы — всего $12$ человек. Каждый из них сказал фразу: “Все сидящие за столом, кроме, может быть, меня и моих соседей, лжецы”. Сколько за столом рыцарей, если рыцари всегда говорят правду, а лжецы всегда лгут?

Подсказки к задаче

Подсказка 1

Давайте поразмышляем, если за столом есть хотя бы один рыцарь, то сколько за этим столом гарантированно будет лжецов?

Подсказка 2

Наш рыцарь про каждого, кто не является его соседом, скажет, что тот лжец, значит за столом будет минимум 9 лжецов. Подумайте, могут ли за столом оказаться три рыцаря?

Показать ответ и решение

Если за столом больше двух рыцарей, то какие-то два из них не соседи и ни один из них не может сказать, что все за столом, кроме, может быть, него и его соседей, лжецы, ибо это будет ложью. Если за столом один рыцарь, то для любого лжеца, соседнего с ним, эта же фраза будет правдой, которую ему говорить не положено. Тоже самое будет верно для любого лжеца, если за столом вообще нет рыцарей.

Ответ:

$2$

Ошибка.
Попробуйте повторить позже

Задача 3#72734

Найти все пары натуральных чисел $x$ и $y$ таких, что их наименьшее общее кратное равно $1+ 2x+3y.$

В качестве ответа введите все возможные значения $x$ через пробел в порядке возрастания.

Источники: Всесиб-2019, отбор

Подсказки к задаче

Подсказка 1

Из условия следует, что 1+3y делится на x, а 1+2x делится на y. Кажется, что это может дать нам неплохие оценки на x и y...

Подсказка 2

Пускай для начала 1<x≤y. Из делимости 1+3y на x следует, что 1+2x=ky. Если k>2, то x>y. Тогда k=1 или k=2. Какой из случаев не реализуется?

Подсказка 3

При k=2, 1+2x должно делится на 2, что неверно. Тогда 1+2x=y ⇒ 4+6x делится на x. Следовательно, x надо искать среди делителей 4. Пускай теперь x>y>1. Что мы можем сказать про k, где 1+3y=kx?

Подсказка 4

Верно, k<4! При этом k не может равняться 3. Если k=2, то 1+3y=2x ⇒ y=2t+1, x=3t+2. При этом 1+2x=6t+5 должно делится на 2t+1. Посмотрите на НОД(6t+5, 2t+1) и разберитесь со случаем k=1!

Показать ответ и решение

Пусть сначала $x≤ y$ Заметим, что $y$ не может делиться на $x,$ иначе наименьшее общее кратное $x$ и $y$ равно $y,$ а это меньше $1+ 2x+ 3y.$ В частности, $x> 1.$

Далее, наименьшее общее кратное $x$ и $y$ делится на $x$ и $y,$ поэтому $1+ 2x +3y$ делится на $x$ и $y,$ а значит $1+2x$ делится на $y$ и $1+3y$ делится на $x.$ Из делимости $1+ 2x$ на $y$ следует $1 +2x= ky ≥ y,$ что вместе с предположением $x≤ y$ влечёт $k =1,y = 2x+ 1.$ Тогда из делимости $1+ 3y =6x+ 4$ на $x$ и $x> 1$ следуют делимость 4 на $x$ и возможности $x= 2,4.$ Проверка показывает, что решением в этом случае является $x =4,y = 9.$

Теперь рассмотрим случай $x≥ y > 1,$ из делимости $1 +3y ≤ 1+ 3(x− 1)= 3x − 2$ на $x$ следует $1+3y =x$ или $1+ 3y = 2x.$ Если $1+ 3y = x,$ то $1+ 2x= 6y +3$ делится на $y,$ тогда $3$ делится на $y$ и $x= 10,y =3$ является решением задачи.

Если $1+3y =2x,$ то $y$ нечётно, $y =2k +1,k> 0,x =3k+ 2.$ Тогда $1+ 2x =6k +5$ должно делиться на $y = 2k+ 1,$ значит $6k+ 5− 3(2k+ 1)=2$ делится на $y =2k +1≥ 3,$ что невозможно.

Ответ: 4 10

Ошибка.
Попробуйте повторить позже

Задача 4#68485

Точка $I$ — центр вписанной в треугольник $ABC$ окружности. Внутри треугольника выбрана такая точка $P$ , что $∠P BA+ ∠PCA = ∠PBC + ∠PCB$ . Докажите, что $AP ≥ AI$ , причём равенство выполняется тогда и только тогда, когда точка $P$ совпадает с точкой $I$ .

Источники: IMO - 2006, Problem 1 и Отборочный Всесибирской олимпиады - 2018

Подсказки к задаче

Подсказка 1

Сразу бросается в глаза неприятное равенство на сумму углов. Заметим, что было бы хорошо, если бы угол PBC складывался с PBA и PCA c PCB. Как мы можем этого добиться? Конечно, сложить левую часть равенства с правой, а затем повыражать неизвестные нам углы через углы треугольника ABC!

Подсказка 2

Мы получаем, что углы BPC и PIC = 90 + (угол A) / 2. Вспомним лемму о трезубце! Точки B,P,C,I будут лежать на одной окружности. Иначе, P будет лежать на описанной окружности треугольника BCI. Но где же находится центр этой окружности?

Подсказка 3

Конечно, вновь используя лемму о трезубце, мы понимаем что центр M окружности BCI лежит на середине дуги BC. Более того, M лежит на описанной окружности треугольника ABC. Это в точности значит, что M лежит на биссектрисе угла BAC. Помним, что нам необходимо доказать неравенство на отрезки. Обычно в таких ситуациях необходимо применить неравенство треугольника! Для какого треугольника неравенство будет наиболее подходящим?

Подсказка 4

Конечно для треугольника APM, ведь AM = AI + IM и IM = IP(как радиусы)

Показать доказательство

$PIC$

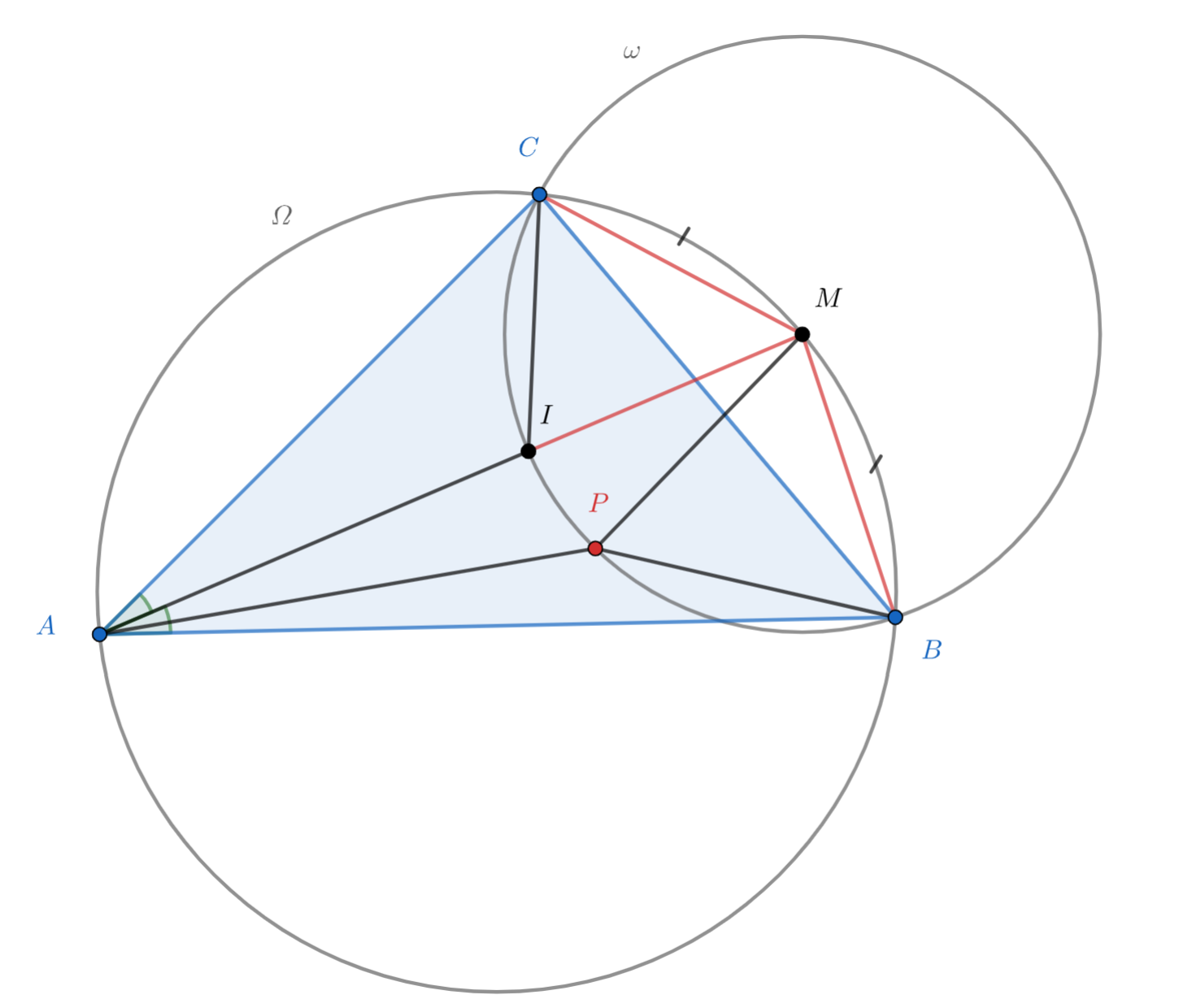
Пусть $∠A = α, ∠B = β, ∠C =γ.$

Поскольку $∠PBA + ∠PCA + ∠PBC + ∠PCB = β+ γ$ условие задачи эквивалентно $∠PBC + ∠PCB = (β +γ)∕2$ , т.е. $∠BP C =π∕2+ α∕2$ .

С другой стороны, $∠PIC =π − (β+ α)∕2= π∕2+ α∕2$ . Следовательно, $∠BPC = ∠PIC$ , и т.к. точки $P$ и $I$ лежат по одну сторону от $BC$ , точки $B, C, I$ и $P$ лежат на одной окружности. Иными словами, $P$ лежит на $ω$ — описанной окружности $△BCI.$

Пусть $Ω$ — описанная окружность $△ABC$

Легко проверить, что центр окружности $ω$ совпадает с точкой $M$ — серединой дуги $BC$ и лежит на $Ω$ , а значит — и на биссектрисе угла $CAB.$

Из неравенства треугольника (для $△AP M$ ) следует

|AP|+ |PM |≥|AM |=|AI|+|IM|= |AI|+ |P M|

Поэтому $|AP|≥ |AI|$ . Равенство достигается тогда и только тогда, когда $P$ принадлежит $AI$ , что означает $P = I.$

Ошибка.
Попробуйте повторить позже

Задача 5#74603

(a) Квадрат размера $1×1$ разбит на 25 не обязательно одинаковых прямоугольников, каждый из которых имеет одинаковый периметр $p$ . Найти минимальное и максимальное возможное значение $p$ .

(b) Можно ли разбить единичный квадрат на 30 не обязательно одинаковых прямоугольников периметра 2?

Подсказки к задаче

Пункт а), подсказка 1

Если мы разбиваем прямоугольник на 25 маленьких, тогда что можно сказать про площадь самого большого из них?

Пункт а), подсказка 2

Верно, она должна быть не меньше 1/25. В таком случае, можно оценить его периметр по неравенству о средних!

Пункт а), подсказка 3

Да, по неравенству о средних его периметр будет не меньше 0.8, нужно только показать, что это значение достигается. Для оценки максимума попробуйте написать оценки на прямоугольник площадь которого не больше 1/25.

Пункт а), подсказка 4

Да, площадь какого-то прямоугольника(причем он обязательно существует) не больше 1/25. Можно обозначить его стороны за a и b, причем каждое из них не больше единицы! В таком случае, будет верно, что a*(p/2-1) ≤ 1/25. Осталось исследовать эту функцию(где она принимает минимальные значения) и привести пример!

Пункт б), подсказка 1

Попробуем перейти от исходного квадрата к другому квадрату поменьше, который мы можем замостить одинаковыми прямоугольниками! Что для этого можно сделать?

Пункт б), подсказка 2

Да, можно вырезать «рамку» из исходного прямоугольника с помощью четырех прямоугольников размером x*(1-x). Тогда, в центре останется квадрат размером (1-2x)*(1-2x). Что можно попробовать сделать с этим квадратом?

Пункт б), подсказка 3

Да, этот квадрат можно попробовать разрезать на 26 равных, площадь каждого из которых будет: (1-2x)*(1-2x)/26. А дальше вспоминаем, что периметр такого прямоугольника должен быть равен 2!

Показать ответ и решение

(a) Один из прямоугольников разбиения должен иметь площадь не меньше, чем $1- 25$ , обозначим его стороны за $x$ и $y$ . По неравенству о среднем арифметическом и средним геометрическом имеем

x+y √-- ∘-1- 1 -2--≥ xy ≥ 25-= 5 =⇒ p= 2(x+ y)≥ 0,8

Значение $p= 0,8$ достигается для разбиения квадрата на $25$ одинаковых квадратиков со стороной $0,2.$

По принципу Дирихле в любом разбиении единичного квадрата на $25$ прямоугольников найдётся прямоугольник (обозначим его стороны за $x≤ 1$ и $y ≤ 1$ ) площади $S$ не больше $125.$ При этом $x = p2 − y ≥ p2 − 1.$ Следовательно, $( ) S = x p2 − x ≤ 125$ для $[ ] x ∈ p2 − 1;1.$ Функция $S(x)$ является квадратичной с отрицательным старшим коэффициентом, поэтому её минимум на отрезке принимается в одном из концов этого отрезка. Соответствующие значения на концах равны $p2 − 1.$ Следовательно,

p − 1≤-1 ⇐ ⇒ p ≤2,08 2 25

Разбиение квадрата на $25$ равных прямоугольников со сторонами $1$ и $-1 25$ даёт пример $p =2,08$

(b) Приведем алгоритм разбиения квадрата на 30 прямоугольников периметра 2. Понятно, что нужно каким-то образом уменьшить разрезаемый квадрат, потому что его стороны слишком большие.

Попробуем отрезать от исходного квадрата $1 ×1$ "рамку"из четырех прямоугольников. Для этого выберем некоторое число $x< 1. 2$ Теперь отрежем от исходного квадрата четыре прямоугольника размером $x ×(1− x)$ так, чтобы в центре остался квадрат размером $(1− 2x)× (1− 2x).$

$x1− x$

Разобьем теперь центральный квадрат на 26 равных прямоугольников размером

(1− 2x)× 1−-2x 26

Их периметр равен 2, поэтому получаем уравнение

2(1− 2x + 1-− 2x)= 2 26

Таким образом, $x= -1. 54$ В итоге получаем следующее разбиение.

$x1− x$

Ответ:

(a) $0,8;2,08$

(b) да

Ошибка.
Попробуйте повторить позже

Задача 6#96340

Можно ли число $2016$ представить в виде суммы нескольких попарно различных натуральных чисел таких, что среди всех возможных попарных сумм этих чисел ровно $7$ различных?

Источники: Всесиб - 2017, отбор, 10.5(см. sesc.nsu.ru)

Подсказки к задаче

Подсказка 1

Попробуем пойти от противного. Тогда 2016 можно представить в виде суммы n попарно различных чисел. Всего пар чисел можно составить n(n-1)/2. Какая нижняя оценка получается на n?

Подсказка 2

Верно! Должно получиться не менее 7 пар, и поэтому n ≥ 5. С другой стороны, наши числа можно упорядочить по возрастанию. Складывая наименьшее число последовательно со всеми остальными, получим n-1 различное число. А можно ли аналогично получить еще суммы, которые отличаются от уже построенных?

Подсказка 3

Можно! Последнее из уже получившихся чисел представляет собой сумму первого и последнего числа. Тогда можно складывать последнее число последовательно со вторым, третьим и так далее. Мы получим n-2 попарно различных числа, отличающихся от первых n-1. Как теперь можно сверху оценить n?

Подсказка 4

Верно! Всего получится 2n-3 различных числа, а их должно быть не больше 7, поэтому n ≥ 5. Выходит, что n = 5! Теперь легко выписать все возможные суммы наших чисел. Всего получится 10 сумм, а среди них только 7 различных. Причем ранее мы уже указали 7 попарно различных сумм! Попробуем теперь рассмотреть три оставшихся. С какими другими суммами они должны совпадать?

Подсказка 5

Ясно, что мы не рассматривали суммы между вторым и третьим, вторым и четвертым, третьим и четвертым числами. Кроме того, понятно, что они попарно различны. Благодаря тому, что остальные 7 сумм нам удалось упорядочить, можно найти среди них суммы, которые должны совпадать с нашими тремя. Как это сделать?

Подсказка 6

Верно! Они должны совпадать с суммами первого и четвертого, первого и пятого, второго и пятого чисел! Тогда можно вычесть равенства и заметить, что все наши числа образуют арифметическую прогрессию. Могло ли так получиться?

Показать ответ и решение

Предположим, что $2016$ можно представить в виде суммы попарно различных натуральных чисел $a < a < ...< a 1 2 n$ таких, что среди всех возможных попарных сумм этих чисел ровно $7$ различных. Общее количество пар из $n$ чисел равно $n(n−1) 2$ и должно быть не меньше $7,$ поэтому $n≥ 5.$ С другой стороны, ввиду очевидных неравенств:

a1 +a2 < a1+ a3 < ...< a1 +an < a2+ an < ...< an−1+an

имеем $n− 1+n − 2 =2n− 3≤ 7$ и $n ≤5.$ Следовательно, $n =5$ и каждая невыписанная попарная сумма чисел $a <a < ...< a 1 2 n$ равна одной из семи сумм, рассмотренных в длинном неравенстве. Всего нерассмотренных сумм три:

a2+ a3 < a2+a4 <a3+ a4

и все они больше $a1+a3$ и меньше $a3+ a5.$ По условию, они должны совпадать с суммами

a + a < a +a <a + a 1 4 1 5 2 5

в указанном порядке. Отсюда: $a2− a1 =a4− a3 = a5− a4 =a3− a2,$ следовательно, числа $a1 < a2 < ...< a5$ образуют арифметическую прогрессию. Тогда их сумма равна $5⋅ a1+2a5= 2016$ , откуда следует, что число $4032$ должно делиться на $5$ — противоречие.

Ответ:

Нельзя

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#98814

Найдите все решения уравнения:

2 2 2 cos x+ cos 2x+ cos 3x= 1.

Подсказки к задаче

Подсказка 1

Слева у нас есть и двойной угол, и тройной угол — давайте попробуем их раскрыть по формулам и привести подобные!

Подсказка 2

Если справа останется 0, то слева будет уравнение с шестой, четвёртой и второй степенью косинуса! Как будем такое решать?)

Подсказка 3

Вынесем за скобки общий множитель! Тогда останется биквадратное уравнение, которое несложно решить ;)

Показать ответ и решение

По формулам $cos2x= 2cos2x− 1,cos3x= 4cos3x− 3cosx$ после преобразований получаем

6 4 2 8cos x− 10cos x+ 3cos x= 0,

откуда

-1- √3- cosx= 0 или cosx = ±√2 или cosx= ± 2 .

Следовательно,

x= π2 +πk или x= π4 + π2kили x= ±π6 +πk (k∈ℤ)

Ответ:

$π + πk;π + πk;± π+ πk (k∈ ℤ) 2 4 2 6$

Ошибка.
Попробуйте повторить позже

Задача 8#89609

На острове живёт нечётное число людей, причём каждый из них либо рыцарь, который всегда говорит правду, либо лжец, который всегда лжёт. Как-то раз все рыцари заявили: “Я дружу только с 1 лжецом”, а все лжецы: “Я не дружу с рыцарями”. Кого на острове больше, рыцарей или лжецов?

Показать ответ и решение

Каждый лжец дружит хотя бы с одним рыцарем. Но так как каждый рыцарь дружит ровно с одним лжецом, у двух лжецов не может быть общего друга-рыцаря. Тогда каждому лжецу можно поставить в соответствие его друга рыцаря, откуда получается, что рыцарей, по крайней мере, столько же, сколько и лжецов. Так как всего жителей на острове нечётное число, то равенство невозможно. Значит, рыцарей больше.

Ответ: рыцарей

Ошибка.
Попробуйте повторить позже

Задача 9#94878

В каждой клетке таблицы $10$ на $10$ записан минус. За одну операцию разрешается одновременно менять на противоположные знаки во всех клетках некоторого столбца и некоторой строки (плюс на минус и наоборот). За какое минимальное количество операций можно добиться того, что все знаки в таблице станут плюсами?

Показать ответ и решение

Всего в строке и столбце, проходящих через данную клетку 19 клеток, поэтому если мы проделаем операции со всеми парами строк и столбцов таблицы (всего операций), то каждый знак в таблице поменяется 19 раз, став из минуса плюсом.

100 операций достаточно.

_________________________________________________________________________________________________________________________________________________________________________________

Операцию замены знаков во всех клетках некоторого столбца и некоторой строки будем называть операцией относительно клетки-пересечения этих строки и столбца. Клетки, относительно которых мы делали операции, назовём красными, остальные синими. Строки и столбцы, содержащие чётное число красных клеток назовём чётными, а содержащие нечётное число красных клеток — нечётными.

_________________________________________________________________________________________________________________________________________________________________________________

Допустим, можно поменять все знаки в таблице меньше чем за 100 операций, тогда рассмотрим некоторую синюю клетку $A$ в строке $X$ и столбце $Y$ . Чтобы знак в $A$ поменялся, нужно, чтобы, чтобы $X$ и $Y$ вместе содержали нечётное количество красных клеток, можно считать строку $X$ чётной, а столбец $Y$ — нечётным.

Заметим, что на пересечении строки и столбца одинаковой чётности должна стоять красная клетка, а на пересечении строки и столбца разной чётности — синяя, иначе знак в этой клетке после всех операций не изменится. Следовательно, количество красных клеток в каждой чётной строке равно числу чётных столбцов, а количество синих — числу нечётных столбцов таблицы. Есть хотя бы одна чётная строка $X$ , значит, всего в таблице чётное число нечётных столбцов. Но количество красных клеток в каждой нечётной строке (нечётное!) равно числу нечётных столбцов, то есть чётному числу — противоречие с тем, что есть хотя бы один нечётный столбец. Следовательно, нельзя обойтись меньше, чем 100 операциями.

Ответ: 100

Ошибка.
Попробуйте повторить позже

Задача 10#98019

Натуральные числа таковы, что $a+ c= 1000$ , $b+ d= 500.$ Найти максимальное значение суммы $a+ c. b d$

Показать ответ и решение

Ввиду симметрии можно считать, что $b≥ d$ . Тогда при замене пары $a,c$ на пару $a− 1,c+ 1$ , получим

( a− 1 c+1) (a c) 1 1 -b--+ -d-- − b + d = d − b ≥ 0

увеличение искомого выражения, следовательно, максимум нужно искать среди дробей $1b + 999d$ . При замене пары $b,d$ на пару $b+ 1,d − 1$ , получим

( ) ( ) --1-+ -999- − 1+ 999 = --999-- −---1-- b+ 1 d− 1 b d d(d− 1) b(b+1)

Ввиду того, что $b≥ d$ , имеем

b(b+ 1)≥d(d+1)> d(d− 1),

поэтому

--999- > --1---> --1--- d(d− 1) d(d− 1) b(b+ 1)

и предыдущая разность положительна. Следовательно, максимум выражения достигается при $a= 1,b =499,c =999,d =1$ и равен $-1- 999- 499 + 1 .$

Ответ:

$-1-+ 999 499$

Ошибка.
Попробуйте повторить позже

Задача 11#67155

В семье $4$ человека. Если Маше удвоят стипендию, общий доход всей семьи возрастет на $5%,$ если вместо этого маме удвоят зарплату — на $15%,$ если же зарплату удвоят папе — на $25%.$ На сколько процентов возрастет доход всей семьи, если дедушке удвоят пенсию?

Источники: ММО-2003, 8.1 и отборочный этап Всесибирской олимпиады - 2016, 8 класс

Подсказки к задаче

Подсказка 1

Подумаем, откуда же взялись 5%, на которые увеличился доход семьи?) Что в его составе?

Подсказка 2

После того, как к общему доходу добавили 1 зарплату Маши, общий доход увеличился на 5%) Значит, заплата Маши это...?)

Подсказка 3

5% от общего дохода! Аналогично с мамой и папой, тогда несложно посчитать пенсию дедушки)

Показать ответ и решение

При удвоении стипендии Маши общий доход всей семьи увеличивается ровно на величину этой стипендии, значит, она составляет $5%$ от общего дохода. Аналогично, зарплаты мамы и папы составляют $15%$ и $25%.$ Значит, пенсия дедушки составляет $100 − 5− 15− 25 =55$ процентов. Если её удвоят, то доход семьи возрастёт на $55%.$

Ответ:

$55%$

Предыдущий раздел

Следующий раздел