№15 из ЕГЭ 2015
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
ОДЗ:
Сделаем замену , тогда
Решим это неравенство методом интервалов:

откуда .
, что можно представить в виде
или
.
Решим первое из этих неравенств:
Это неравенство на ОДЗ равносильно:
Решим второе из этих неравенств:
Это неравенство на ОДЗ равносильно:
Объединенное решение двух неравенств: .
Пересечем ответ с ОДЗ:
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
ОДЗ:

откуда
Решим первое из этих неравенств:
Решим второе из этих неравенств:
Пересечем полученное множество с ОДЗ:
Ошибка.
Попробуйте повторить позже
Решите неравенство
Найдем ОДЗ:
По свойству логарифма имеем:
Сделаем замену
Тогда неравенство запишется в виде
Решим это неравенство методом интервалов:

Отсюда получим
Сделаем обратную замену:
Решим первое из этих неравенств:
Решим второе из этих неравенств:
Объединеним решения двух неравенств выше:
Пересечем объединенное решение с ОДЗ:
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек, | 1 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки
в строгости неравенства: «» вместо «
» или наоборот. Если в
ответ включено значение переменной, при котором одна из
частей неравенства не имеет смысла, то выставляется оценка «0
баллов».
Ошибка.
Попробуйте повторить позже
Решите неравенство
ОДЗ логарифмов:
Сделаем замену , тогда
Решим это неравенство методом интервалов:
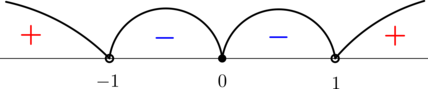
откуда .
, что можно представить в виде
Решим первое неравенство:
Это неравенство на ОДЗ равносильно:
Решим второе уравнение:
Это уравнение на ОДЗ равносильно:
Решим третье неравенство:
Это неравенство на ОДЗ равносильно:
Объединенное решение двух неравенств и уравнения: .
Пересечем ответ с ОДЗ:

