Тема Задачи №16 из ЕГЭ прошлых лет

№16 из ЕГЭ 2015

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#767Максимум баллов за задание: 2

15 января планируется взять кредит в банке на 11 месяцев. Условия его возврата таковы:
$∙$ 1-ого числа каждого месяца долг возрастает на $y%$ по сравнению с долгом на конец предыдущего месяца;
$∙$ со 2-ого по 14-ое числа каждого месяца необходимо выплатить часть долга в виде платежа банку;
$∙$ 15-ого числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-ое число предыдущего месяца. Известно, что общая сумма выплат по кредиту превысила сумму кредита на $30%$ процентов. Найдите $y$ .

Источники: ЕГЭ 2015, основная волна

Показать ответ и решение

Фраза “долг должен быть на одну и ту же сумму меньше” означает, что кредит выплачивается дифференцированными платежами. Следовательно, т.к. кредит взят на 11 месяцев, то эта “одна и та же сумма”, на которую уменьшается долг каждый месяц, равна $1- 11$ части от суммы кредита. Обозначим сумму кредита за $A$ и составим таблицу.
Так как каждый месяц долг увеличивается на $y%$ , то в первый месяц долг увеличится на $0,01y ⋅ A$ рублей, то есть составит $A + 0,01yA$ рублей.
После выплаты долг должен уменьшиться на $-1A 11$ рублей, то есть должен составить $10A 11$ рублей. Значит, выплата в первый месяц будет равна $A + 0,01yA − 10A = 0,01yA + -1A 11 11$

|----------------|---------------------------|----------------------|-------------------| |Н ом ер месяца |Дол г п осле начи сления % |Д олг после вы пла ты | Вы пла&#x |1---------------|------A-+--0,01y-⋅ A-------|---------11A----------|-0,01y-⋅-A-+-11A---| |2---------------|----1101A-+--0,01y-⋅ 1101A-----|---------911A----------|0,01y-⋅-1101A-+-111A--| |3 | -9A + 0,01y ⋅ 9-A | 8-A |0,01y ⋅ 9-A + -1A | |----------------|----11------------11-------|---------11-----------|--------11----11---| |...-------------|-----2------...---2--------|---------.1..----------|--------.2..----1---| |10--------------|----11A-+--0,01y-⋅11A------|---------11A----------|0,01y-⋅-11A-+-11A--| -11-------------------111A-+--0,01y-⋅ 111A----------------0------------0,01y-⋅-111A-+-111A--|

Заметим, что все выплаты состоят из двух частей, причем часть $-1 11A$ фиксирована.
По условию общая сумма выплат $R$ превысила на $30%$ сумму кредита $A$ . Это значит, что переплата по кредиту $R − A$ составила $30%$ от $A$ . Найдем общую сумму выплат:

$( -1 ) ( 10 1- ) ( -9 1- ) R = 0, 01y ⋅ A + 11A + 0,01y ⋅11A + 11A + 0,01y ⋅11A + 11A + ⋅⋅⋅+$

$( ) ( ) + 0, 01y ⋅ 211A + 111A + 0,01y ⋅111A + 111A =$

$= 0,01y ⋅ A (1 + 10+ 9-+ ⋅⋅⋅ + -2+ 1-) + 11 ⋅ 1-A 11 11 11 11 11$

В скобках — сумма 11 членов арифметической прогрессии, где $1 a1 = 11, a11 = 1$ . По формуле суммы арифметической прогрессии $a1-+-a11 S11 = 2 ⋅ 11$ , значит,

$( ) R = 0,01y ⋅ A ⋅ 12 111 + 1 ⋅ 11 + A = 0,06yA + A$
Тогда $R − A = 0,06yA$ . Так как переплата составила $30%$ от $A$ , то

R − A 0,06yA ---A---⋅ 100% = 30% ⇒ ---A----= 0, 3 ⇒ y = 5

Ответ:

$5$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#768Максимум баллов за задание: 2

Компании N принадлежат две шахты в разных городах. В шахтах добываются абсолютно одинаковые минералы, но в шахте, расположенной в первом городе, используется более современное оборудование. В результате, если рабочие первой шахты трудятся суммарно $t2$ часов в день, то за день они добывают $8t$ единиц минералов, а рабочие второй шахты за те же $t2$ часов в день добывают $6t$ единиц минералов. За каждый час работы компания $N$ платит каждому своему рабочему по $100$ рублей. Компания готова выделять $1000000$ рублей в день на оплату труда рабочих. Какое наибольшее количество единиц минералов можно добыть за день на этих двух шахтах?

Источники: ЕГЭ 2015, досрочная волна

Показать ответ и решение

Компания N готова оплачивать $10000$ часов в день.
Пусть $x2$ часов в день суммарно трудятся рабочие первой шахты,
Пусть $y2$ часов в день суммарно трудятся рабочие второй шахты, тогда

2 2 x + y = 10000.

Обозначим за $S$ количество суммарно добытых за день единиц минералов, тогда

S = 8x+ 6y

Так как $y = √10000-− x2$ , то

∘ --------- S(x)= 8x+ 6 10000− x2.

ОДЗ: $x∈ [− 100;100]$ . Необходимо найти наибольшее значение функции $S(x)$ при $x∈ [0;100]$ .

′ x S (x)= 8− 6⋅√10000−-x2-= 0

Критические точки функции $S(x)$ – это внутренние точки её области определения, в которых её производная равна $0$ или не определена. $S ′(x)= 0$ при $x= 80$ .

Найдём промежутки возрастания/убывания $S (x)$ на $[0;100]$ :

$PIC$

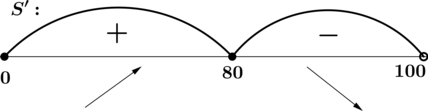
то есть $x =80$ точка локального максимума. Кроме того, $S′(x)$ не определена при $x = ±100$ . Легко убедиться, что среди этих $x$ , попадающих на отрезок $[0;100]$ , наибольшее значение $S(x)$ достигается при $x = 80$ . Более того, $S (80)> S(0)$ , следовательно, $S(80)$ – наибольшее значение функции $S (x)$ на отрезке $[0;100]$ .

S (80)= 640+ 360= 1000.

Ответ:

$1000$

Ошибка.
Попробуйте повторить позже

Задача 3#769Максимум баллов за задание: 2

Строительство нового аквапарка стоит 40 млн рублей. Затраты на обслуживание $x$ тысяч посетителей составляют $2x2+ 5x+ 3,5 3$ млн рублей в год. Если билеты продавать по цене $P$ тыс. рублей за штуку, то прибыль аквапарка в млн рублей за один год составит $Px − (23x2+ 5x+ 3,5).$ Когда аквапарк будет построен, он будет принимать посетителей в таком количестве, чтобы прибыль была наибольшей (желающих будет предостаточно). При каком наименьшем значении $P$ строительство аквапарка окупится не более чем за 4 года?

Источники: ЕГЭ 2015, резервный день

Показать ответ и решение

Так как строительство аквапарка должно окупиться не более чем за 4 года, то прибыль за 4 года должна составить не менее 40 млн руб. То есть цена $P$ должна быть такой, чтобы существовало какое-нибудь решение неравенства

( ) ( ) 4(Px − 2x2+ 5x +3,5 )≥ 40 ⇔ Px − 2x2+ 5x +3,5 ≥10 3 3 − 2x2+ (P − 5)x− 3,5 ≥ 10 ⇔ 2x2− (P − 5)x+ 13,5 ≤ 0 3 3

График левой части последнего неравенства при всяком фиксированном $P$ представляет собой параболу с ветвями, направленными вверх. Тогда у последнего неравенства есть решение тогда и только тогда, когда вершина соответствующей параболы лежит не выше оси $Ox,$ то есть $yв ≤ 0:$

2⋅(0,75(P − 5))2− (P − 5)⋅(0,75(P − 5))+ 13,5≤ 0 3

Это равносильно

3 8(P − 5)2 ≥ 13,5 ⇔ (P − 5)2 ≥36

Отсюда с учётом условия $P > 0$ получим $P ≥ 11.$

Таким образом, минимальная цена билета, при которой аквапарк имеет шанс окупиться за 4 года (при наличии достаточного количества желающих его посетить), составляет $P = 11$ тыс. рублей.

Ответ:

$11$

Ошибка.
Попробуйте повторить позже

Задача 4#2350Максимум баллов за задание: 2

Строительство нового завода стоит 76 млн. рублей. Затраты на производство $x$ тысяч единиц продукции на таком заводе равны $Z = 0,5x2 +3x +13$ млн. рублей в год. Если продукцию завода продать по цене $q$ тысяч рублей за единицу, то прибыль в млн. рублей за один год составит $qx− Z$ . Когда завод будет построен, планируется выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении $q$ строительство завода окупится не более, чем за 4 года?

Источники: ЕГЭ 2015, резервный день

Показать ответ и решение

Так как строительство завода должно окупиться не более, чем за 4 года, то прибыль за 4 года должна составить не менее 76 млн. рублей. Следовательно,

2 2 4(qx− (0,5x +3x +13))≥ 76 ⇔ qx− 0,5x − 3x − 13 ≥19

$q$ принимает такие значения, при которых прибыль (значение выражения $qx− 0,5x2 − 3x − 13$ ) будет наибольшей. Следовательно, наибольшее значение выражения $qx− 0,5x2 − 3x − 13$ должно быть $≥ 19$ .
Функция $y = qx − 0,5x2− 3x− 13= −0,5x2+ (q− 3)x− 13$ является квадратичной, ее графиком является парабола, ветви которой направлены вниз. Следовательно, наибольшее значение она принимает в своей вершине, то есть в точке $−(q−-3)- x0 = 2⋅(−0,5) = q− 3$ . Значит,

−0,5(q− 3)2+ (q − 3)(q− 3) − 13 ≥19 ⇔ (q− 3)2 ≥ 64 ⇒ q ≥ 11.

Следовательно, наименьшее подходящее $q = 11$ .

Ответ: 11

Ошибка.
Попробуйте повторить позже

Задача 5#2351Максимум баллов за задание: 2

В январе 2014 года процентная ставка по депозитам в банке составила $x%$ годовых, а в январе 2015 года — $y%$ годовых. Вкладчик положил на счет в этом банке в январе 2014 года некоторую сумму денег в рублях. В январе 2015 года, спустя год после открытия счета, он снял со счета пятую часть от той суммы, которую положил в 2014 году. Найдите значение $x,$ при котором сумма на счете в январе 2016 года будет наибольшей, если известно, что $x +y = 30.$

Источники: пробный ЕГЭ 2015

Показать ответ и решение

Пусть вкладчик положил на счет $A$ рублей. Тогда спустя год, то есть в 2015 году, на счете уже будет в рублях

(1+ 0,01x)A

Затем вкладчик снял со счета $1 5A,$ следовательно, на счете осталось в рублях

(1+ 0,01x)A − 1A 5

Тогда в январе 2016 года на счете будет сумма в рублях:

1 (1 +0,01y)((1+ 0,01x)A − 5A )= =(1+ 0,01y)(1+ 0,01x− 0,2)A

Выразим по условию $y = 30− x$ и рассмотрим функцию

f(x) =(1+ 0,01(30− x))(1+ 0,01x − 0,2)= 1 2 = 104 ⋅(−x +50x+ 130⋅80)

Графиком этой функции является парабола, ветви которой направлены вниз. Следовательно, наибольшее значение она принимает в вершине

−-50 x0 = −2 = 25

Таким образом, наибольшая сумма на счете в январе 2016 года будет при $x= 25.$

Ответ: 25

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Верно построена математическая модель	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Подробнее: 1 балл выставляется в тех случаях, когда сюжетное условие задачи верно сведено к решению математической (арифметической, алгебраической, функциональной, геометрической) задачи, но именно к решению, а не к отдельному равенству, набору уравнений, уравнению, задающему функцию, и т.п. Предъявленный текст должен включать описание того, как построена модель.